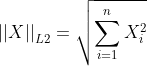知识图谱 ——距离变换模型

目录

一、模型基础

二、TransE模型

三、TransH模型

四、TransR模型

五、TransD模型

---

一、模型基础

L1范数（曼哈顿距离）与L2范数（欧氏距离）：

L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)

L1范数是指向量中各个元素绝对值之和

L2范数是指向量各元素的平方和然后求平方根

L1范数可以进行特征选择，即让特征的系数变为0.

L2范数可以防止过拟合，提升模型的泛化能力，有助于处理 condition number不好下的矩阵(数据变化很小矩阵求解后结果变化很大)

下降速度：最小化权值参数L1比L2变化的快

模型空间的限制：L1会产生稀疏 L2不会。

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。

L1计算公式：

L2计算公式：

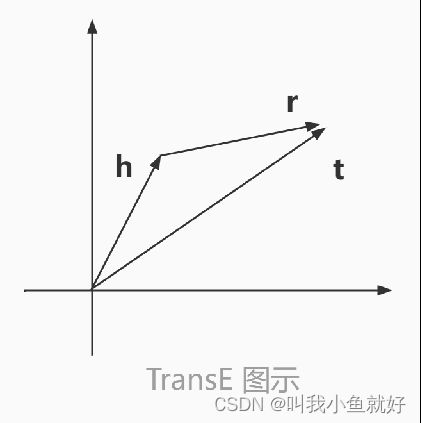
二、TransE模型

        TransE模型：将知识库中的关系看作实体间的某种平移向量。对于每个事实三元组（h，r，t），假设它们分别有向量表示h，r，t。TransE模型将实体和关系表示在同一空间中，把关系向量r看作头实体向量h和尾实体向量t之间的平移，即h+r≈t。

        例：h1+r≈t1，h2+r≈t2   =>   h1-t1 ≈ h2-t2

         由此，我们也可以将r看作从h到t的翻译，因此TransE模型也被称为翻译模型。它的打分函数可以定义为h+r与t距离的负，即 

        其中L1/L2为L1范数或L2范数。 

        理想情况下，一个正确的三元组的embedding之间会有h + r = t的关系，而错误的三元组之间不会有这个关系。 因此我们定义如下的势能函数,通过h和r之和与t之差的二范数来表示这个三元组的势能:

        对于一个正确的三元组，需选取势能较低的结果，而对于一个错误的三元组，需选取势能较高的结果。以此得到目标函数： 

        其中：∆表示正确的三元组集合，∆‘表示错误的三元组集合，γ表示正负样本之间的距离，是一个常数，通常取1，[x]+表示max(0,x) 

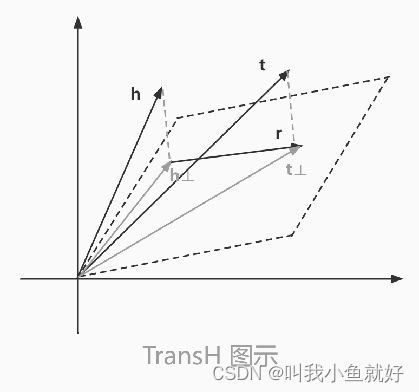
三、TransH模型

        虽然TransE模型简单高效，计算复杂度低，在大规模稀疏知识库上具有较好的性能与可扩展性，但是它不能解决多对一和一对多关系的问题。以多对一关系为例，固定r和t，TransE模型为了满足三角闭包关 系，训练出来的头节点的向量会很相似，但实体在涉及不同关系时应该具有不同的表示形式。

        TransH模型：为了解决TransE模型在处理一对多、多对一、多对多复杂关系时的局限性，TransH模型提出让一个实体在不同的关系下拥有不同的表示。对于关系r，TransH模型同时使用平移向量r和超平面的法向量wr来表示它。对于一个三元组（h，r，t），TransH模型先将头实体向量h和尾实体向量t投影到关系r对应的超平面上，分别得到h⊥和t⊥，再对投影用的TransE模型进行训练和学习。

因此，TransH模型的评分函数为：

 其中，。需要注意的是，关系r可能存在无限个超平面，TransH模型简单地令r与wr近似正交，来选取某一个超平面。TransH模型使不同的实体在不同的关系下拥有了不同的表示形式，但由于实体向量被投影到了关系的语义空间中，故它们具有相同的维度。所以，

由此，目标函数为：

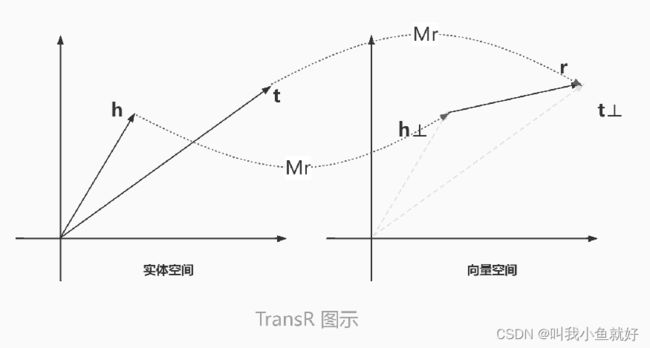
四、TransR模型

        TransR模型与TransH模型的思想类似，它引入的是关系特定的语义空间，而不是超平面。虽然TransH模型使每个实体在不同关系下拥有了不同的表示，但是它仍然假设实体和关系处于相同的语义空间中，这在 一定程度上限制了TransH模型的表示能力。TransR模型则将一个实体看作多种属性的综合体，不同的关系拥有不同的语义空间并关注实体的不同属性。

        具体而言，对于每一个关系r，TransR模型定义投影矩阵Mr，将实体向量h和t从实体空间投影到关系r对应的子空间：

        TransR模型利用和TransH模型相同的翻译关系  得到关于三元组的评分函数：

        目标函数为： 

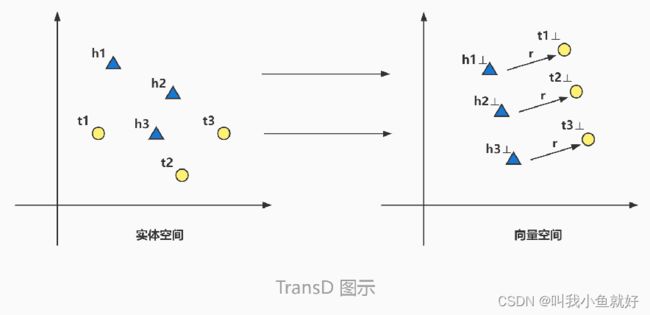
五、TransD模型

        虽然TransR模型较TransE模型和TransH模型有显著的改进，但它仍然有如下缺点：

        （1）在同一个关系下，头实体和尾实体共享相同的投影矩阵。然而，一个关系的头实体和尾实体的类型或属性可能差异巨大

        （2）从实体空间到关系空间的投影是实体和关系之间的交互过程，因此TransR模型让投影矩阵仅与关系有关是不合理的。

        （3）与TransE模型和TransH模型相比，TransR模型引入了空间投影，使得TransR模型的参数量急剧增加，计算复杂度大大提高。

 

        为了解决这些问题，TransD模型设置了两个分别将头实体h和尾实体t投影到关系空间的投影矩阵和。

 ，​​​​。

        其中，由一个对应关系的向量和一个对应头实体的向量组成，则由和一个对应尾实体的向量组成：，，这样投影矩阵就不仅和关系有关，还和被投影的实体有关系。另外，通过两个向量外积的定义方式，TransD模型可以使投影矩阵的参数变少，从而降低模型的复杂度。

 

如果能解决您的问题，记得收藏+关注呀！！！

创作时间：2022.12.22

文章编号YU.NO.7