C语言算法基础——二叉树的实现

---

---

前言

1、二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分 。
2、二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点 。

百度百科-二叉树

---

一、实现二叉树的基本思想

1、二叉树的结构其实和链表类似，一个结构体中有一个数据域和两个指针域，只不过链表是顺序的，二叉树是树状的。
2、二叉树的遍历：
(1)前序遍历：先访问根节点，再访问左节点，最后访问右节点
(2)中序遍历：先访问左节点，再访问根节点，最后访问右节点
(3)后序遍历：先访问左节点，再访问右节点，最后访问根节点
3、二叉树无论是实现还是使用，都离不开递归，递归的思想非常不好理解，而且从理解到实现还需要一个过程，需要大家多多思考。

二、二叉树的代码

1.二叉树的结构体

#include
#include
typedef struct tree_node
{
	int data;//数据域
	struct tree_node *left;//左指针
	struct tree_node *right;//右指针
}Tree_Node;

2.二叉树的初始化

初始化即创建根节点

Tree_Node *init()
{
	Tree_Node *root=(Tree_Node *)malloc(sizeof(Tree_Node));//为根节点申请地址
	root->left=NULL;
	root->right=NULL;
	root->data=0;
	return root;
}

3.二叉树的创建

构建一个二叉树，给二叉树子节点申请空间并赋值，输入-1则节点为空

Tree_Node *create(Tree_Node *root)
{
	int value;
	scanf("%d", &value);//输入当前节点的值
	if (value == -1)
	{
		root = NULL;
	}
	else
	{
		root=(Tree_Node *)malloc(sizeof(Tree_Node));//为新节点申请空间
		root->data=value;
		root->left=create(root->left);//递归左子树
		root->right=create(root->right);//递归右子树
	}
	return root;
}

4.前中后序遍历

//前序遍历
void pre_traverse(Tree_Node *root)
{
	if(root==NULL)
		return;
	printf("%-5d",root->data);//先打印数据
	pre_traverse(root->left);//递归左子树
	pre_traverse(root->right);//递归右子树，下面的同理
}
//中序遍历
void mid_traverse(Tree_Node *root)
{
	if(root==NULL)
		return;
	mid_traverse(root->left);
	printf("%-5d",root->data);
	mid_traverse(root->right);
}
//后续遍历
void aft_traverse(Tree_Node *root)
{
	if(root==NULL)
		return;
	aft_traverse(root->left);
	aft_traverse(root->right);
	printf("%-5d",root->data);
}

5.求树的深度

二叉树的深度是指二叉树的所有结点中最深的结点所在的层数。
举个例子：
1、一颗树只有一个节点，它的深度是1；

2、二叉树的根节点只有左子树而没有右子树，那么可以判断，二叉树的深度应该是其左子树的深度加1；

3、二叉树的根节点只有右子树而没有左子树，那么可以判断，那么二叉树的深度应该是其右树的深度加1；

4、二叉树的根节点既有右子树又有左子树，那么可以判断，那么二叉树的深度应该是其左右子树的深度较大值加1。

int get_height(Tree_Node *root)
{
	int lh=0,rh=0;//lh左子树的深度，rh右子树的深度
	if(root==NULL)
		return 0;
	lh=get_height(root->left);//左子树递归
	rh=get_height(root->right);//右子树递归
	return 1+(lh>rh?lh:rh);//？:表达式，如果lh>rh返回lh，否则返回rh
}

6.二叉树的翻转

翻转二叉树

void reverse_tree(Tree_Node *root)
{
	if (root != NULL)
    {
		Tree_Node *s;
        s = root->left;
        root->left = root->right;
        root->right = s;
        reverse_tree(root->left);
        reverse_tree(root->right);
    }
}

7.主函数测试

主函数：创建树，翻转后输出前中后序遍历

int main()
{
	Tree_Node *root=init();
	root=create(root);//创建树
	reverse_tree(root);//翻转树
	printf("previous traverse output:\n");
	pre_traverse(root);
	printf("\nmiddle traverse output:\n");
	mid_traverse(root);
	printf("\nafter traverse output:\n");
	aft_traverse(root);
	printf("\n");
}

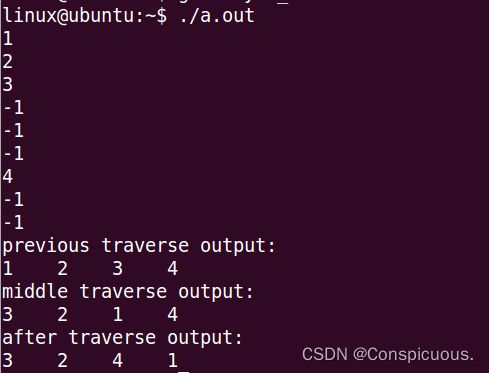
8.结果展示

输入的树：

未翻转前：

翻转后：

---

总结

今天就不总结了……