python求方差_【金工基础7】在险价值(VaR)的Python实现

大家好，这篇文章给大家带来在险价值(Value at Risk)的内容。

金融学的核心就是风险和收益，如何在风险可控的条件下尽可能的扩大收益，或如何在稳定收益的前提下尽量降低风险。著名学者，诺贝尔经济学奖得主、哈佛大学金融学教授罗伯特·莫顿说：金融学是一门研究人们在不确定环境下如何进行稀缺资源(资金)跨时间配置的学科。

如何度量风险呢。风险测度主要关注市场风险，信用风险和流动性风险。本文提到的在险价值就是衡量市场风险的一个方法。

在险价值VaR又叫做在险价值量，是指在正常市场环境下，你投资的项目可能遭受的最大损失。比如，99%的置信水平的VaR为100元，那么也就是说损失超过100万元的概率为1%。反过来说，可以说有99%的把握确定损失不会超过100万元。

用概率来描述的话

其中，表示未来可能的损失，表示在险价值，表示置信水平。

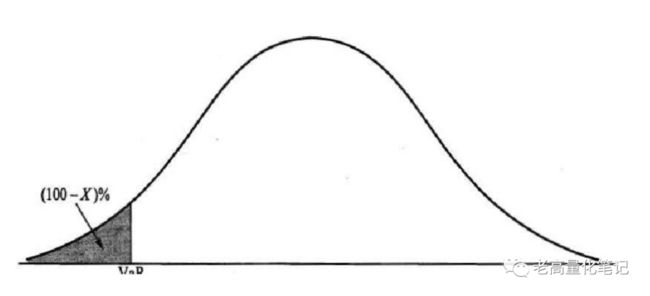
用分布来表示(图片来源网络，侵删)

从图中可以看出，实际上就是分布的分位数

一、单个资产的VaR计算方法

其中为初始投资额，为预期收益率，为预期波动率，表示标准正态分布的分位数，即

下面，我们用Python计算一下。

def Single_Asset_VaR(W0, mu, sigma, alpha=0.95):
    '''
    单个资产的VaR值
    Parameters
    ----------
    W0: -> float 初始资产
    mu: -> float 预期收益率
    sigma: -> float 预期波动率
    alpha: -> float 置信水平
    Return
    ------
    VaR: -> float 在险价值量
    '''
    Z = scipy.stats.norm.ppf(1-alpha)
    VaR = W0 * (mu + sigma * Z)
    return VaR

假设，投资总额为100万元，投资期望收益率为12%，投资收益率标准差为5%，求在98%的置信水平下投资的VaR是多少？

W0 = 100.0
mu = 0.12
sigma = 0.05
alpha = 0.98
VaR1 = Single_Asset_VaR(W0, mu, sigma, alpha)
print(VaR1)
# 1.731255446840886

二、投资组合的VaR值计算方法

投资组合的VaR值计算方法主要有三种，方差-协方差法，历史模拟法和蒙特卡洛法。

1.方差-协方差法

方差-协方差法又称为模型构建法，是最常用的方法。

我们首先按各个资产收益率序列计算出相关系数矩阵，如果手动给出也可以。然后我们根据预期收益和证券的投资比例计算出投资组合的预期收益，然后再根据预期波动率构造方差协方差矩阵，然后与相关系数矩阵相乘得到预期波动率。

我们可以用Python来实现。

def Cov_VaR(W0, data, mu, sigma, percentage, alpha=0.95):
    '''
    资产组合的VaR计算方法(方差协方差)
    Parameters
    ----------
    W0: -> float 初始投资额
    data: -> DataFrame 证券的收益率数据
    mu: -> np.ndarray 证券预期收益率
    sigma: -> np.ndarray 证券预期波动率
    percentage: -> list 证券权重
    alpha: -> float 置信水平
    Return
    ------
    VaR: -> float 资产组合的在险价值
    '''
    rho = data.corr().values
    std = np.diag(sigma)
    cov = np.dot(std, np.dot(rho, std))
    mu = (mu * np.array(percentage)).sum()
    sigma = np.dot(np.array(percentage), np.dot(cov, np.array(percentage).reshape(-1, 1)))
    Z = Z = scipy.stats.norm.ppf(1-alpha)
    VaR = W0 * (mu + sigma * Z)
    return VaR    

我们可以尝试计算一下

codelist = ['601398.SH', '601601.SH', '601390.SH']
startdate = '2020-01-01'
enddate = '2020-06-01'
data = get_stock_data(codelist, startdate, enddate)
W0 = 100.0
mu = np.array([0.06, 0.15, 0.09])
sigma = np.array([0.041, 0.0534, 0.0583])
percentage = [0.4, 0.3, 0.3]
VaR2 = Cov_VaR(W0, data, mu, sigma, percentage)
print(VaR2)

2.历史模拟法

历史模拟法就是以历史数据为依据，通过已经实现的收益率和市场价值变化来模拟下一期的市场价值变化，从而计算出风险价值。历史模拟发的前提假设是历史数据在将来可能重演。

第一步：选择一定时间段内影响资产或组合的历史收益率的时间序列 第二步：采用实际价格计算未来一天的变化可能。第三步：利用变化构造出概率分布，然后求出分位数。

下面，我们用Python来进行计算。

def History_VaR(W0, data, current_price, percentage, alpha=0.95):
    '''
    利用历史模拟法计算VaR值
    Parameters
    ----------
    W0: -> float 初始投资额
    data: -> DataFrame 历史收益率
    current_price: -> np.ndarray 当前价格
    percentage: -> list 证券的投资比例
    alpha: -> float 置信水平
    Returns
    -------
    VaR: -> float 在险价值
    '''
    his_return = data.values / 100
    price_future = current_price * (his_return + 1)
    returns_future = np.sum((W0 * np.array(percentage)) * his_return, axis=1)
    Z = int((1-alpha) * returns_future.shape[0])
    VaR = -np.sort(returns_future)[Z]
    return VaR

我们计算一下实际的风险价值

codelist = ['601398.SH', '601601.SH', '601390.SH']
startdate = '2020-01-01'
enddate = '2020-06-01'
data = get_stock_data(codelist, startdate, enddate)
current_price = get_stock_data(codelist, startdate, enddate, field='close').values[-1]
W0 = 100.0
percentage = [0.4, 0.3, 0.3]
VaR3 = History_VaR(W0, data, current_price, percentage)
print(VaR3)

3.蒙特卡洛法

历史模拟法师用历史数据来模拟计算风险价值，是以证券价格的历史数据为基础，直接计算股票价格的变动率来得到每期的绝对收益，并以历史数据的最坏情况来确定投资组合的风险价值。但是问题在于，历史的数据不一定能完全代表。而蒙特卡洛法师结合了方差协方差方法和历史模拟发，通过模拟随机数组构建一个未来价格的变化路径，利用产生的随机价格通过历史模拟法的计算方法来计算投资组合的在险价值。

我们用一下的随机过程来模拟股票价格

其中，表示期望收益率，表示波动率，为时间间隔，若和表示年收益率的期望和波动率，则天的时间间隔表示为。若和为日收益率的期望和波动率，则天的时间间隔表示为。

然后用该过程模拟出个价格，利用这个可能的价格来计算投资组合的价值变化，然后结合历史模拟法就可以了。

下面，我们用Python来实现。

def MC_VaR(W0, current_price, percentage, mu, sigma, n, alpha=0.95):
    '''
    Parameters
    ----------
    W0: -> float 初始投资额
    current_price: -> np.ndarray 今日价格
    percentage: -> list 投资比例
    mu: -> np.ndarray 期望收益率
    sigma: -> np.ndarray 期望波动率
    n: -> int 模拟次数
    alpha: -> float 置信水平
    Returns
    -------
    VaR: -> float 在险价值
    '''
    price_sim = current_price * np.exp((mu - np.square(sigma)/2 + sigma*np.random.randn(n,mu.shape[0])))
    pct_chg_sim = price_sim / current_price - 1
    returns_sim = np.sum((W0 * np.array(percentage)) * pct_chg_sim, axis=1)
    Z = int((1-alpha) * returns_sim.shape[0])
    VaR = -np.sort(returns_sim)[Z]
    return VaR

我们还是拿上面的股票进行测试

codelist = ['601398.SH', '601601.SH']
startdate = '2020-01-01'
enddate = '2020-06-01'
current_price = get_stock_data(codelist, startdate, enddate, field='close').values[-1]
W0 = 100.0
mu = np.array([0.03, 0.01])
sigma = np.array([0.05, 0.06])
percentage = [0.4, 0.6]
n = 1000
VaR4 = MC_VaR(W0, current_price, percentage, mu, sigma, n)
print(VaR4)

好了，本期的内容就到这里了，如果对你有帮助，麻烦点个"在看"喔！

到这里，南开的金工的内容就全部结束了，接下来我将参考人大的金数和郑振龙的《金融工程》将这个专辑的内容补充完整。