基于隐马尔科夫模型的图像质量评估模型
先占座
第一章 马尔科夫模型概述
首先,这部分的较少网上大家转载了好多次了,我已经找不到具体的出处了。
我参考的是这个大牛的博客:https://www.cnblogs.com/zhizhan/p/4161516.html
1.1 马尔科夫链
如下图的马尔科夫模型状态转移

图中的方框代表你要建模过程的可能状态,箭头表示状态间的转移情况。箭头上的标签表示转移概率。在过程中的每一步,模型会产生一个输出(决定于所处的状态)然后转移到另一个状态。马尔科夫模型的一个重要特性是下一个状态只与当前的状态有关,与过去的转移无关。
例如,对于一个顺序抛掷硬币的过程,存在两个状态:正和反。最近一次的投掷决定了模型当前的状态,下一次投掷决定了如何转移到下一状态。如果硬币是公平的,则转移概率都是二分之一,输出就是当前的状态。在更复杂的模型中,每一个状态可以以一个随机过程产生输出,如可以通过投掷骰子来决定输出。
马尔科夫链是离散状态马尔科夫模型的数学描述。马尔科夫链如下定义:
A 一系列状态{1,2,…,M};
B 一个MXM的状态转移矩阵T,其中Tij表示从状态i到j的状态转移概率。矩阵每行的和为1,因为它表示从一个给定状态到其他各状态的所有转移概率的和。
C一系列可能的输出 s 1 , s 2 , … , s N {s_{1},s_{2},…,s_{N}} s1,s2,…,sN,默认时可以当做{1,2,…,N},N为可能输出的个数,当然你可以选择不同的数据集或符号来表示;
D 一个MXN的输出矩阵E,其中 E i k E_{ik} Eik表示模型在状态 i i i时的输出 s k s_{k} sk的概率。
马尔科夫链的过程:从第0步的初始状态 i 0 i_{0} i0开始;然后以概率 T i 1 T_{i1} Ti1转移到状态i1,并以概率 E i 1 k 1 E_{i1k1} Ei1k1输出 s k 1 s_{k1} sk1;最后,以概率 T i 1 T_{i1} Ti1、 E i 1 k 1 E_{i1k1} Ei1k1 T i 1 i 2 T_{i1i2} Ti1i2 E i 2 k 2 E_{i2k2} Ei2k2 … T i r − 1 i r T_{ir-1ir} Tir−1ir E i r k E_{irk} Eirk观察到状态 i 1 , i 2 … i r i1, i2…ir i1,i2…ir,同时输出 s k 1 s_{k1} sk1, s k 2 s_{k2} sk2… s k r s_{kr} skr。
1.2 隐马尔科夫模型(HMM)
隐马尔科夫模型是你只观察到输出,但不知道模型产生输出所经历的状态。隐马尔科夫模型分析就是从观察的数据恢复相关的状态序列。
例如,考虑一个有2个状态6个可能输出的马尔科夫模型,模型中用到
一个红骰子,6个面,分别标号1~6;
一个绿骰子,12个面,5个面标号2~6,其他面标记1;
一个非均衡的红硬币,以0.9的概率掷出正,0.1的概率掷出反;
一个非均衡的绿硬币,以0.95的概率掷出正,0.05的概率掷出反。
模型以下面的规则产生一系列来自{1,2,3,4,5,6}的数字序列:
先掷红骰子,记下骰子的输出;
然后掷红硬币:
如果是正,则掷红骰子记下结果;
否则掷绿骰子记结果;
接下来的下一步,掷与上一步所用骰子同颜色的硬币,如果是正,则掷同颜色的骰子;否则掷另一个骰子。
模型的状态转移图如下:
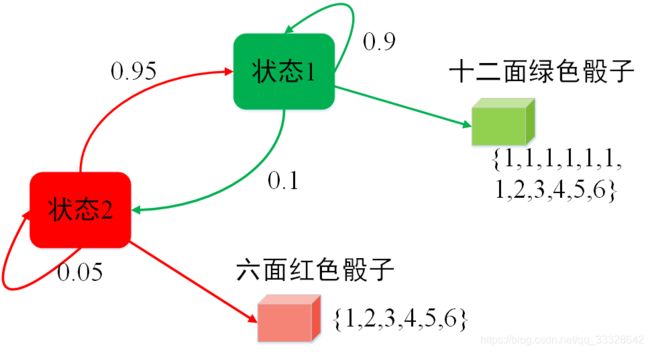
这个模型中,通过掷与状态同颜色的骰子来决定输出,通过掷与状态同颜色的硬币来决定转移到哪一状态。
输出矩阵为

这个模型是非隐的,因为你从硬币、骰子的颜色可以知道状态序列。如果假设有人产生了一系列输出,但不给你展示硬币和骰子,所有你能看到的只是输出序列。如果你开始看到1出现的次数比其他都多,你可能会假设模型处于绿状态,但你不能确定,因为你不能看到所掷骰子的颜色。
隐马尔科夫模型提出了如下问题:
-
给定输出序列,求最可能的状态序列? -
给定输出序列,你如何估计模型的转移概率和输出概率? -
模型得出给定序列的先验概率? -
模型在序列某一位置是特定状态的后验概率?
1.3 隐马尔科夫模型的matlab工具箱
与隐马尔科夫模型有关的统计工具箱函数如下
l . Hmmgenerate——从一个马尔科夫模型产生状态、输出序列;
lI. Hmmestimate——从输出序列和已知的状态序列计算转移、输出序列概率的极大似然估计;
lII . Hmmtrain——从输出序列计算转移、输出序列概率的极大似然估计;
lV. Hmmviterbi——计算隐马尔科夫模型的最大可能状态序列;
Vl . Hmmdecode——计算输出序列的状态后验概率。
下面来讲如何使用这些函数分析隐马尔科夫模型。
1.3.1 产生测试序列
下面的命令创建状态转移矩阵和输出矩阵
TRANS = [0.9 0.1; 0.05 0.95;];
EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;…
7/12, 1/12, 1/12, 1/12, 1/12, 1/12];
要产生一组状态和输出的随机序列,使用函数hmmgenerate
[seq,states] = hmmgenerate(1000,TRANS,EMIS);
输出参数seq为输出序列,states为状态序列。
在matlab上的仿真结果如下:
上述两个矩阵都是1*N的向量,为了方便大家观察,我们这两个矩阵在matlab中reshape成方阵,这样就能方便观察两个矩阵的数据了。
代码如下:
clc
clear all
close all
TRANS = [.9 .1; .05 .95;];
EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;...
7/12, 1/12, 1/12, 1/12, 1/12, 1/12];
%要产生一组状态和输出的随机序列,使用函数hmmgenerate
[seq,states] = hmmgenerate(1000,TRANS,EMIS);
a=reshape(seq,20,50);
b=reshape(states,20,50);
运行矩阵的截图如下:
a就是这个仿真结果的最终输出序列,因为骰子的输出只有1-6这六个数,所以输出只有这几个数
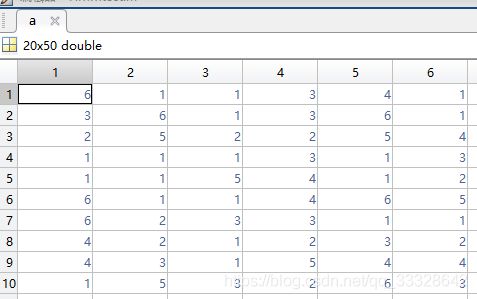
b是我们的状态序列,因为只有红色和绿色两状态,分别用1和2表示,因此输出只是在这两个状态之间转换,因此只有1和2两个数字。

Hmmgenerate函数第0步开始于状态1,然后第一步转移到状态i1,而i1作为states的第一个元素。如果要改变初始状态,看后面的改变初始状态分布一节。
1.3.2 估计状态序列
给定状态转移矩阵TRANS和输出矩阵EMIS,函数hmmviterbi使用Viterbi算法计算产生给定输出序列seq的极大可能状态序列
likelystates = hmmviterbi(seq, TRANS, EMIS);
likelystates与seq长度相同。
为了测试hmmviterbi的精确度,计算实际状态序列states与估计状态序列likelystates吻合的百分比
sum(states==likelystates)/1000
ans =0.8200
在这个例子中,估计的状态和实际吻合达82%
这个我们还是要给出matlab的代码的,我想跟大家表达的是一个什么样的东西呢?
简单的说就是我们要知道每一步的转移概率,而不是平均的,这对我们来讲意义不大,或者说对我下面要讲的意义不大。
1.3.3 估计状态转移矩阵和输出矩阵
函数hmmestimate和hmtrain可以用来根据给定的输出序列估计状态转移矩阵和输出矩阵。
使用hmmestimate
此函数需要你知道产生输出序列的状态序列。基于输出序列和状态序列,如下估计转移矩阵和输出矩阵
[TRANS_EST, EMIS_EST] = hmmestimate(seq, states)
TRANS_EST =
0.8989 0.1011
0.0585 0.9415
EMIS_EST =
0.1721 0.1721 0.1749 0.1612 0.1803 0.1393
0.5836 0.0741 0.0804 0.0789 0.0726 0.1104
与原始的序列对比
TRANS =
0.9000 0.1000
0.0500 0.9500
EMIS =
0.1667 0.1667 0.1667 0.1667 0.1667 0.1667
0.5833 0.0833 0.0833 0.0833 0.0833 0.0833
1.3.4 使用hmmtrain
如果你不知道状态序列,但知道TRANS和EMIS矩阵的初始猜测(PS:这个矩阵,在我们以后的项目中,我们将编写一个引导模型生成多个近似的序列来作为初始猜测矩阵),可以使用hmmtrain函数估计。
假设已知TRANS和EMIS矩阵的初始猜测如下
TRANS_GUESS = [0.85 0.15; 0.1 0.9];
EMIS_GUESS = [0.17 0.16 0.17 0.16 0.17 0.17;0.6 0.08 0.08 0.08 0.08 0.08];
下面做矩阵估计
[TRANS_EST2, EMIS_EST2] = hmmtrain(seq, TRANS_GUESS, EMIS_GUESS)
TRANS_EST2 =
0.2286 0.7714
0.0032 0.9968
EMIS_EST2 =
0.1436 0.2348 0.1837 0.1963 0.2350 0.0066
0.4355 0.1089 0.1144 0.1082 0.1109 0.1220
Hmmtrain函数使用迭代算法调整TRANS_GUESS和EMIS_GUESS,使得基于调整的矩阵产生更加类似于观察序列seq的输出。当两次迭代中矩阵的变化不大时迭代结束。
如果如果算法在默认的最大迭代次数100次以内仍没结束,将返回迭代的最后结果并产生一个警告。这时可以通过增加最大迭代次数来增大迭代的次数
hmmtrain(seq,TRANS_GUESS,EMIS_GUESS,‘maxiterations’,maxiter)
maxiter是新设的最大迭代次数。
还可以改变默认的最小容忍值
hmmtrain(seq, TRANS_GUESS, EMIS_GUESS, ‘tolerance’, tol)
tol为新设的最小容忍值,增大它可以让算法更快的停止,但结果将不精确。
两个因素将降低hmmtrain函数估计结果的可靠性:
l 算法收敛到一个局部极大值,但此极大值并不是真正的状态转移矩阵与输出矩阵的位置。对此,可以使用多个不同的初始猜测值来估计,使用最好的结果;
l Seq序列太短,以至于不足以训练矩阵,对此,可以使用更长的seq序列。
1.3.5 估计后验状态概率
输出序列seq的后验状态概率是模型给出seq序列时所处状态的后验概率。可以使用hmmdecode函数计算后验状态概率:
PSTATES = hmmdecode(seq,TRANS,EMIS)
随着序列长度的增加,序列的概率会趋向于0,所以一个足够长的序列的概率将小于计算机的最小精度,为了避免此问题,hmmdecode还返回了概率的对数值。
1.3.6 改变初始状态分布
默认地,统计工具箱的隐马尔科夫模型函数是从状态1开始的。换句话说,初始状态的分布集中在状态1处,其他位置为0。如果想给初始状态赋予一个概率分布p=[p1,p2,…,pM],可以如下实现
创建一个M+1XM+1的辅助状态转移矩阵如下
其中的T是真正的状态转移矩阵,第一列包含M+1个0,向量p的和为1。
创建M+1XN的辅助输出矩阵如下
如果状态转移矩阵与输出矩阵式TRANS和EMIS,可以使用如下命令创建辅助矩阵
TRANS_HAT = [0 p; zeros(size(TRANS,1),1) TRANS];
EMIS_HAT = [zeros(1,size(EMIS,2)); EMIS];
第二章 基于…全局像素质量计算
待续…
第三章 基于马尔科夫模型的图像质量评估
待续…论文投稿中…
