matlab hull white,Matlab通过市场数据校准Hull-White利率模型参数
ans =
21-Mar-2008
21-Jun-2008
21-Sep-2008
21-Dec-2008
21-Mar-2009
21-Jun-2009
21-Sep-2009
21-Dec-2009
21-Mar-2010
21-Jun-2010
21-Sep-2010
21-Dec-2010
21-Mar-2011
在最佳情况下,查找带有Strike =的 市场波动率 0.0690,以及列出的到期日,但找到这些确切数据的可能性很小。结果,使用市场上可用的数据并进行插值。
根据市场数据,您可以获得不同日期和行使价的上限信息。
到期协议1 = 0.0590协议2 = 0.07902008年3月21日0.15330. 15262008年6月21日0.17310. 17302008年9月21日0. 17270. 17262008年12月21日0. 17520. 17472009年3月21日0. 18090. 18082009年6月21日0. 18090. 17922009年9月21日0. 18050. 17972009年12月21日0.18020. 17942010年3月21日0.18020. 17332010年6月21日0. 17570. 17512010年9月21日0. 17550. 17502010年12月21日0. 17550. 17452011年3月21日0. 17260. 1719
要求日期,协议价和实际波动分为三个变量: MarketStrike, MarketMat,和 MarketVol。
MarketStrike = [0.0590; 0.0790];
MarketMat = {'21-Mar-2008';
'21-Jun-2008';
'21-Sep-2008';
MarketVol = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802 0.1735 0.1757 ...
使用此数据完成输入参数 RateSpec:
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [14x1 double]
Rates: [14x1 double]
EndTimes: [14x1 double]
StartTimes: [14x1 double]
EndDates: [14x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1
调用校准例程以找到波动率参数Alpha和Sigma的值
根据市场数据计算的值 Alpha ,Sigma 。例如,您可以将目标函数的公差定义为 100*eps :
Local minimum possible.
> In hwcalbycapfloor at 93
In hwcalbycap at 75
Alpha =
1.0000e-06
Sigma =
0.0127
先前的警告表明转换不是最佳的。使用的搜索算法未找到符合所有约束的解决方案。要辨别该解决方案是否可接受,请通过为以下项指定第三个输出(OptimOut)来查看 优化结果:
hwcalb(RateSpec, MarketStrike, MarketMat,...
结构的 OptimOut.residual 字段 OptimOut是优化残差。此值包含Black caplet和优化过程中计算出的值之间的差异。您可以使用该 OptimOut.residual 值计算与Black Caplet价格相比的百分比差异(误差),然后确定残差是否可以接受,决定是否接受以单一数值参数化的市场 Alpha 和 Sigma。
使用市场数据和Black模型获取价格
Black -76模型被认为是世界范围内广泛接受的互换期权定价模型,互换期权计算公式看起来和期权价格公式一 样,这表示在使用Black模型对互换期权进行定价时,可以用和定价期权时同样的方法进行计算.为了使Black模型生效,只需输入由市场决定的隐含波动率即可。
为了确定优化的有效性,请使用Black公式和市场数据计算参考值。请注意,您必须首先对市场数据进行插值以获得用于计算的数据量:
FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity),
使用Black模型计算价格:
capbybike, Settle, Maturity, FlatVol,...
Caplets =
0.3210
1.6355
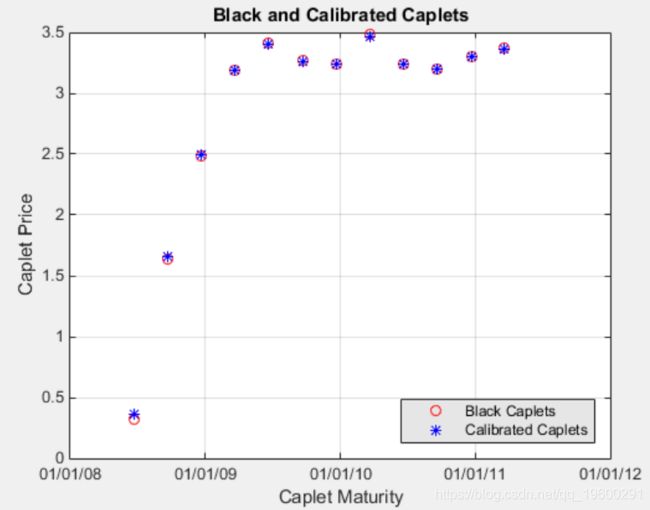
比较优化值和Black值并以图形方式显示
在计算了参考值之后,请通过分析和图形方式比较这些值,以确定是否计算出的单个值 Alpha 并 Sigma 提供适当的近似值:
plot(MarketMatNum(2:end), Caplets, 'or', MarketMatNum(2:end), O
ylabel('Caplet Price');
t
set(gcf, 'NumberT
使用Black,HW分析和HW树模型比较上限价格
最受欢迎的见解
1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用
2.R语言GARCH-DCC模型和DCC(MVT)建模估计
3.R语言实现 Copula 算法建模依赖性案例分析报告
4.R语言COPULAS和金融时间序列数据VaR分析
5.R语言多元COPULA GARCH 模型时间序列预测
6.用R语言实现神经网络预测股票实例
7.r语言预测波动率的实现:ARCH模型与HAR-RV模型
8.R语言如何做马尔科夫转换模型markov switching model
9.matlab使用Copula仿真优化市场风险
使用Black模型,Hull-White分析模型和Hull-White树模型比较相应上限价格。