（9.1）Dijkstra算法

一、Dijkstra算法特点：

Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径集。

二、Dijkstra算法原理：

Dijkstra算法采用的是一种贪心的策略，利用一个集合openlist来保存原点到各个顶点的最短距离和一个closelist集来保存已经找到的最短路径的集合。

一开始openlist中只有起始点S，且它的路径权重node_cost为0。将S点放入closelist中，然后将S的相邻节点放入openlist中。

A*算法的流程步骤为：

①、将起始点加入openlist中；

②、重复下面的过程：

        1、遍历openlist，查找node_cose值最小的节点，把它当作当前要处理的节点current_node；

        2.把这个节点加入closelist表中；

        3、对当前节点的相邻节点处理如下（对于二维平面可以选择只有直线运动的4个方向或者带

         对角线运动的8个方向）：

• a、如果它是障碍点或不可达点（边界外点）或在closelist中，忽略它；
• b、如果它不在openlist中，把它加入openlist中，并且把当前方格设置为它的父节点，记录它的node_cost值；
• c、如果它已经在openlist中，则说明已经有父节点可以到达这个点，则需要看通过当前节点到达它是否是更好的路径，比较node_cost是不是不原来小。如果更好，则将它的父节点设置为当前节点，并更新其node_cost值；如果openlist中是按node_cost大小排序则更改了节点的node_cost后需要重新排序；

        4、停止：当终点加入到了openlist中，或者查找失败，并且openlist是空的，此时没有路径；

        5、保存路径，从终点开始，每个方格沿着父节点移动到起点，便是路径；     

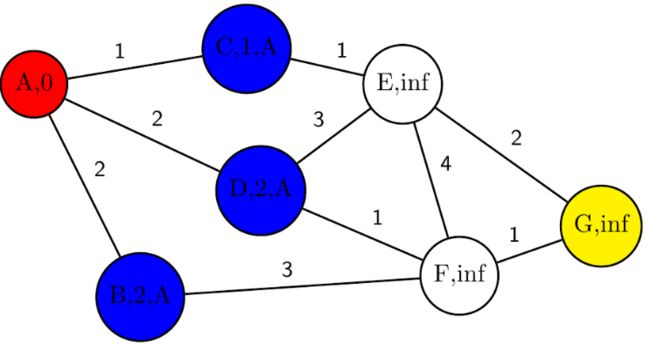
下面以一个图示说明一下（绿色代表起点，黄色代表终点，红色表示已放入closelist中，蓝色表示在openlist中，白色表示还没有遍历到）：

 

 ①、按照步骤流程，一开始openlist中只有A节点，所以遍历openlist时只得到了A，并且它的node_cost=0；然后将A加入到closelist中，并从openlist中删除，将A设置为当前节点current_code；

②、由图知A的相邻节点有三个，B、C、D，他们都不在closelist中（且不是障碍点或边界外点），他们的node_cost分别为2、2、1；所以将他们加入openlist中并且父节点为A；

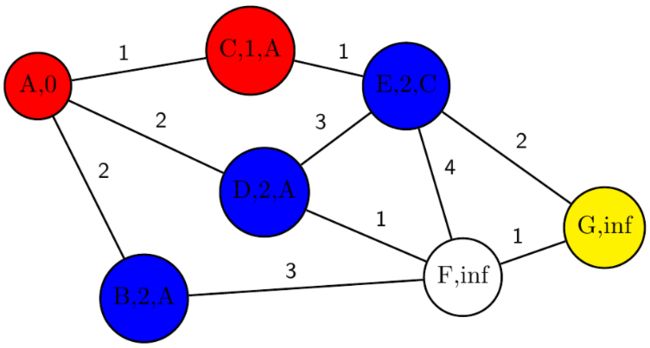
 ③、再次遍历openlist，得到node_cost最小的节点为C，将C加入closelist中；并将它从openlist中删除，将C设置为当前节点current_code；C的邻点只有E，E不在closelist中，其到C的node_cost为1，将E的node_cost更新为E到A的node_cost值（C到A的加上E到C的），并将其父节点设置为C，然后将其加入openlist中，如下图示：

 ④、第三次遍历openlist，找到node_cost最小的节点（由于这里BDE三个节点的node_cost都一样则根据排序结果会取出一个，这里假设取出的为B）；将B设置为当前节点current_code；B节点的相邻节点为F，F到B的node_cost为3，F不在closelist中，故将F加入到openlist中并更新它的node_cost值，将B设置为它的父节点；

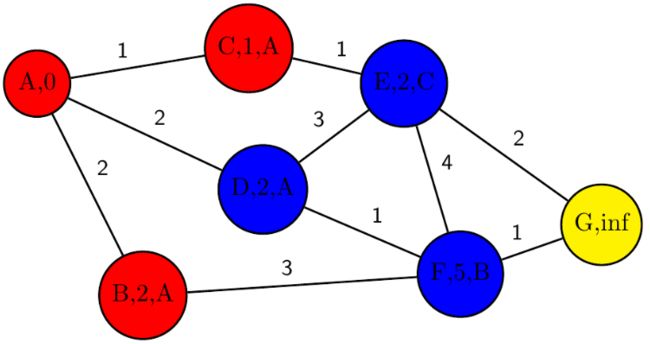
 ⑤、第四次遍历openlist，找到node_cost最小的节点D（由于D和E的node_cost相同，这里假设为D）将C加入closelist中；并将它从openlist中删除，将D设置为当前节点current_code；D的相邻节点有A、E、F，而A已经在closelist中故忽略；E和F已经在openlist表中，所以需要判断经当前节点D到他们的路径是否更优，由图可知由D到E则E到A的node_cost=4>2非更优，而由D到F则F到A的node_cost=3<5更优，所以需要将F的父节点改为D，node_cost改为3；如下图所示：

 ⑥、第五次遍历openlist，找到node_cost最小的节点E，将E加入closelist中；并将它从openlist中删除，将E设置为当前节点current_code；E的相邻节点为F和G，G不在closelist中故将其node_cost更新，父节点设置为E然后加入openlist中；F节点在openlist中需要判断当前节点到它是否是更优的，由E到F则F到A的code_cost=6>3,所以不是最优，故F不做改变；

 ⑦、第六次遍历openlist，发现终点G已经在openlist表中，故将其加入closelist中；然后结束遍历；

⑧、根据得到的closelist由终点开始通过父节点溯源，得到所求的最优路径；

 注意：在栅格化的地图中，每个节点之间的距离即node_cost是相同的；

三、实例：

这里贴出一个二维栅格地图寻优路径的例子：

clc;
clear;
close all;
%% load obs
obs = load('obsdata.txt'); %文件中的点便是障碍物
numofobs = length(obs(:,1));
%% set up color map for display 
cmap = [1 1 1; ...% 1 - white - 空地
        0 0 0; ...% 2 - black - 障碍 
        1 0 0; ...% 3 - red - 已搜索过的地方
        0 0 1; ...% 4 - blue - 下次搜索备选中心 
        0 1 0; ...% 5 - green - 起始点
        1 1 0];...% 6 - yellow -  到目标点的路径 
colormap(cmap); 
map = zeros(25); 
% 设置障碍
for j=1:numofobs
    xobs(j) = obs(j,1);
    yobs(j) = obs(j,2);
    map(xobs(j),yobs(j)) = 2;  %建立所有障碍点
end
map(1,25) = 5; % 起始点
map(25,1) = 6; % 目标点
image(1.5,1.5,map);
grid on;
axis image;
%% 
nrows = 25; 
ncols = 25; 
start_node = sub2ind(size(map), 1, 25);
dest_node = sub2ind(size(map), 25, 1);

% Initialize distance array 
distanceFromStart = Inf(nrows,ncols);  %创建一个值为无穷大的矩阵
distanceFromStart(start_node) = 0;
% For each grid cell this array holds the index of its parent 
parent = zeros(nrows,ncols); 
t0=clock; %当前时间
% Main Loop 
while true 
 % Draw current map 
 map(start_node) = 5; 
 map(dest_node) = 6; 
 image(1.5, 1.5, map); 
 grid on; 
 axis image; 
 drawnow;  %更新图窗实时显示
  % Find the node with the minimum distance 
 [min_dist, current] = min(distanceFromStart(:));%找到distanceFromStart中值最小的元素min_dist及其编号current
  if ((current == dest_node) || isinf(min_dist))  %最小值为无穷大或最小值为终点则结束
       break; 
  end; 

 map(current) = 3;  %标志为已搜索
 distanceFromStart(current) = Inf;  %已搜索过的点设置为无穷大
 [i, j] = ind2sub(size(distanceFromStart), current); %返回数组的下标
 neighbor = [i-1,j;... 
            i+1,j;... 
            i,j+1;... 
            i,j-1]; %一个矩阵元素的相邻四个元素的下标；注意对于矩阵边界上的元素其相邻元素会有不存在的情况，即下标超出数组边界
outRangetest = (neighbor(:,1)<1) + (neighbor(:,1)>nrows) +...
                   (neighbor(:,2)<1) + (neighbor(:,2)>ncols );
locate = find(outRangetest>0);
neighbor(locate,:)=[]; %去掉不在矩阵范围内的元素
neighborIndex = sub2ind(size(map),neighbor(:,1),neighbor(:,2));  %得到相邻元素的索引
for i=1:length(neighborIndex) 
if (map(neighborIndex(i))~=2) && (map(neighborIndex(i))~=3 && map(neighborIndex(i))~= 5) 
    map(neighborIndex(i)) = 4; 
  if distanceFromStart(neighborIndex(i))> min_dist + 1  
      %如果到起始点的距离大于当前的最小值加1则替换
        distanceFromStart(neighborIndex(i)) = min_dist+1; 
        %display(distanceFromStart);
        parent(neighborIndex(i)) = current; 
        %display(parent);
  end 
 end 
end 
end
TimeCost=etime(clock,t0)
display(distanceFromStart);
%distanceFromStart矩阵存放的是当前点到起始点的步数
display(parent);
%parent矩阵存放的是能到当前点的上一个点的索引值
%%
if (isinf(distanceFromStart(dest_node))) 
    route = []; 
else 
    %提取路线坐标
   route = [dest_node]
      while (parent(route(1)) ~= 0) 
              route = [parent(route(1)), route]; 
      end 
      %display(route);
  % 动态显示出路线     
        for k = 2:length(route) - 1 
          map(route(k)) = 7; 
                pause(0.1); 
                image(1.5, 1.5, map); 
              grid on; 
              axis image; 
              end 
end
axis off;  

代码中判断搜索结束的语句为：

即从openlist中搜索到了终点；则结束路径搜索，说明得到了最优路径； （这里需要注意，前面我们说只要终点出现在openlist中则结束搜索，这里是在openlist中搜索到了终点则结束搜索；两种结束方法都可以得到路径，后一种时间上可能会延长，如果openlist中还有node_cost更小的节点的话会继续搜索。实际中建议采用第一种方法结束搜索。）

从这里可以看出当当前节点为终点的父节点时，会将当前节点信息放到closelist表的终点位置上；所以在查closelist表时在终点位置上得到的是其父节点的信息； 

实际代码参见网盘：链接：https://pan.baidu.com/s/1igwHA8lSBRmFsZ-d9_viQg

提取码：49k0

四、代码说明：

1、sub2ind函数说明：

  将数组下标转换为线性索引，

语法：

ind = sub2ind（sz,row,col）--针对二维数组

ind = sub2ind(sz,I1,I2,...In) ----针对多维数组

说明：

sz为数组大小（sz(1)为行，sz(2)为列），row为行小标，col为列下标；

示例：

在3×3矩阵中指定行下标和列下标，将下标转换为线性索引。

ind2sub则与其相反是将线性索引转换为下标；

2、min()函数说明：

返回向量的最小值，及其所在的索引；

 这里数组的（:）将其变为了一个按列排放的向量如：