【机器人算法】机器人动力学、运动学和基于动力学模型的仿真与控制

---

本篇博客主要是从机器人学入门出发，以二连杆机构为例，对机器人运动学，动力学和控制进行说明。既是复习也算是科普。

因此都只给出结果，有问题欢迎评论私信。

---

运动学

运动学部分比较简单，本篇博文是基于DH参数进行建模的，二连杆的机械模型如下。关于DH建模的更多细节可以参考我的另一篇博文->【机器人学】机器人运动学基础。

除此之外，为了计算的简便，越来越多的人开始使用PoE进行建模，关于PoE建模的方法可以参考我的这篇文章->【机器人学】基于PoE模型的串联机械臂UR5的正运动学、微分运动学和逆运动学，其中基于PoE模型对UR5进行了运动学分析。

说到DH参数就涉及到了机器人DH参数标定的问题。

机器人运动学参数标定（DH参数标定）

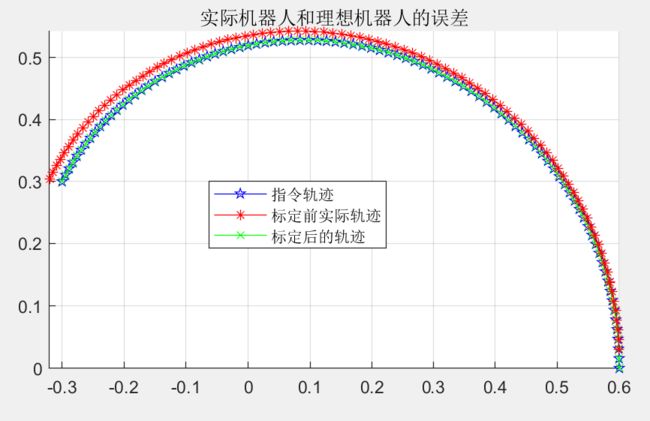
同时给出辨识后的结果：

可以清晰的看出，辨识后的机器人精度更高了。高自由度的机械臂，例如，六自由度且相邻转轴出现平行的情况，可以参考我的另一篇博文->【【机器人算法】机器人运动学参数辨识/DH参数校准/DH参数辨识

运动学逆解

由于是2自由度，因此只考虑位置。

解析解

一般都是用几何法求解。其中需要注意的是构型的选择，elbow up和elbow down两种，同时需要注意三角函数对解的范围的限制。高自由度的机械臂，例如，七自由度的可以参考我的另一篇博文->【机器人学】冗余七自由度机械臂的解析解逆解算法

数值解

一般都是用雅可比矩阵（广义逆）进行迭代。这里也不举例了。
具体算法可以参见我的另一篇博文->【机器人学】机械臂数值解逆解

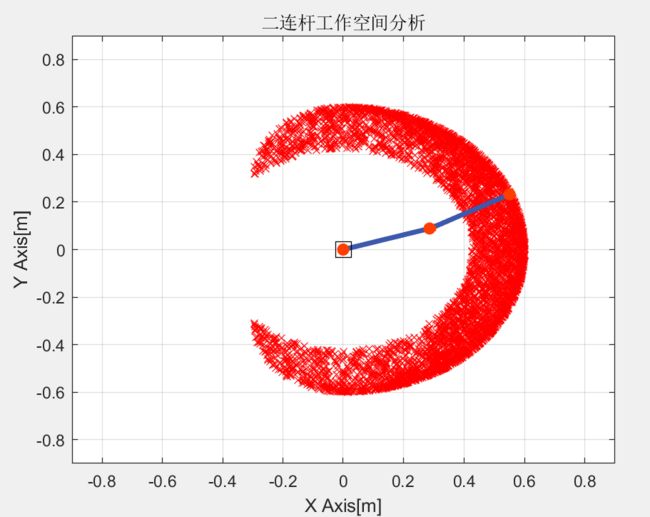
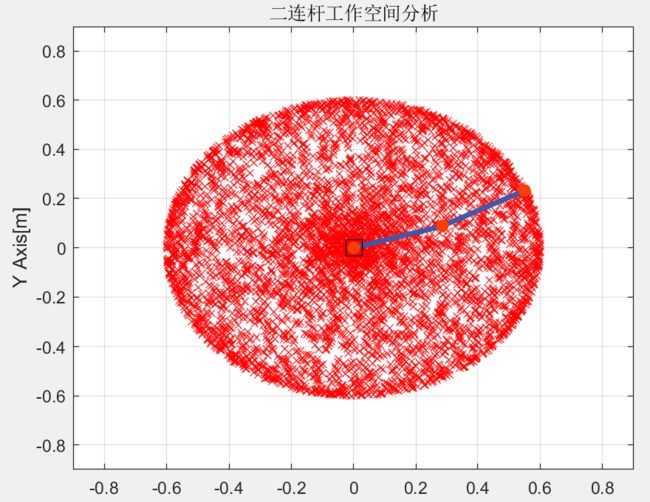
工作空间分析

这里设关节限位为(-pi/2,pi/2)

关节限位为(-pi,pi)的情况：

可操纵性

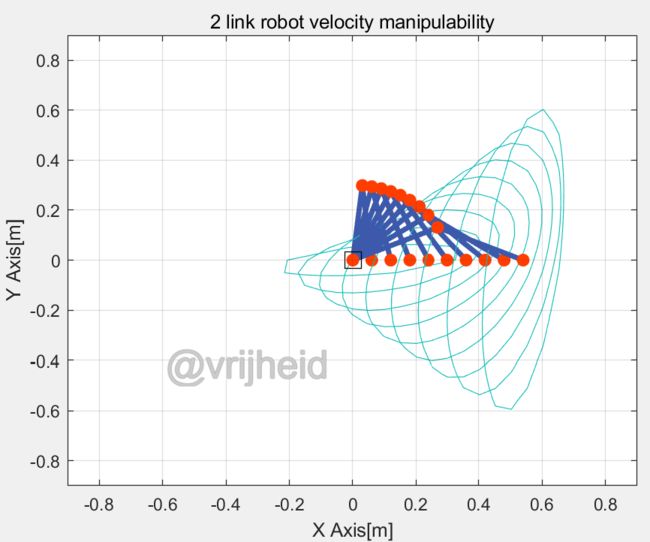
可操纵性度量：

轨迹规划

这里给出一种在笛卡尔空间的轨迹规划，用的是数值解来迭代。

路径规划

这里直接给出一种，RRT算法在关节空间的路径规划（效率更高），其中包括了碰撞检测。其中关于RRT算法可以参考我的另一篇博文->【路径规划】RRT(Rapidly-exploring Random Trees)算法、关于碰撞检测算法可以参考我的另一篇博文->【算法】基于包围盒的机器人碰撞检测
RRT算法的展示如下：

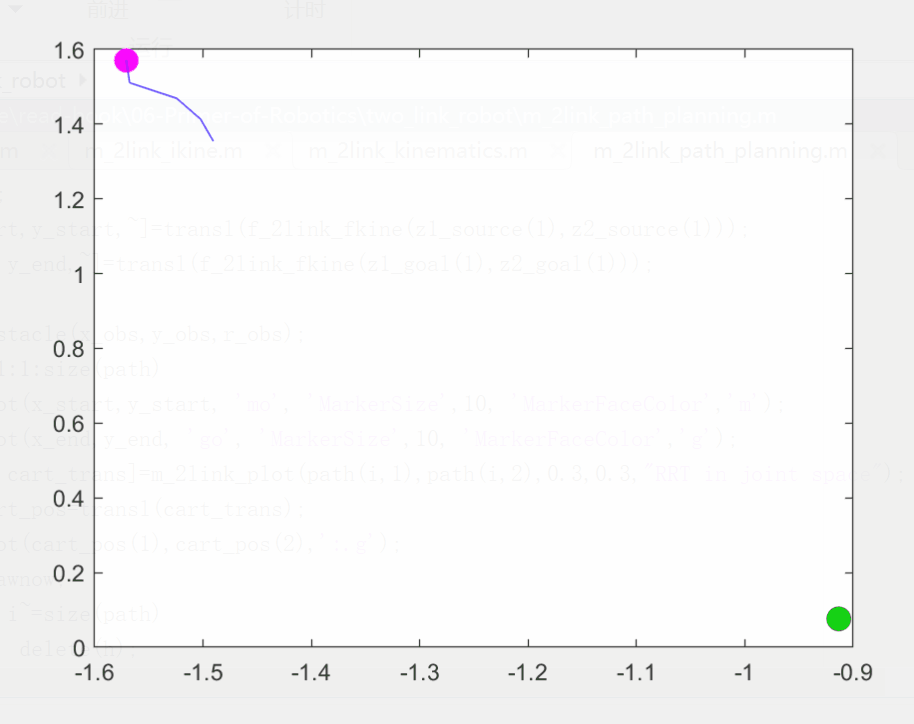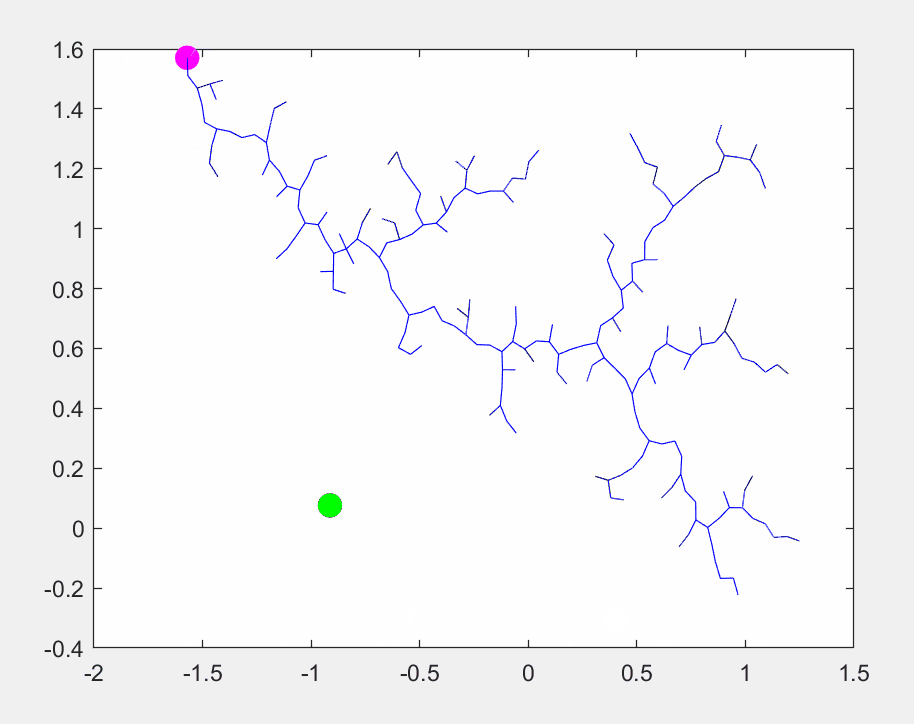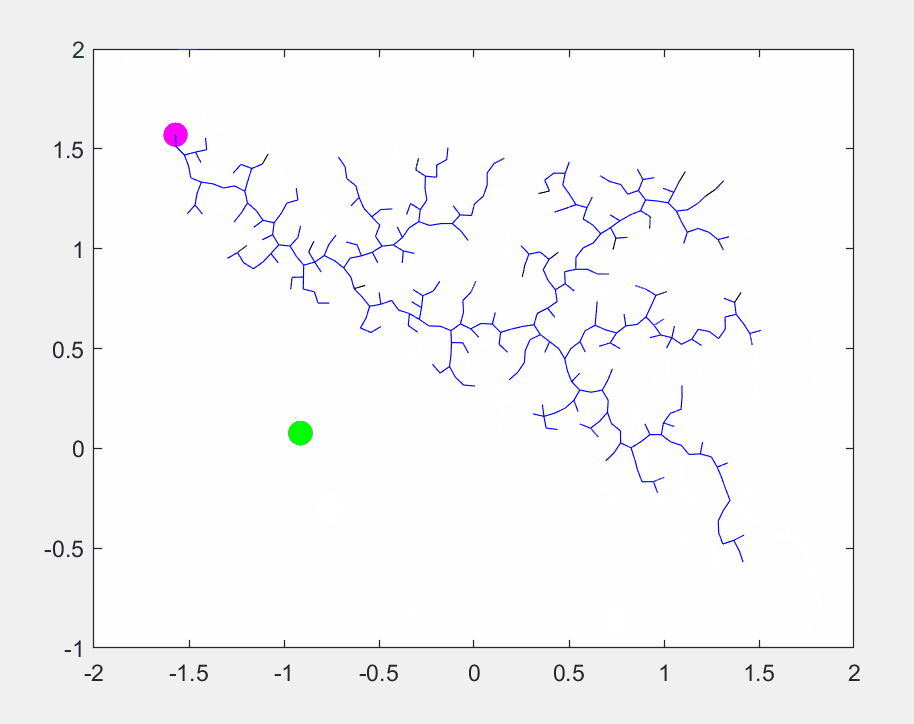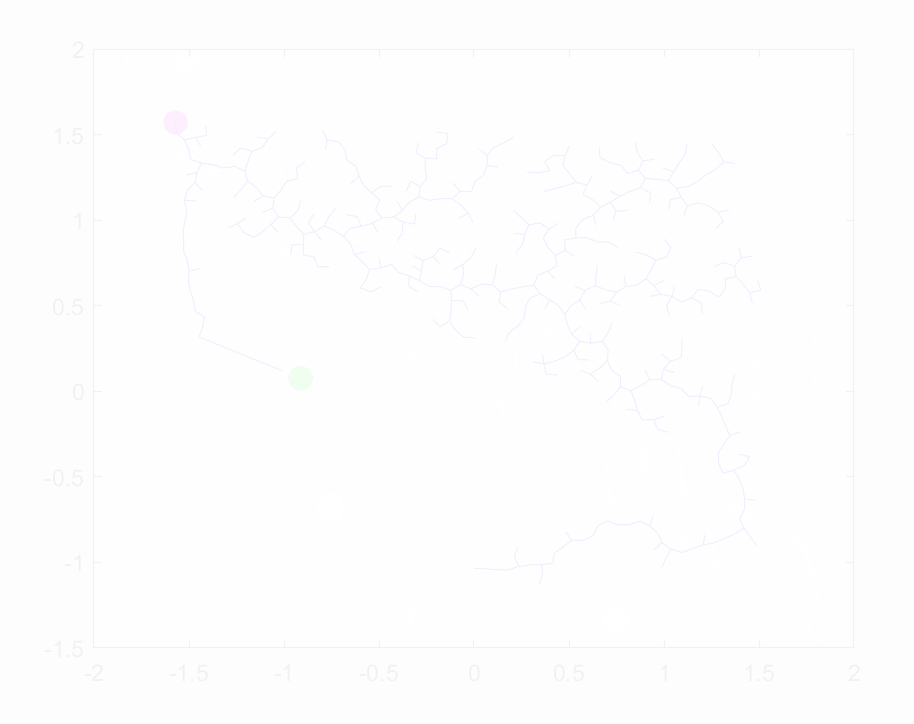
实际运行效果如下：

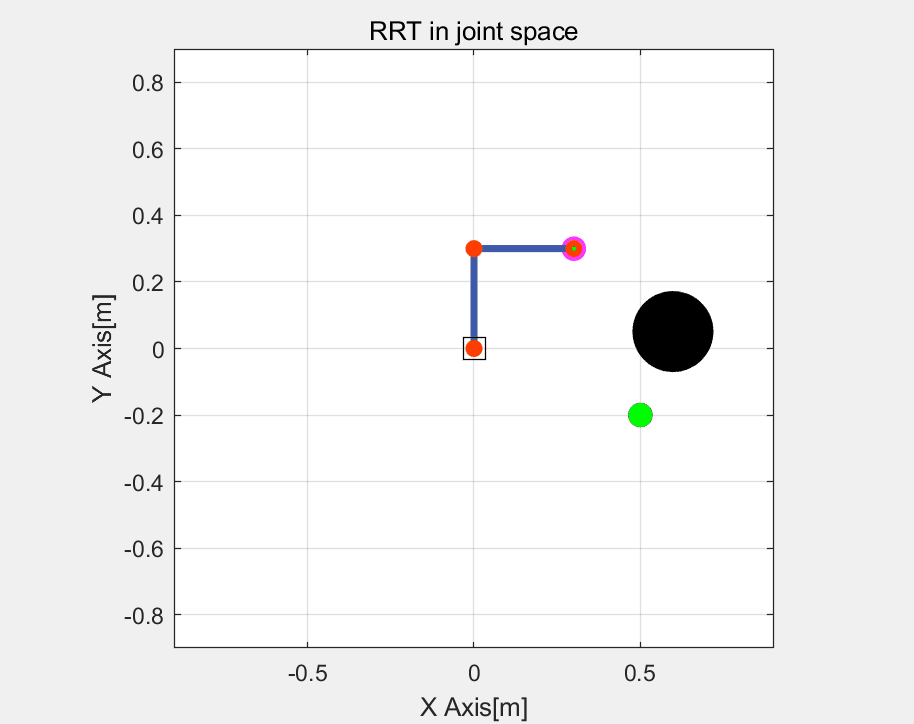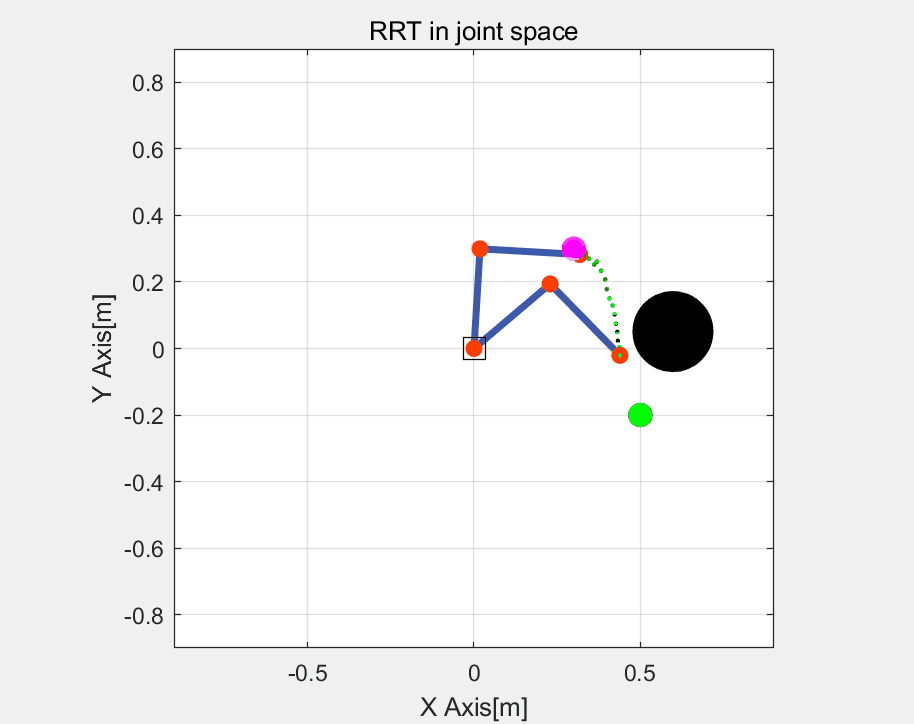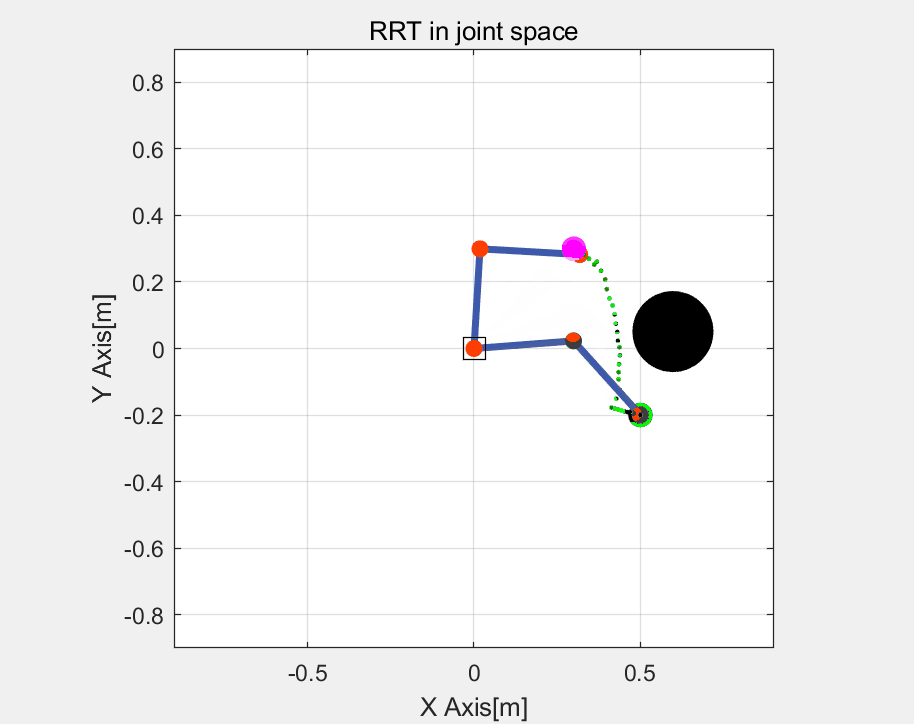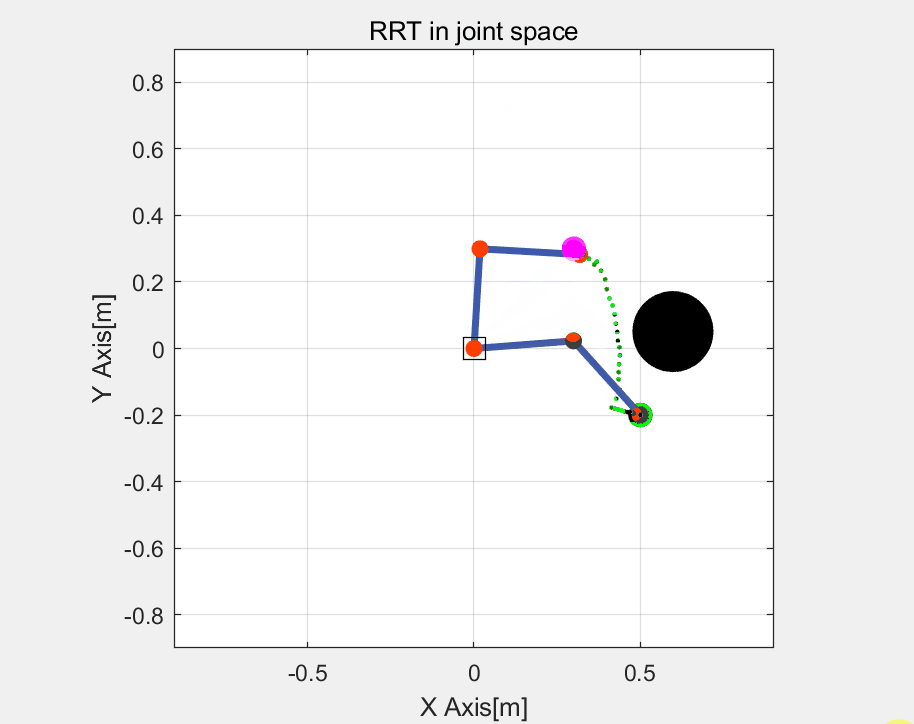
关节轨迹：

静力学

静力学其实就是“虚功原理”，更多的体现在动力学中，这里没什么可展示的。

动力学

首先是动力学模型的建立，建立动力学方程推荐使用牛顿欧拉法，计算量更小，更方便计算机迭代运算。

动力学模型

拉格朗日法和牛顿欧拉法的结果是相同的，动力学方程如下：

但是在常见的控制及参数辨识过程中，方程通常写为如下形式：

这里我们暂且不考虑摩擦力。

C虽然是可以随便选择的，但是应当符合动力学模型的典型性质。
求得的离心力和科氏力相关的C及动力学模型的典型性质如下：

这个性质称之为动力学模型的反对称性。

得到动力学方程后，我们就可以利用动力学方程进行控制和优化了。

动力学仿真

根据机器人的动力学方程可以做动力学仿真如下：
这里主要给出2连杆在只受重力的作用下自由下落、遇到“跳床”和重力配平。

自由下落

可以看出在重力的作用下2连杆的自由下落过程。

遇到跳床

可以看出在重力的作用下2连杆的自由下落时遇到弹簧的运动过程。

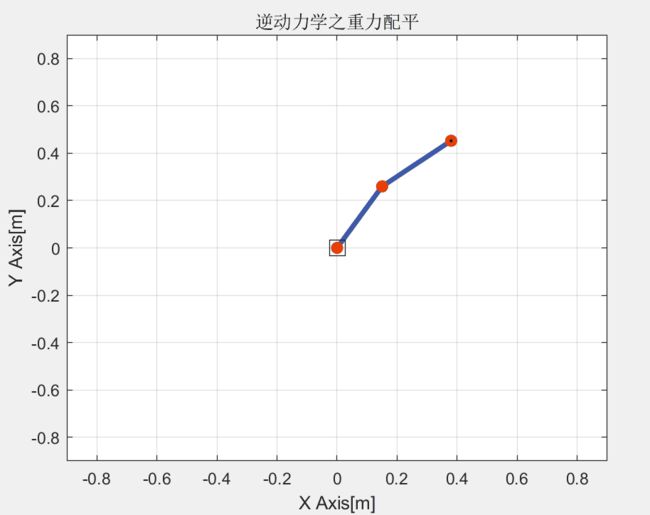
重力补偿

可以看出在有重力的作用下，进行了重力配平，2连杆并没有落下。

说到动力学其中的一个难点就是动力学参数辨识。

动力学参数辨识

动力学参数辨识是一个比较复杂的难点，这里另开一章进行讲解->【机器人算法】机器人动力学参数辨识

控制

这里的控制都是基于机器人动力学。

位置控制

这里的位置控制是PD控制。

对比实际轨迹和期望轨迹可以看出，实际轨迹出现交大偏差，简单来说这主要是由于PD参数调的不好(这里的PD参数是根据经验调出的)。

至于“调PID的东西”，属于机械臂的运动控制的范畴，大致可以分为：

• 多关节分散控制：不考虑连杆的动力学（只考虑重力），然后调节PID参数。这里可以参考->【运动控制】机械臂的分散控制（Decentralized Control）
• 多关节集中控制：考虑连杆动力学，基于状态方程“调节PID”。-> 【运动控制】机械臂的集中控制(Centralized Control)

其中电机建模的基础可以参见：-> 【运动控制】直流电机的建模与位置控制和力控制

力控制

机器人里力控主要可以归类为三个：

• 力控制：给出目标力去跟踪；
• 力位混合控制：力和位置相互正交，相互独立，控制律简单。
• 阻抗控制：属于一种“没有目标”的控制，适用于人机交互。

力位置混合控制

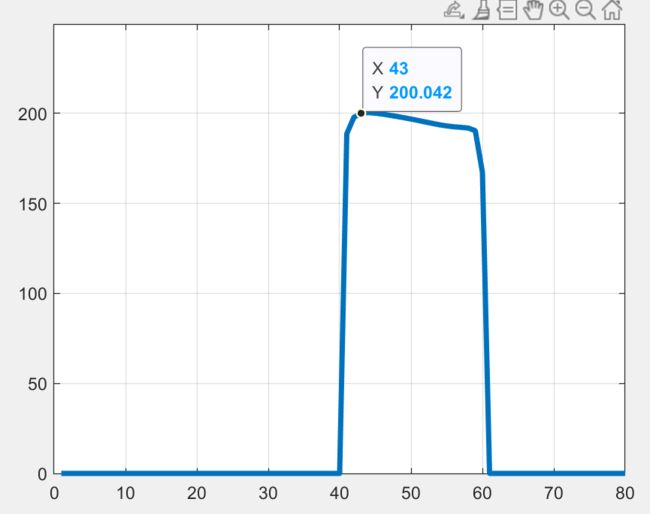
根据仿真结果可以看出，机械臂末端在接触墙壁时，同时进行了力的控制（约200N）

控制力为：

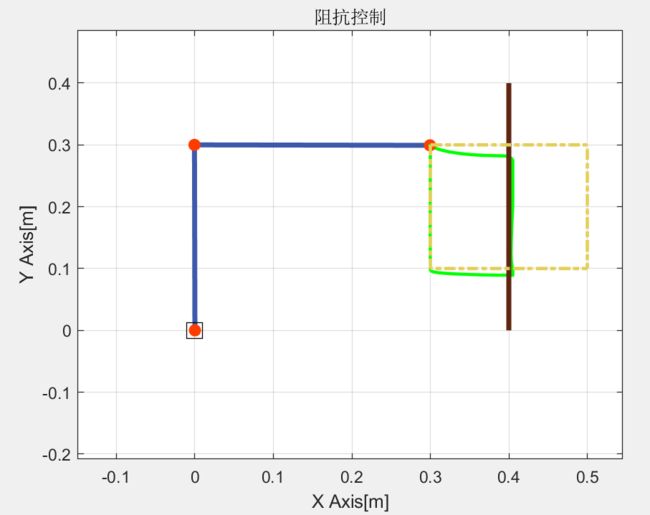
阻抗控制

首先看结果，其中黄色虚线为指令轨迹，可以看出机械臂在撞击墙壁时，机械臂并没有出现不稳定的现象，这是由于阻抗控制的关系。
可以看出实际轨迹和指令轨迹误差较大，这是由于：

• 阻抗刚度系数太小，但是太多在发生撞击时会不稳定。
• 没有重力配平

再看整个运动过程：