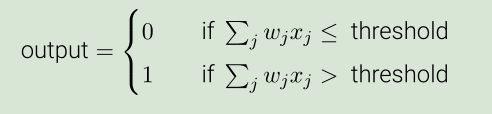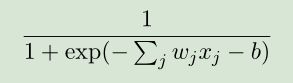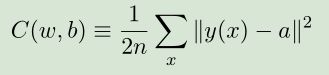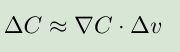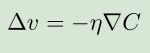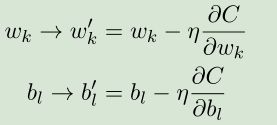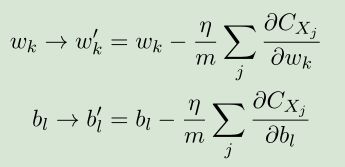神经网络与深度学习笔记——梯度下降算法是什么？

神经网络与深度学习笔记系列一共有五个专题，分别是

第一章使用神经网络识别手写数字——梯度下降算法是什么。主要介绍了神经网络的基础例如感知器激活函数等概念，最主要介绍了梯度下降算法。

第二章反向传播算法如何工作——反向传播算法原理。主要介绍了反向传播算法的工作原理。

第三章改变神经网络的学习方法——代价函数，规范化，过拟合。主要介绍了不同的代价函数，以及规范化等对传统代价函数的改造。

第四章深度神经网络为何难以训练——梯度消失和爆炸。主要介绍了梯度消失问题和梯度爆炸问题。

第一章 使用神经网络识别手写数字

1.1感知器

                                                                    

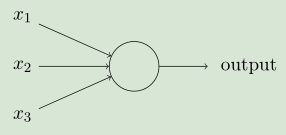
多输入（二进制输入，0或者1），单输出（0或1）的人工神经元。通俗地讲就是每一个输入xi都对应着一个权重wi，同时感知器自身具有偏置b（阈值），感知器所做的事情是对所有的输入xi和其对应的权重wi相乘并求和，最终加上偏置b，所得的值与0作比较，输出0或者1。

                                                        

                                                                  

1.2S型神经元

                                                                    

多输入（0和1之间的任意值，例如0.61821455....），单输出（0和1之间的任意值）的人工神经元。通俗地讲就是，对于每一个输入xi，S型神经元都有一个与之对应的权重wi，并且S型神经元具有sigmoid激活函数，偏置项b，S型神经元做的计算为：

                                                                  

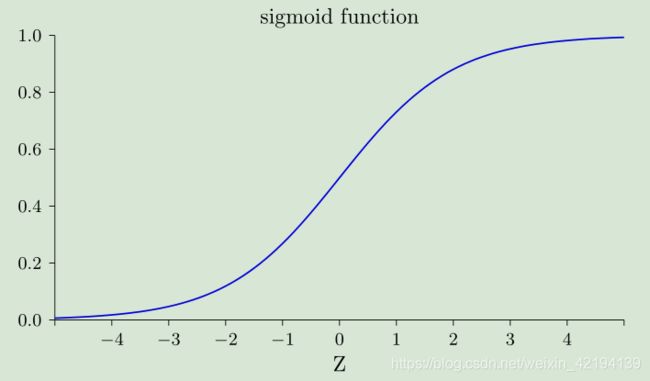
sigmoid函数公式和函数图像为：

                                                                        

                     

这样就能达到学习算法的目的（微小改变w和b，输出同样做出微小改变）。这就是感知器所不具备的特点，对于感知器而言，微小改变△w和△b，很可能使输出由0变为1或者由1变为0，达不到学习算法的目的，即通过调整△w和△b来微小调整输出△output。而S型神经元因为使用了非线性激活函数，具有平滑性，可以计算：

                                     

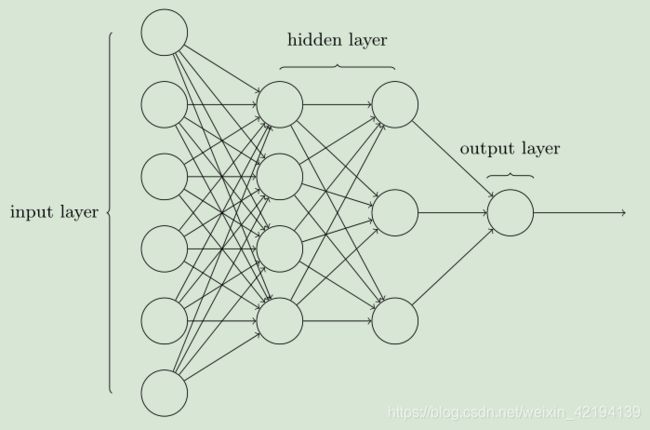
1.3神经网络的构架

                    

上图为的网络被称为多层感知器（MLP），此感知器并不是1.1节中所提到的感知器，为了避免混淆，本书会刻意不使用MLP这个术语。

输入层，输入神经元。输出层，输出神经元。隐藏层，隐藏神经元。

前馈神经网络：上一层的输出作为下一层的输入。网络中没有环路，信息总是向前传播不方向传播。

1.4本书采用的识别手写数字的神经网络结构

                                   

1.5梯度下降算法进行学习

将每个训练输入x看作是一个28*28=784维的向量，期望输出为一个10维的向量，采用one-hot形式表示。

学习算法的目的是找到合适的权重w和偏置b使得神经网络识别效果最好，识别效果最好怎样显式地表现出来呢？我们定义了一个代价函数（目标函数，损失函数），利用梯度下降算法使得代价函数达到最小值，我们就认为神经网络的识别效果达到最好，这样问题就转变成了求函数最小值的问题。

我们采用的代价函数是二次代价函数（均方误差，MSE）。

                                                    

n表示训练数据的个数，y（x）表示期望输出，a表示神经网络的预测输出，对所有的训练输入数据x求和。||v||表示向量v的模。

现在有了要最小化的函数，那么我们采用什么样的方才来最小化这个二次代价函数呢？这里我们采用的是梯度下降法。

假设C是一个具有m个变量v1，v2，v3.......vm的函数，C中自变量的变化量△v=（△v1，△v2.....△vm）^T，C的梯度向量为：

                                                                            

C的变化量△C可以表示为：

                                                                                   

我们使得C最小，就要使△C<0，我们怎样取△v的值才能使得△C<0呢？

我们取：

                                                                                     

其中η是一个很小的正数，称为学习速率。我们可以通过这样的△v来不断更新v，使C减小，最终理想情况下达到最小值。更新v的公式为：

这个更新v的公式就是梯度下降算法的核心思想，也可以称其为梯度下降算法公式。

让我们回到代价函数是如何利用梯度下降算法来更新权重w和偏置b以实现达到代价函数的最小值的目标的。神经网络中代价函数C是权重w和偏置b的函数，利用梯度下降算法来更新w和b的公式是：

                                                                

以上就是梯度下降算法以及在神经网络中代价函数C如何利用梯度下降算法来更新权重w和偏置b以达到最小值的介绍，下面让我们再来观察代价函数的公式。

可以看到，代价函数C是将训练集中所有的训练数据（向量）xi所产生的代价函数值相加，这样在训练集很大时就会产生很复杂的计算，需要花费很多时间，使学习变得很缓慢。一个解决办法就是采用随机梯度下降算法作为神经网络的学习算法。

随机梯度下降算法就是每次训练并不是把训练集中所有的数据都输入到神经网络中进行训练，计算代价函数，而是在每次训练时，随机选取训练集中小量的数据例如m（x1，x2，x3.....xm）个数据进行训练，用它们训练产生的代价函数所求出的梯度作为整个训练集的梯度的平均值，进行权重和偏置的更新。即：

                                                           

                                                                    

更新权重w和偏置b：

                                                            

在训练集中随机选取的这一组训练数据（x1，x2，.....xm）称为一个小批量数据（mini-batch），在只一组mini-batch完成训练以后，然后我们再从训练集中挑选另一组mini-batch，直到我们用完训练集中的所有数据，这被称为完成了一个训练迭代期（epoch）。然后我们开始一个新的epoch。

一个极端的版本是mini-batch为1，也就是每次只训练一个数据，然后更新我们的权重和偏置。然后再输入一个数据进行权重和偏置的更新。这个过程被称为在线、online。on-line或者递增学习。