前方交会与后方交会
1.前方交会
1.1 前方交会的概念
利用立体像对两张像片的内方位元素、同名像点坐标和像对的相对方位元素(或外方位元素)解算模型点坐标(或地面点坐标)的工作,称为空间前方交会。在摄影测量中主要有两种:
1.利用立体像对两张像片的相对方位元素,计算模型点的三位坐标;
2.利用立体像对两张像片的外方位元素,计算地面点的地面坐标。

1.2 前方交会基本关系式
 要确定像点与其对应的模型点(地面点)的数学表达式,如上图所示,D-XYZ为地面摄影测量坐标系,S~1~ - U~1~V~1~W~1~及S~2~ - U~2~V~2~W~2~分别为左右像片的像空间辅助坐标系,且两个像空间辅助坐标系的三个轴分别与D-XYZ三轴平行。
要确定像点与其对应的模型点(地面点)的数学表达式,如上图所示,D-XYZ为地面摄影测量坐标系,S~1~ - U~1~V~1~W~1~及S~2~ - U~2~V~2~W~2~分别为左右像片的像空间辅助坐标系,且两个像空间辅助坐标系的三个轴分别与D-XYZ三轴平行。
设地面点A在D-XYZ坐标系中的坐标为(X,Y,Z),地面点A在S1 - U1V1W1及S2 - U2V2W2的坐标分别为(U1,V1,W1)及(U2,V2,W2),A点相应的像点坐标a1、a2的像空间坐标为(x1,y1,-f)、(x2,y2,-f),像点的像空间辅助坐标为(u1,v1,w1)、(u2、v2、w2),则有:

式中的R1,R2为已知的外方位元素计算的左右像片的旋转矩阵。右摄影站点S2在S1 - U1V1W1中的坐标,即摄影基线B的三个分量Bu,Bv,Bw,可由外方位线元素计算:

因左、右像空间辅助坐标系及D-XYZ相互平行,且摄影站点、像点、地面点三点共线,由此可得出:
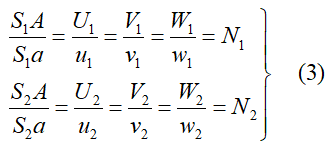
式中的N1、N2分别称为左、右像点的投影系数。U1、V1、W1为地面点A在S1 - U1V1W1中的坐标,U2、V2、W2为地面点A在S2 - U2V2W2中的坐标,且
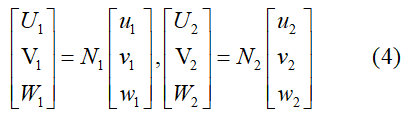
最后得出地面点坐标的公式为:

一般地,在计算地面点Y坐标时,应取均值,即
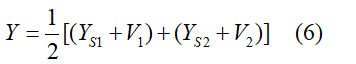
考虑到(2)式,(5)式又可变为:
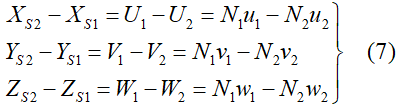
由上式的一、三式联立求解,得投影系数的计算式为:
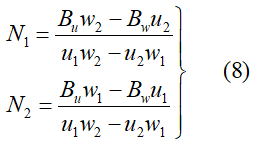
1.3 前方交会代码
//利用像片外方位元素进行前方交会
#include2.后方交会
2.1 后方交会的概念
空间后方交会的定义是利用地面控制点及其在像片上的像点,确定单幅影像外方位元素的方法。如果已知每张像片的6个外方位元素,就能确定被摄物体与航摄像片的关系,因此,如何获取像片的外方位元素,一直是摄影测量工作者所探讨的问题。目前,采用的测定方法有:利用雷达、全球定位系统(GPS)、惯性导航系统(WS)以及星相摄影机来获取像片的外方位元素;也可利用摄影测量空间后方交会,如下图所示,该方法的基本思想是利用至少三个已知地面控制点的坐标A(XA,YA,ZA)、B(XB,YB,ZB),C(XC,YC,ZC),与其影像上对应的三个像点坐标a(xa,ya)、b(xb,yb)、c(xc,yc),根据共线方程,反求该像片的外方位元素XS、YS、ZS、 ϕ \phi ϕ、 ω \omega ω、 κ \kappa κ。这种解算方法是以单张像片为基础,亦称单像空间后方交会。

2.2 后方交会基本关系式
空间后方交会采用的基本关系式为下面的共线条件方程式:

由于共线条件方程是非线性函数模型,为了便于计算,需把非线性函数表达式用泰勒公式展开为线性形式,人们常把这一数学处理过程称为“线性化”。
将共线式线性化并取一次小值项得:
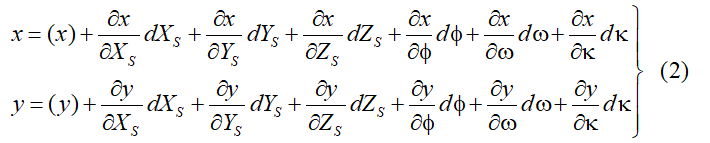
式中,(x)、(y)为函数的近似值,是将外方位元素初始值XS0、YS0、ZS0、 ϕ \phi ϕ0、 ω \omega ω0、 κ \kappa κ0带入共线条件式所取得的数值。dXS、dYS、dZS、d ϕ \phi ϕ、d ω \omega ω、d κ \kappa κ为外方位元素近似值的改正数。那些偏导数是外方位元素改正数的系数。对于每一个控制点,把像点坐标x、y和相应地面点摄影测量坐标X、Y、Z代入(2)式,就能列出两个方程式。若像片内有三个已知地面控制点,就能列出六个方程式,求出六个外方位元素的改正值。由于(2)式中系数仅取泰勒级数展开式的一次项,未知数的近似值改正是粗略的,所以计算必须采用逐渐趋近法,解求过程需要反复趋近,直至改正数小于某一限值为止。
2.3 后方交会的误差方程式与法方程式
2.4 后方交会流程
①获取已知数据:
从摄影资料中查取像片比例尺1/m,平均航高,内方位元素x0,y0,f;
从外业测量成果中,获取控制点的地面测量点坐标Xt,Yt,Zt,并转化为地面摄影测量坐标X、Y、Z。
②量测控制点的像点坐标:
将控制点标刺在像片上,利用立体坐标量测仪量测控制点的像框标坐标,并经像点坐标改正,得到像点坐标x、y。
③确定参数初值:
参数的初值即XS0,YS0,ZS0, ϕ \phi ϕ0, ω \omega ω0, κ \kappa κ0。在竖直航空摄影且地面控制点大体对称分布的情况下,可按如下方法确定初值:

④计算旋转矩阵:
利用角元素的近似值计算方向余弦值,组成R矩阵。
⑤计算像点坐标近似值:
利用参数的近似值,按共线方程计算各个控制点对应像点的像平面坐标近似值xi0,yi0(i=1,2,…n)。
⑥组成误差方程式:
一个控制点对应的误差方程为
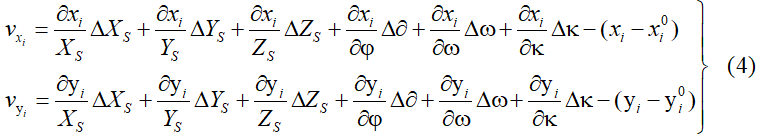
写成矩阵形式为 Vi = Ai X – Li ,其中系数矩阵A中的元素均为偏导数。

为了计算这些偏导数,引入以下记号:
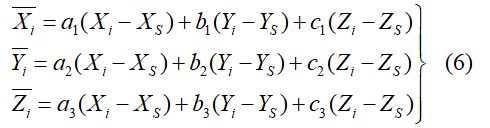
推导过程就是各种求偏导数,这里不再描述,直接给出A矩阵中的系数结果

对每一个控制点,计算其对应的方程的系数矩阵Ai、常数项Li,然后联立起来,得:

记为
![]()
⑦组成法方程式:计算法方程式的系数矩阵和常数项
按最小二乘原理,取权阵为单位阵,则法方程为:
![]()
这一步骤需要计算出ATA和ATL。
⑧解求外方位元素:
根据法方程,按下式解求外方位元素改正数,并与相应的近似值求和,得到外方位元素新的近似值。
![]()
⑨检查计算是否收敛:
将求得的外方位元素的改正数与规定的限差比较,小于限差则计算终止,否则用新的近似值重复进行第④至第⑧步的计算,直到满足要求为止。
2.5 后方交会评价精度
按照上述方法求得的外方位元素,其精度可以通过法方程的系数矩阵的逆矩阵来求得,即
![]()
协因数阵Q的对角线Qii就是第i个未知数的权倒数。若单位权中误差为m0,则第i个微指数的中误差为:
![]()
当参加空间后方交会的控制点有n个时,单位权中误差可按下式计算:
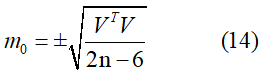
2.6 后方交会代码
#include