数据分析｜透彻地聊聊k-means聚类的原理和应用

K-Means 是一种非监督学习，解决的是聚类问题。K 代表的是 K 类，Means 代表的是中心，你可以理解这个算法的本质是确定 K 类的中心点。当你找到了中心点，也就完成了聚类！

可以从以下三个角度来梳理k-means：

如何确定 K 类的中心点？
如何将其他点划分到k类中？
如何区分k-means与k-近邻算法？

为了对k-means有个感性的认识，我们从熟悉的场景亚洲足球队的水平开始谈起：

熟悉足球的朋友可能心理已经有了预期？你可能会说，”伊朗，韩国“一流水平，中国”二流水平“，越南”三流水平“。这样的猜测是基于我们的经验。

那么，伊朗，中国，越南就是三个等级的代表---中心。

那么如何确定k类的中心了？一开始我们是随机指认的，当确定了中心点后，我们就可以按照距离将其它足球队划分到不同的类别中。

在这里我们默认k=3，在工业界k的选择是个难事！但我们可以通过其它方式来确定k，后文会讲到。

从上面的描述中，我们可以抽象出聚类方法的步骤：

1. 随机从数据集中选择k个点作为我们聚类的中心点；
2. 讲每个点分配到离它最近的类中心点，就形成了k类。然后重新计算每个类的中心点（比如取各类的均值作为新的中心点）
3. 重复第2步，直到类不再发生变化，或者设置最大迭代次数，让算法收敛。

下面举例说明，上述过程：

其中 2019 年国际足联的世界排名，2015 年亚洲杯排名均为实际排名，2018年，很多球队没有入围决赛，进入决赛圈的有自己的排名，没有进入决赛圈我们按照以下原则来给其一个排名：

如果是亚洲区域入选赛12强的队伍，设置为40名
如果没有进入亚洲区域预选赛，设置为50名

数据太过于分散，量级相差过大，通过特征工程中的最大最小归一化来对数据进行处理（也可以是z-评分归一化），得到如下的数据：

#最大最小归一化处理
# coding:utf-8
from sklearn import preprocessing
import numpy as np
# 初始化数据，每一行表示一个样本，每一列表示一个特征
x = np.array([[ 0., -3.,  1.],
              [ 3.,  1.,  2.],
              [ 0.,  1., -1.]])
# 将数据进行 [0,1] 规范化
min_max_scaler = preprocessing.MinMaxScaler()
minmax_x = min_max_scaler.fit_transform(x)
print minmax_x

#z-评分归一化处理
from sklearn import preprocessing
import numpy as np
# 初始化数据
x = np.array([[ 0., -3.,  1.],
              [ 3.,  1.,  2.],
              [ 0.,  1., -1.]])
# 将数据进行 Z-Score 规范化
scaled_x = preprocessing.scale(x)

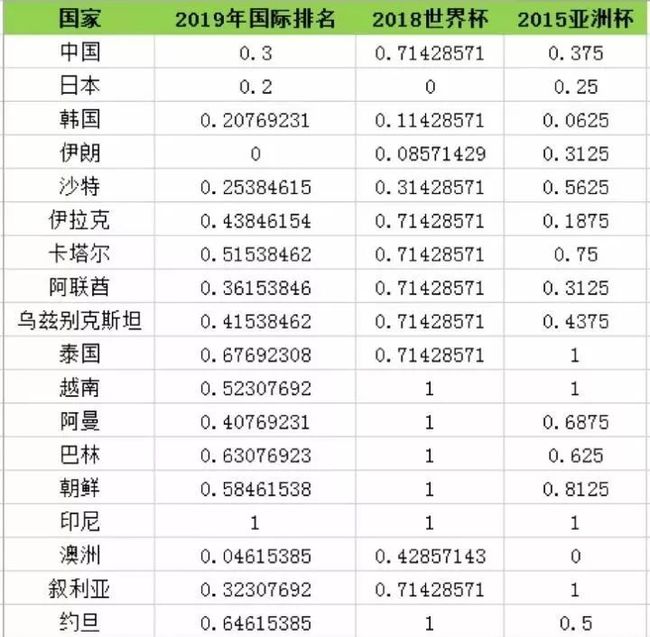
接下来，开始计算各个足球队举例k类中心点的距离，距离的距离方式有很多，这里我们选择欧式距离。

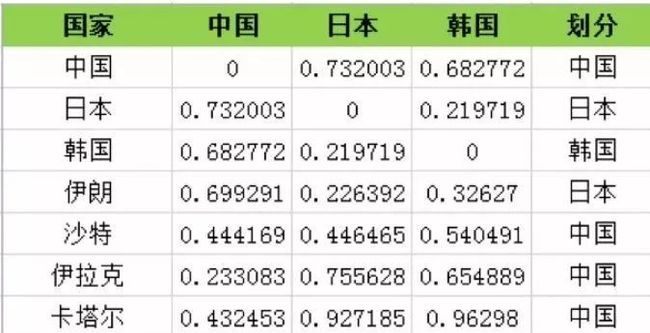
那么你是如何计算中国与日本的距离？
采用欧式距离，默认19年，18年，15年的数据权重是一样的，比如中国与日本的距离：

根据初始随机选择的k类中心点：中国，韩国，日本，我们计算各俱乐部与三类中心点的距离，各俱乐部就近选择中心点（就有了划分这一列）。划分这一列是我们迭代一次后的聚类结果，显然不是最优。

那么如何更新中心点了？

选择同一类别下各个俱乐部三个指标下各自的平均值作为新的聚类中心（聚类中心是三个特征值哦）。

为什么会使用均值作为中心点的选择呢？这主要是由于我们目标函数的设置有关。我们使用误差平方和作为聚类的目标函数，就要求我们最终选择均值为聚类中心点迭代的原则。

这样不端迭代，直到达到迭代次数或是类别不再发生变化，结束。

最终的聚类结果，如下图：

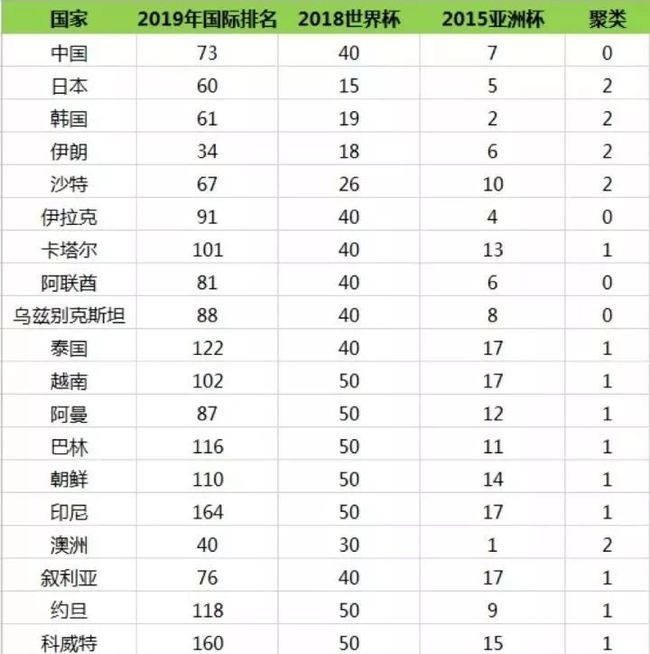
如何使用 sklearn 中的 K-Means 算法

# coding: utf-8
from sklearn.cluster import KMeans
from sklearn import preprocessing
import pandas as pd
import numpy as np
# 输入数据
#np.random.seed(1234) #不加随机数种子，每次聚类结果都不一样
data = pd.read_csv('data.csv', encoding='gbk')
train_x = data[["2019 年国际排名 ","2018 世界杯 ","2015 亚洲杯 "]]
df = pd.DataFrame(train_x)
kmeans = KMeans(n_clusters=3)
# 规范化到 [0,1] 空间
min_max_scaler=preprocessing.MinMaxScaler()
train_x=min_max_scaler.fit_transform(train_x)
# kmeans 算法
kmeans.fit(train_x)
predict_y = kmeans.predict(train_x)
# 合并聚类结果，插入到原数据中
result = pd.concat((data,pd.DataFrame(predict_y)),axis=1)
result.rename({0:u'聚类'},axis=1,inplace=True)
print(result)


国家  2019年国际排名  2018世界杯  2015亚洲杯  聚类
0     中国       73     40       7   2
1     日本       60     15       5   0
2     韩国       61     19       2   0
3     伊朗       34     18       6   0
4     沙特       67     26       10   0
5    伊拉克      91     40       4   2
6    卡塔尔      101    40       13   1
7    阿联酋      81     40       6   2
8  乌兹别克斯坦   88     40       8   2
9     泰国      122     40       17   1
10    越南      102     50       17   1
11    阿曼      87      50       12   1
12    巴林      116     50       11   1
13    朝鲜      110     50       14   1
14    印尼      164     50       17   1
15    澳洲      40      30       1   0
16   叙利亚     76      40       17   1
17    约旦      118     50       9   1
18   科威特     160      50      15   1
19  巴勒斯坦     96      50      16   1

因为初始中心点是随机选择的，所以每次的聚类结果都不一样，这就要求我们加上随机数种子！加入随机数种子只是保证我们的结果稳定不变，并不代表当前的聚类结果就是最好的。也就是说，聚类结果依赖于初始中心点的选择！

参数设置：

当然 K-Means 只是 sklearn.cluster 一共提供了 9 种聚类方法，比如 Mean-shift，DBSCAN，Spectral clustering（谱聚类）等

KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')

总结：

如何区分k-means与knn：

k-means是聚类算法，knn是有监督的分类算法；聚类没有标签，分类有标签

聚类算法中的k是k类，knn中的k是k个最近的邻居。

k-means优点：

计算简单，可解释性强。

k-means缺点：

需要确定分类数，一般根据经验或者已经有预判，其次是根据R语言提供的暴力试错k值选择最合适的分类数k。

初始值的选取会影响最终聚类效果，并且目标函数可能会达到局部最优解。这个有相应的改进方法，包括k-means++和二分k-means。

算法本身的局限性：对于类似下面圆形的数据集，聚类效果很差，主要是算法原因。所以还有其他的聚类算法，比如基于密度的方法等。

不适合发现非凸形状的簇或者大小差别较大的簇；

对噪声和异常点比较敏感

End.

作者：求知鸟

来源：知乎