积分图(三) - Boxfilter 的实现过程分析
Boxfilter 快速计算
它可以使复杂度为O(MN)的求和,求方差等运算降低到O(1)或近似于O(1)的复杂度,它的缺点是不支持多尺度。
Boxfilter 的原理有点类似 Integral Image,而且比它还要快,但是实现步骤比较复杂。在计算矩形特征之前,Boxfilter 与 Integral Image 都需要对图像进行初始化(即对数组A赋值), 不同于 Integral Image, Boxfilter 的数组 A 中的每个元素的值是该像素邻域内的像素和(或像素平方和), 在需要求某个矩形内像素和的时候,直接访问数组中对应的位置就可以了。因此可以看出它的复杂度是O(1)。
Boxfilter 的初始化过程如下:
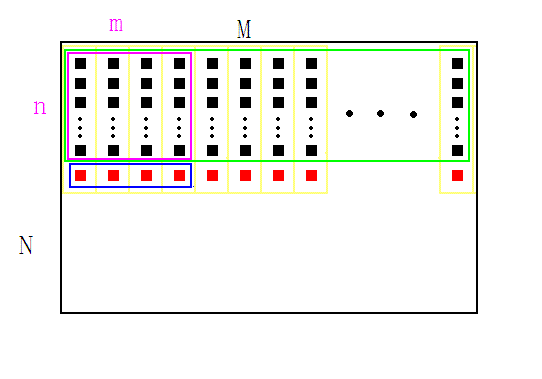
1、给定一张图像,宽高为(M,N),确定待求矩形模板的宽高(m,n),如图紫色矩形。图中每个黑色方块代表一个像素,红色方块是假想像素。
2、开辟一段大小为 M 的数组,记为 buff, 用来存储计算过程的中间变量,用红色方块表示.
3、将矩形模板(紫色)从左上角(0,0)开始,逐像素向右滑动,到达行末时,矩形移动到下一行的开头(0,1),如此反复,每移动到一个新位置时,计算矩形内的像素和,保存在数组 A ( buff 只是用来缓存中间变量的)中。以 (0,0) 位置为例进行说明:首先将绿色矩形内的每一列像素求和,结果放在 buff 内(红色方块),再对蓝色矩形内的像素求和,结果即为紫色特征矩形内的像素和,把它存放到数组A中,如此便完成了第一次求和运算。
4、每次紫色矩形向右移动时,实际上就是求对应的蓝色矩形的像素和,此时只要把上一次的求和结果减去蓝色矩形内的第一个红色块,再加上它右面的一个红色块,就是当前位置的和了,用公式表示 sum[i] = sum[i-1] - buff[j] + buff[j+m].
5、当紫色矩形移动到行末时,需要对 buff 进行更新。因为整个绿色矩形下移了一个像素,所以对于每个buff[i], 需要加上一个新进来的像素,再减去一个出去的像素,然后便开始新的一行的计算了。
Boxfilter 的初始化过程非常快速,每个矩形的计算基本上只需要一加一减两次运算。从初始化的计算速度上来说,Boxfilter 比 Integral Image 要快一些,大约 25%。在具体求某个矩形特征时,Boxfilter 比 Integral Image 快 4 倍,所谓的 4 倍其实就是从 4 次加减运算降低到 1 次,虽然这个优化非常渺小,但是把它放到几层大循环里面,还是能节省一些时间的。对于那些实时跟踪检测算法,一帧的处理时间要严格在 40ms 以下,正是这些细小的优化决定了程序的效率,积少成多,聚沙成塔。
下面的程序是Boxfilter的示例代码,谨供参考
.hpp
#pragma once
typedef unsigned char uchar;
class Boxfilter
{
public:
Boxfilter(void);
~Boxfilter(void);
void init(int width, int height, int mwidth=5, int mheight=5);
void boxfilter(unsigned char* img);
public:
float getMean(int x, int y); //以x,y为中心点,mwidth,mheight为直径的局部区域,下同
float getVar(int x, int y);
int getSum(int x, int y);
int getSquareSum(int x, int y);
int getLocalSize();
private:
int mwidth ;
int mheight ;
unsigned char* img;
int width;
int height;
int* f_sum;
int* f_sum2;
};.cpp
#include "Boxfilter.h"
#include
#include
int* buff = 0;
int* buff2 = 0;
int boxwidth;
int boxheight;
Boxfilter::Boxfilter(void)
{
f_sum = 0;
f_sum2 = 0;
}
Boxfilter::~Boxfilter(void)
{
if(f_sum) delete[] f_sum;
if(f_sum2) delete[] f_sum2;
if(buff) delete[] buff;
if(buff2) delete[] buff2;
}
void Boxfilter::init(int width, int height, int mwidth, int mheight)
{
this->mwidth = mwidth;
this->mheight = mheight;
this->width = width;
this->height = height;
boxwidth = width - mwidth;
boxheight = height - mheight;
f_sum = new int[boxwidth *boxheight];
f_sum2 = new int[boxwidth *boxheight];
buff = new int[width];
buff2= new int[width];
}
void Boxfilter::boxfilter (unsigned char* img)
{
int j,x,y;
memset(buff, 0, width *sizeof(int));
memset(buff2, 0, width *sizeof(int));
memset(f_sum, 0, boxwidth *boxheight);
memset(f_sum2, 0, boxwidth *boxheight);
for(y=0; ymheight/2 && ymwidth/2 && xmheight/2 && ymwidth/2 && x mheight ? mwidth : mheight;
} 测试程序
// cv2.4 test.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "opencv2/opencv.hpp"
#include "Boxfilter.h"
#include
using namespace cv;
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
Mat src = imread("C:\\Documents and Settings\\Administrator\\桌面\\img1.png",0);
Boxfilter box;
box.init(src.cols, src.rows, 5, 5);
box.boxfilter((uchar*)src.data);
int x = 50, y = 50;
float a = box.getMean(x, y); //求出以(x,y)为中心的矩形的均值
float b = box.getVar(x, y);
int c = box.getSum(x, y);
int d = box.getSquareSum(x, y);
int e = box.getLocalSize();
cout<<"mean: " < 参考
[1]: 极限优化:Haar特征的另一种的快速计算方法—boxfilter