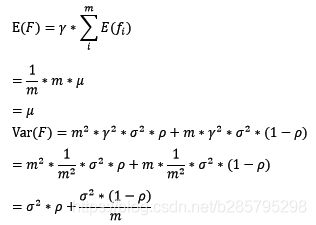【ML】随机森林(Random Forest) 从入门到放弃再到掌握

目录

集成学习

决策树

Boosting

Adaboost

GBDT

梯度提升决策树是属于boosting集成学习的一种方法，通过构建多颗CART回归树，每一轮利用上一轮学习器的残差进行树的创建。该残差使用LossFunction的负梯度进行拟合。

XGBoost对GBDT的提升

LGB对XGB的提升

Bagging

随机森林简介

随机森林构建

python中使用随机森林

为什么选决策树作为基分类器

 

偏差和方差

总结一下GBDT和RF的区别：

Random Forest和Gradient Tree Boosting参数详解

 

---

 

集成学习

让我们先看看集成学习基础理论

集成学习的主要思路是先通过一定的规则生成多个学习器，再采用某种集成策略进行组合，最后综合判断输出最终结果。一般而言，通常所说的集成学习中的多个学习器都是同质的"弱学习器"。基于该弱学习器，通过样本集扰动、输入特征扰动、输出表示扰动、算法参数扰动等方式生成多个学习器，进行集成后获得一个精度较好的"强学习器"。具有代表性的集成学习方法有Boosting，Bagging。(百度百科)

事实上,即使每一个分类器都是一个弱学习器(意味着它们也就比瞎猜好点),集成后仍然是一个强学习器(高准确率),只要有足够数量的弱学习者。

这很容易解释,假设一个不均匀的硬币,抛出它得到正面的概率为51%,得到反面的概率为49%,根据大数定律,你抛出1000次之后,得到正面的次数会差不多510次,反面的次数差不多490次.这表明纵使你的学习器很弱,精度只比瞎猜高一点点,只要你的学习器足够多,最终结果也会是优秀的。

 

接下来让我们先了解一下 决策树算法

决策树

详细决策树算法可参考我的文章:决策树（decesion Tree）从入门到放弃再到掌握

我们知道剪枝可以防止过拟合,从而提升决策树的性能,剪枝的灵活度很大,换句话说,剪枝的结果稳定性不够.数据样本的扰动对于决策树的影响较大。于是我们可以通过(1)调整树的高度来调整和改变决策树的表达能力和泛化能力,(2)通过构建不同的字样本集合训练决策树,得到的随机性更大的基分类器(3)通过随机选择特征子集,进而找出该子集中的最优分裂属性。总之,随机性的存在意味着决策树可以成为集成学习中很好的基分类器。

 

让我们回头看看集成学习的两种类型

集成学习利用的是基学习器按不同策略组合成强学习器的思想.主要有Boosting（比如GBDT） 和 bagging (比如随机森林)两类方法。

Boosting

boosting采用串行的方式,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。

 

Adaboost

代表性的Adaboost 算法:

• 第一个分类学习器被训练之前,所有样本的权重设为1/m。

• 计算第j个学习器的权重误差率(分类错误的比率)为:,其中 是第j个分类器对第i个样本的预测。很显然,分类器准确率越高,它的权重就越高。

• 计算分类器权重:。

• 按照如下公式计算新的分类器权重:

•  

• 按照以上步骤迭代训练分类器,当规定的分类器数量达到或者最好的分类器被找到后算法就会停止。

 

GBDT

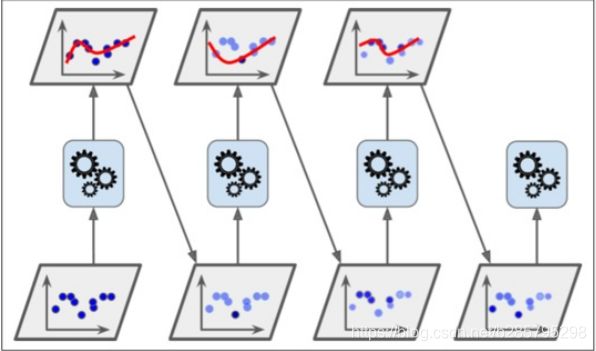
第二个代表性的算法:GBDT(Gradient Boosting Decision Tree),每次去使用新的分类器去拟合前面分类器预测的残差 。

梯度提升决策树是属于boosting集成学习的一种方法，通过构建多颗CART回归树，每一轮利用上一轮学习器的残差进行树的创建。该残差使用LossFunction的负梯度进行拟合。

一个GBDT的训练和预测过程如下:

from sklearn.tree import DecisionTreeRegressor
#训练第一个基学习器
tree_reg1 = DecisionTreeRegressor(max_depth=2)
tree_reg1.fit(X, y)
#基于残差训练第二个基学习器
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2)
tree_reg2.fit(X, y2)
#训练第三个基学习器
y3 = y2 - tree_reg1.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2)
tree_reg3.fit(X, y3)

#每一个学习器预测结果累加
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))

GBDT在分布稠密的数据集上,泛化能力和表达能力都很好,不需要对数据进行特殊的预处理如归一化,但在高维稀疏的数据集上,表现不如支持向量机或者神经网络,训练过程是串行训练,效率不高。

XGBoost对GBDT的提升

XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进。

• 传统的GBDT采用CART作为基分类器,XGBoost还支持多种类型的基分类器,比如线性分类器。在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。

• 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机森林相似的策略(列采样),支持对数据进行采样。

• 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺失值的处理策略。xgboost根据左右子节点的增益大小将缺失值分到增益大的节点中。

• 二阶泰勒展开与树正则化推出了新的叶子节点输出的计算公式而不是原始gbdt那样的简单平均；

• 分裂的时候自动根据是否产生正增益指导是否进行分裂，因为引入了正则项的概念，分裂的时候这个预剪枝更加严苛；

LGB对XGB的提升

LGB在论文主要提到的是用两种方式GOSS和EFB，提高了模型的训练速度，同时也带来了对稀疏数据的优化等提升

1.GOSS（Gradient-based One-Side Sampling）

lgb的核心思想是加速模型的训练，为了加速训练，比较直觉的想法就是减少data或者减少feature。GOSS就是对数据进行采样，来减少data。

采样的策略是：梯度越大的数据，在信息增益的计算中的影响越大，所以保存这一部分数据，而对梯度小的数据进行采样。将数据的梯度计算之后进行排序，选择最大的topN，然后再对剩下的梯度较小的数据进行随机采样。为了不改变训练数据的分布，对于采样之后的小梯度数据，再乘以一个系统fact。

通过理论和实验分析，都可以证明这种采样能够不影响模型的准确率，并且比直接的随机采样效果更出众。采样还引入的随机性，使模型提高的泛化能力。

2.EFB（Exclusive Feature Bundling）

前面说到加速训练的直觉想法就是减少data或者feature，提出的第二个方法就是减少feature，同时也是对稀疏特征的优化。论文提到，采用预排序的方法可以忽略零值来处理稀疏特征，直方图算法因为要遍历所有的 特征值进行分箱，所以之前没有很好的策略对直方图算法进行处理稀疏特征的优化，EFB就起到了这个效果。

EFB的策略就是：对于很少同时出现非零值的特征，称之为互斥特征（Exclusive Feature），这样的特征可以绑定在一起，以减少特征的数量，减少直方图构建的时间复杂度。这种绑定是一个NP难得问题，将它转化为一个图着色的问题，以其中每个节点的度作为指标进行排序，可以采用贪心策略获得一个局部最优解。

其中有一个参数是γ，是最大的冲突程度。因为大多数特征不是百分百互斥或者说绝对互斥，γ的意思就是一定程度允许互斥特征偶尔会同时出现非零值。γ使得绑定特征有一定的污染，会影响准确率，但能够更多的减少特征，加快模型训练，所以是一个时间和准确率的平衡。

但是当特征非常多的时候，构件图也是一个很费时的事情，因为构建一个图的时间复杂度是特征数量的平方，所有又给了一种替换方法，就是以特征的非零值数量作为指标进行排序，因为非零值越多，越容易产生大的冲突。

 

Bagging

bagging ( bootstrap aggregating 的缩写)是并行的方法,它可以 (1) 使用相同的算法在不同的训练集上面训练多个基学习器,也可以(2) 使用不同的训练算法训练得到多个基学习器。

当所有的分类器被训练后,集成可以通过对所有分类器结果的简单聚合来对新的实例进行预测。聚合函数通常对分类是统计模式(例如硬投票分类器)或者对回归取平均。

 

随机森林简介

随机森林（Random Forest）是Bagging的一个扩展变体。其在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择，即：传统决策树在选择划分属性时是在当前结点的属性集合中（假设共有d个结点）基于信息纯度准则等选择一个最优属性，而在随机森林中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，再对该子集进行基于信息准则的划分属性选择；这里的k控制了随机性的引入程度；若令k=d，则基决策树的构建与传统决策树相同；若令k=1，则每次的属性选择纯属随机，与信息准则无关；一般情况下，推荐k=log2d。

随机森林构建

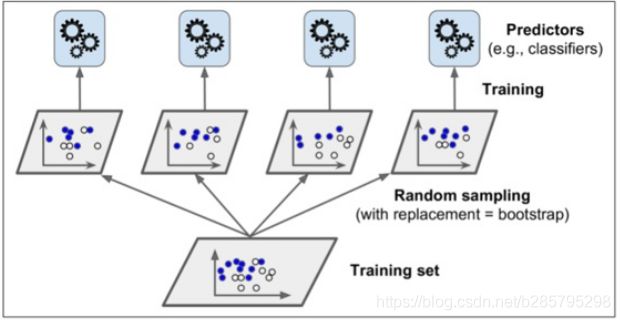
我们知道Bagging方法的思路之一就是从样本集中使用bootstrap 采样来训练多个学习器,最后将这些学习器的能力集成起来。随机森林也是如此。构建RF的步骤如下:

1. 随机且有放回地从训练集中的抽取N个训练样本（bootstrap sample）,作为某棵树的训练集；

2. 如果每个样本的特征维度为M，指定一个常数m<m个特征子集；

3. 每次树进行分裂时，从这m个特征中选择最优划分特征, 每棵树都尽最大程度的生长，并且没有剪枝过程。

4. 重复上述步骤建立多棵树(基分类器)；

 

RF的最大特点就是引入了随机性,在构建过程中,m的选择很关键,若m= M, 则基决策树的构建与传统的决策树相同,若m =1 ,则表示随机选择一个属性用于划分,一般选取m = log2M。

 

python中使用随机森林

>>>from sklearn.ensemble import RandomForestClassifier
>>>rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1)
>>>rnd_clf.fit(X_train, y_train)
>>>y_pred_rf = rnd_clf.predict(X_test)

为什么选决策树作为基分类器

正如我们之前讲的,决策树有很好的随机性。这也是为什么决策树经常被拿来作基学习器的原因,除决策树之外,神经网络也有类似的性质。当然任何分类模型都可以作为基分类器。但随机森林中最好还是用决策树。随机森林属于Bagging类的集成学习。Bagging所采用的基分类器,最好是本身对样本分布较为敏感的(即所谓不稳定的分类器),如线性分类器或者KNN都是较为稳定的分类器,本身方差(Variance)就不大,所以以它们为基分类器使用Bagging并不能在原有基分类器的基础上获得更好的表现,甚至可能因为Bagging的采样,而导致他们在训练中更难收敛,从而增大了集成分类器的偏差(Bias)。

 

偏差和方差

参考自：https://www.cnblogs.com/jasonfreak/p/5657196.html

 

说明
偏差指的是所有模型的输出的平均值和真实模型输出之间的偏差。
方差指的是所有模型的输出结果彼此之间的分散程度。

 

模型的偏差是一个相对来说简单的概念：训练出来的模型在训练集上的准确度。（模型在训练集上准确度越高，偏差越小，但此时的模型也有可能完全“拟合”当前的数据，而丧失泛化能力（过拟合））

研究模型的方差有什么现实的意义呢？我们认为方差越大的模型越容易过拟合：

假设有两个训练集A和B，经过A训练的模型Fa与经过B训练的模型Fb差异很大，这意味着Fa在类A的样本集合上有更好的性能，而Fb反之，这便是我们所说的过拟合现象。

 

 

下文解释了为什么Bagging降方差（因为基模型是强模型），Boosting降偏差（基模型是弱模型）？

我们常说集成学习框架中的基模型是弱模型，通常来说弱模型是偏差高（在训练集上准确度低）方差小（防止过拟合能力强）的模型。但是，并不是所有集成学习框架中的基模型都是弱模型。bagging和stacking中的基模型为强模型（偏差低方差高），boosting中的基模型为弱模型。

bagging的偏差和方差：

根据上式我们可以看到，整体模型的期望 近似于 基模型的期望，这也就意味着整体模型的偏差 和 基模型的偏差近似。同时，整体模型的方差小于等于基模型的方差（当相关性为1时取等号），随着基模型数（m）的增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。但是，模型的准确度一定会无限逼近于1吗？并不一定，当基模型数增加到一定程度时，方差公式第二项的改变对整体方差的作用很小，防止过拟合的能力达到极限，这便是准确度的极限了。另外，在此我们还知道了为什么bagging中的基模型一定要为强模型，否则就会导致整体模型的偏差度低，即准确度低。

　　Random Forest是典型的基于bagging框架的模型，其在bagging的基础上，进一步降低了模型的方差。Random Fores中基模型是树模型，在树的内部节点分裂过程中，不再是将所有特征，而是随机抽样一部分特征纳入分裂的候选项。这样一来，基模型之间的相关性降低，从而在方差公式中，第一项显著减少，第二项稍微增加，整体方差仍是减少。

 

　对于boosting来说，基模型的训练集抽样是强相关的，那么模型的相关系数近似等于1，故我们也可以针对boosting化简公式为：

 

通过观察整体方差的表达式，我们容易发现，若基模型不是弱模型，其方差相对较大，这将导致整体模型的方差很大，即无法达到防止过拟合的效果。因此，boosting框架中的基模型必须为弱模型。

　　因为基模型为弱模型，导致了每个基模型的准确度都不是很高（因为其在训练集上的准确度不高）。随着基模型数的增多，整体模型的期望值增加，更接近真实值，因此，整体模型的准确度提高。但是准确度一定会无限逼近于1吗？仍然并不一定，因为训练过程中准确度的提高的主要功臣是整体模型在训练集上的准确度提高，而随着训练的进行，整体模型的方差变大，导致防止过拟合的能力变弱，最终导致了准确度反而有所下降。

基于boosting框架的Gradient Tree Boosting模型中基模型也为树模型，同Random Forrest，我们也可以对特征进行随机抽样来使基模型间的相关性降低，从而达到减少方差的效果。

 

总结一下GBDT和RF的区别：

GBDT属于boosting类集成学习，基学习器一般为CART回归树，bagging中的基模型一定要为强模型（偏差小，方差大），否则就会导致整体模型的偏差度低，即准确度低。随着基模型数的增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。

RF属于bagging类集成学习，基学习器一般为决策树，在树的内部节点分裂过程中，不再是将所有特征，而是随机抽样一部分特征纳入分裂的候选项。因为基模型为弱模型（偏差大，方差小），导致了每个基模型的准确度都不是很高（因为其在训练集上的准确度不高）。随着基模型数的增多，整体模型的期望值增加，更接近真实值，因此，整体模型的准确度提高。

 

 

Random Forest和Gradient Tree Boosting参数详解

（参考自:https://www.cnblogs.com/jasonfreak/p/5720137.html）

　　还记得调参的目标吗：模型在训练集上的准确度和防止过拟合能力的大和谐！为此，我们目前做了一些什么工作呢？

1. 使用模型的偏差和方差来描述其在训练集上的准确度和防止过拟合的能力

2. 对于bagging来说，基模型是强模型，整体模型的偏差和基模型近似，随着训练的进行，整体模型的方差降低

3. 对于boosting来说，基模型为弱模型，整体模型的初始偏差较高，方差较低，随着训练的进行，整体模型的偏差降低（虽然也不幸地伴随着方差增高），当训练过度时，因方差增高，整体模型的准确度反而降低

4. 整体模型的偏差和方差与基模型的偏差和方差息息相关

　　这下总算有点明朗了，那些让我们抓狂的参数，现在可以粗略地分为两类了：控制整体训练过程的参数和基模型的参数，这两类参数都在影响着模型在训练集上的准确度以及防止过拟合的能力。

 

不难发现，基于bagging的Random Forest模型和基于boosting的Gradient Tree Boosting模型有不少共同的参数，然而某些参数的默认值又相差甚远。Random Forest的子模型都拥有较低的偏差，整体模型的训练过程旨在降低方差，故其需要较少的子模型（n_estimators默认值为10）且子模型不为弱模型（max_depth的默认值为None），同时，降低子模型间的相关度可以起到减少整体模型的方差的效果（max_features的默认值为auto）。

另一方面，Gradient Tree Boosting的子模型都拥有较低的方差，整体模型的训练过程旨在降低偏差，故其需要较多的子模型（n_estimators默认值为100）且子模型为弱模型（max_depth的默认值为3），但是降低子模型间的相关度不能显著减少整体模型的方差（max_features的默认值为None）。

 

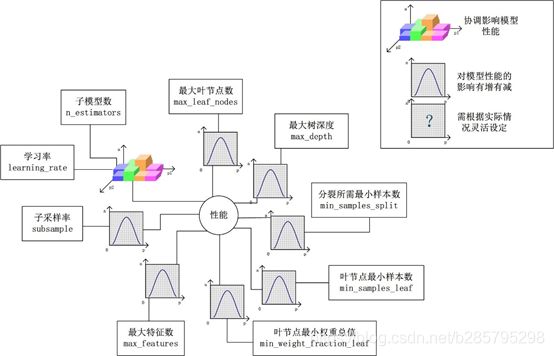
这些参数又可分为两类：过程影响类及子模型影响类。在子模型不变的前提下，某些参数可以通过改变训练的过程，从而影响模型的性能，诸如：“子模型数”（n_estimators）、“学习率”（learning_rate）等。另外，我们还可以通过改变子模型性能来影响整体模型的性能，诸如：“最大树深度”（max_depth）、“分裂条件”（criterion）等。正由于bagging的训练过程旨在降低方差，而boosting的训练过程旨在降低偏差，过程影响类的参数能够引起整体模型性能的大幅度变化。一般来说，在此前提下，我们继续微调子模型影响类的参数，从而进一步提高模型的性能。

参数对整体模型性能的影响

假设模型是一个多元函数F，其输出值为模型的准确度。我们可以固定其他参数，从而对某个参数对整体模型性能的影响进行分析：是正影响还是负影响，影响的单调性？

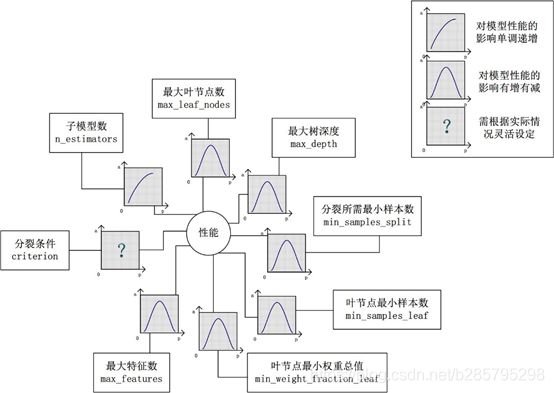
　　对Random Forest来说，增加“子模型数”（n_estimators）可以明显降低整体模型的方差，且不会对子模型的偏差和方差有任何影响。模型的准确度会随着“子模型数”的增加而提高。由于减少的是整体模型方差公式的第二项，故准确度的提高有一个上限。在不同的场景下，“分裂条件”（criterion）对模型的准确度的影响也不一样，该参数需要在实际运用时灵活调整。调整“最大叶节点数”（max_leaf_nodes）以及“最大树深度”（max_depth）之一，可以粗粒度地调整树的结构：叶节点越多或者树越深，意味着子模型的偏差越低，方差越高；同时，调整“分裂所需最小样本数”（min_samples_split）、“叶节点最小样本数”（min_samples_leaf）及“叶节点最小权重总值”（min_weight_fraction_leaf），可以更细粒度地调整树的结构：分裂所需样本数越少或者叶节点所需样本越少，也意味着子模型越复杂。一般来说，我们总采用bootstrap对样本进行子采样来降低子模型之间的关联度，从而降低整体模型的方差。适当地减少“分裂时考虑的最大特征数”（max_features），给子模型注入了另外的随机性，同样也达到了降低子模型之间关联度的效果。但是一味地降低该参数也是不行的，因为分裂时可选特征变少，模型的偏差会越来越大。在下图中，我们可以看到这些参数对Random Forest整体模型性能的影响：

对Gradient Tree Boosting来说，“子模型数”（n_estimators）和“学习率”（learning_rate）需要联合调整才能尽可能地提高模型的准确度：想象一下，A方案是走4步，每步走3米，B方案是走5步，每步走2米，哪个方案可以更接近10米远的终点？同理，子模型越复杂，对应整体模型偏差低，方差高，故“最大叶节点数”（max_leaf_nodes）、“最大树深度”（max_depth）等控制子模型结构的参数是与Random Forest一致的。类似“分裂时考虑的最大特征数”（max_features），降低“子采样率”（subsample），也会造成子模型间的关联度降低，整体模型的方差减小，但是当子采样率低到一定程度时，子模型的偏差增大，将引起整体模型的准确度降低。还记得“初始模型”（init）是什么吗？不同的损失函数有不一样的初始模型定义，通常，初始模型是一个更加弱的模型（以“平均”情况来预测），虽说支持自定义，大多数情况下保持默认即可。在下图中，我们可以看到这些参数对Gradient Tree Boosting整体模型性能的影响：

 

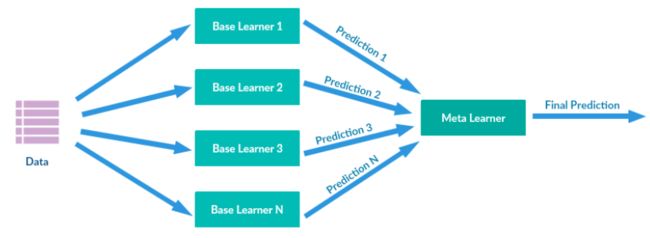
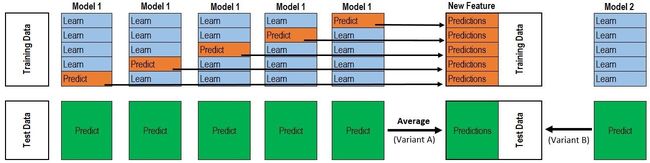
stacking

Stacking是许多集成方法的综合。其主要思路如下图所示，通过训练数据训练多个base learners（the first-level learners），这些learners的输出作为下一阶段meta-learners（the second-level learners）的输入，最终预测由meta-learners预测结果得到。

一些现成的stacking的框架的链接：
https://github.com/liyi19950329/stacking
https://github.com/mpearmain/gestalt
https://github.com/reiinakano/xcessiv
https://github.com/kaz-Anova/StackNet
https://github.com/liyi19950329/vecstack
https://github.com/liyi19950329/mlens
https://github.com/rasbt/mlxtend

 

 

向您推荐我的其他文章:

支持向量机（SVM）从入门到放弃再到掌握 :https://blog.csdn.net/b285795298/article/details/81977271

逻辑回归(Logistic Regression-LR)从入门到放弃再到掌握 :https://blog.csdn.net/b285795298/article/details/88683987

决策树（decesion Tree）从入门到放弃再到掌握 :https://blog.csdn.net/b285795298/article/details/89086854

随机森林(Random Forest) 从入门到放弃再到掌握:https://blog.csdn.net/b285795298/article/details/89084257