GraphRNN: Generating Realistic Graphs with Deep Auto-regressive Models 使用深度自回归模型生成现实中的图

原文链接:https://arxiv.org/abs/1802.08773
更多细节:Stanford CS224W:Machine Learning with Graphs

摘要

图的建模和生成是研究生物学、工程学和社会科学网络的基础。然而，由于图的非唯一性、高维性以及给定图的边之间存在的复杂的非局部依赖性，对图上的复杂分布进行建模，然后从这些分布中有效地采样是一项挑战。作者提出了名为GraphRNN的的深度自回归模型，它可以解决上述挑战并且以最小的结构假设逼近任何图的分布。GraphRNN通过对一组有代表性的图进行训练来学习生成图，并且将图的生成过程分解为一连串的节点和边的生成。为了定量评估GraphRNN的性能，作者引入了基准数据集，基线和基于最大平均差异的新的评估指标，这些指标衡量图集之间的距离。作者的实验证明GraphRNN显著优于所有基线，能学习生成符合目标集结构特征的各种图，同时可以扩展到比以前的深度模型大50倍的图。

1.介绍

传统的图生成模型是针对特定的图簇进行建模而设计的，无法直接从观测数据中学习生成模型。而变分自动编码器（VAE）和生成对抗网络（GAN）等深度生成模型，在图像和文本数据等复杂领域的生成建模方面取得了重要进展。在上述这些方法的基础上，有研究人员提出了一些用于生成图的深度学习模型，然而，这些深度模型要么仅限于从单个图中学习，要么生成仅包含40个或更少节点的小图，上述这些限制源于图生成问题中三个挑战：

• 大规模和可变的输出空间：生成模型必须输出 $n^2$ 个值来完全确定具有 $n$ 个结点的图的结构。此外，不同的图的节点数 $n$ 和 边数 $m$ 也不同，生成模型需要在输出空间中适应这种复杂性和变化性。
• 不唯一的表示：在一般的图生成问题中，希望对可能的图结构进行分布，而不假设固定的节点集。在这种一般情况下，一个有 $n$ 个节点的图可以由多达 $n!$ 个等价的邻接矩阵来表示，每个矩阵对应于不同的、任意的节点排序/编号。如此高的表示复杂度对建模来说是个挑战，并使得在训练期间计算和优化目标函数成本很高。
• 复杂依赖：图中的边形成涉及复杂的结构依赖性。例如，在许多现实世界的图中，如果两个节点有共同的邻居，它们就更有可能被连接起来。因此，边的生成不是一连串独立的事件，而是需要联合生成，其中每下一条边的生成都取决于之前生成的边。

2.贡献

• 作者解决了上述挑战，提出了GraphRNN，一个用于学习图生成模型的可扩展的框架。GraphRNN以自回归（或递归）的方式对图进行建模，来捕捉图中所有节点和边的复杂联合概率。特别的是，GraphRNN可以被看做是一个分层模型，其中一个图级的RNN保持图的状态并生成新的节点，而一个边级RNN为每一个新生成的节点生成边。
• 作者引入了广度优先搜索（BFS）的节点排序方案来大幅度提高可扩展性。这种BFS方法通过将不同的表征折叠成唯一的BFS树，缓解了图具有非唯一表征的事实，而且BFS引起的树状结构允许使用者在训练期间限制每个节点的边预测的数量。
• 作者提供了一个全面的评估设定，即通过比较两组图形的度分布、聚类系数分布和基于最大平均差异（MMD）的变体的图案计数。这种定量评估方法可以比较图统计分布的高阶矩，并提供比简单比较平均值更严格的评价。

3.符号和问题定义

一个无向图 $G=(V,E)$ 是通过它的节点集 $V=\{V_1,...,V_n\}$ 和边集 $E=\{(v_i,v_j)|v_i,v_j\in V\}$ 来定义的。表示图的一种常见的方法是使用邻接矩阵，这需要一个节点排序 $\pi$ 将节点映射到邻接矩阵的行或列。 $\Pi$ 定义为所有 $n!$ 个可能的节点排列组合的集合。在节点排序 $\pi$ 下，图 $G$ 可以用邻接矩阵 $A^{\pi }\in {\mathbb{R}}^{n\times n}$ 表示，$A_{i,j}^{\pi }=1[(\pi (v_i,v_j))\in E]$。

学习图的生成模型的目标是基于一组从数据分布 $p(G)$ 中抽样的观察图 $\mathbb{G}=\{G_1,...G_s\}$ ，在图上学习一个分布 $p_{model}(G)$ ，其中每个图 $G_i$ 可能有不同的节点数和边数。当表示 $G\in \mathbb{G}$，进一步假设可以以相同概率观察到任何节点排序 $\pi$ ，即 $p(\pi )=\frac{1}{n!},\forall \pi \in \Pi$​ 。因此，生成模型需要能够生成图，而每个图可能有指数级的许多表示，这与以前的图像、文本和时间序列的生成模型不同。传统的图生成模型通常假定一个单一的输入训练图，作者的方法更为通用，可以应用于单个或多个输入训练图。

4.GraphRNN：图的深度生成模型

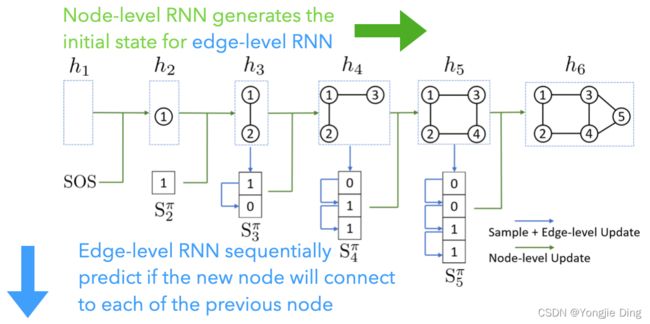
作者的方法的关键思想是将不同节点排序下的图表示为序列，然后在这些序列上建立一个自回归生成模型。正如之前所介绍的，这种方法没有其他一般方法常见的缺点，允许使用者对具有复杂边依赖关系的不同大小的图进行建模，并且引入了BFS节点排序方案，来大幅度降低对所有可能的节点序列进行学习的复杂性。在这个自回归框架中，通过与递归神经网络（RNNs）的权重共享，大幅度降低了模型的复杂性。下图说明了GraphRNN的方法，其主要思想是将图生成分解为一个通过图级RNN生成节点序列的过程，以及另一个通过边级RNN为每个新添加的节点生成边序列的过程。

4.1.将图建模为序列

首先定义一个从图到序列的映射 $f_S$ ，对于一个在节点排序 $\pi$ 下有 $n$ 个节点的图 $G\sim p(G)$ ，有
$$S^{\pi }=f_S(G,\pi )=(S_1^{\pi },...,S_n^{\pi })\text{\hspace{1em}(1)}$$
其中每个元素 $S_i^{\pi }\in \{0,1{\}}^{i-1},i\in \{1,...,n\}$ 是一个邻接向量，表示节点 $\pi (v_i)$ 和图中已有的之前的节点 $v_{(}j),j\in \{1,...,i-1\}$ 之间的边：
$$S_i^{\pi }=(A_{1,i}^{\pi },...,A_{i-1,i}^{\pi }{)}^T,\forall i\in \{2,...,n\}\text{\hspace{1em}(2)}$$
对于无向图，$S^{\pi }$ 决定了一个唯一的图 $G$ ，我们把这个映射记为 $f_G(\cdot )$ ，其中 $f_G(S^{\pi })=G$ 。

因此，不需要学习样本空间难以描述的 $p(G)$ ，而是通过对辅助 $\pi$ 进行抽样来获得 $S^{\pi }$ 的观测值，并学习 $p(S^{\pi })$ ，由于 $S^{\pi }$ 的顺序性， $p(S^{\pi })$ 可以被自回归地建模。在推导时，可以通过采样 $S^{\pi }$ 对 $G$ 进行采样，而不用明确地计算 $p(G)$ ， $S^{\pi }$ 通过 $f_G$ 映射到 $G$。

给定上述定义，可以将 $p(G)$ 写为联合分布 $p(G，S^{\pi })$ 的边缘分布：
$$p(G)=\sum _{S^{\pi }}p(S^{\pi })1[f_G(S^{\pi })=G],\text{\hspace{1em}(3)}$$
其中 $p(S^{\pi })$ 是想通过生成模型来学习的分布。由于 $S^{\pi }$ 的顺序性，进一步将 $p(S^{\pi })$ 分解为各元素的条件分布的乘积：
$$p(S^{\pi })=\prod _{i=1}^{n+1}p(S_i^{\pi }|S_1^{\pi },...,S_{i-1}^{\pi })\text{\hspace{1em}(4)}$$
其中，将 $S_{n+1}^{\pi }$ 设为序列的结束标记EOS，来表示长度可变的序列。在进一步讨论中，将 $p(S_i^{\pi }|S_1^{\pi },...,S_{i-1}^{\pi })$ 简化为 $p(S_i^{\pi }|S_{<i}^{\pi })$ 。

4.2.GraphRNN的框架

到目前为止，已经将 $p(G)$ 的建模转化为对 $p(S^{\pi })$ 的建模，作者进一步将 $p(S^{\pi })$ 分解为条件概率 $p(S_i^{\pi }|S_{<i}^{\pi })$ 。请注意， $p(S_i^{\pi }|S_{<i}^{\pi })$ 是非常复杂的，因为它必须根据以前的节点之间的相互连接方式来捕捉节点 $\pi (v_i)$ 与以前的节点之间的联系。这里作者提出用神经网络对复杂分布建模来参数化 $p(S_i^{\pi }|S_{<i}^{\pi })$ 。为了实现可扩展的建模，作者让神经网络在所有的时间步骤 $i$ 中共享权重。特别的，作者使用由一个状态转换函数和一个输出函数组成的RNN：
$$h_i=f_{trans}(h_{i-1},S_{i-1}^{\pi })\text{\hspace{1em}(5)}$$$${\theta }_i=f_{out}(h_i)\text{\hspace{1em}(6)}$$
其中 $h_i\in {\mathbb{R}}^d$ 是一个编码到目前为止所生成的图的状态的向量，$S_{i-1}^{\pi }$ 是最新生成的节点 $i-1$ 的邻接向量，而 ${\theta }_i$ 则指定了下一个节点的邻接向量的分布（如 $S_i^{\pi }\sim {\mathcal{P}}_{{\theta }_i}$）。一般来说，$f_{trans}$ 和 $f_{out}$ 可以是任意的神经网络，而 $P_{{\theta }_i}$ 可以是二进制向量上的任意分布。下图算法是对这个总体框架的总结。

请注意，上述关于问题表述是完全通用的，在之后的讨论中将提出一些具体的变化并提供实施细节。同时，RNN需要固定大小的输入向量，而之前定义 $S_i^{\pi }$ 有不同的的尺寸且取决于 $i$ ，在之后将描述一个有效且灵活的方案来解决这个问题。

4.3.GraphRNN变量

GraphRNN的不同变量对应于关于 $p(S_i^{\pi }|S_{<i}^{\pi })$ 的不同假设。$S_i^{\pi }$ 的每个维度都是一个二进制值，用来模拟新节点 $\pi (v_i)$ 和之前节点 $\pi (v_j),j\in \{1,...,i-1\}$ 之间是否存在一条边。

多变量伯努利 首先，作者提出一个简单的GraphRNN方法的基线变体，称之为GraphRNN-S。在这个变体中，作者将 $p(S_i^{\pi }|S_{<i}^{\pi })$ 建模为多变量伯努利分布，由 $f_{out}$ 所输出的 ${\theta }_i\in {\mathbb{R}}^{i-1}$ 向量作为参数。特别是，作者将 $f_{out}$ 实现为在所有时间步骤中共享权重的，具有sigmoid激活函数的单层多层感知器（MLP）。$f_{out}$ 的输出是向量 ${\theta }_i$ ，其元素 ${\theta }_i[j]$ 可以解释为边 $(i,j)$ 的概率。然后根据由 ${\theta }_i$参数化的多变量伯努利分布对 $S_i^{\pi }$ 中的边进行独立抽样。

依赖的伯努利序列 为了充分捕捉复杂的边依赖关系，在完整的GraphRNN模型中，作者进一步将 $p(S_i^{\pi }|S_{<i}^{\pi })$ 分解为条件的乘积，
$$p(S_i^{\pi }|S_{<i}^{\pi })=\prod _{j=1}^{i-1}p(S_{i,j}^{\pi }|S_{i,<j}^{\pi },S_{<i}^{\pi })\text{\hspace{1em}(7)}$$
其中 $S_{i,j}^{\pi }$ 在节点 $\pi (v_{i+1})$ 与节点 $\pi (v_j)$ 相连的时候表示一个二进制的标量1。在这个变体中，乘积中的每一个分布都是由另一个RNN近似得来。在概念上，有一个分层RNN，其中第一个（图级）RNN生成节点并保持图的状态，而第二个（边级）RNN生成给定节点的边。在作者的实现中，边级RNN是一个GRU模型，其中隐藏状态通过图级隐藏状态 $h_i$ 初始化，其中每一步的输出都由MLP映射到一个标量上表示存在一条边的概率。$S_{i,j}^{\pi }$ 从第 $i$ 个边级RNN的第 $j$ 个输出指定的分布中采样，并被送入同一个RNN的第 $j+1$ 个输入。所有的边级RNN共享相同的参数。

4.4.通过广度优先搜索实现可操作性

在作者的方法中，不是学习在任何可能的节点序列下生成图，而是通过学习使用广度优先搜索（BFS）的节点序列来生成图，且这种方法不局限于生成某类特定图集的图，具有更好的通用性。形式上，作者将式（1）修改为：
$$S^{\pi }=f_S(G,BFS(G,\pi ))\text{\hspace{1em}(8)}$$
其中，$BFS(\cdot )$ 表示确定的BFS函数。 具体来说，这个BFS函数以随机排列组合 $\pi$ 作为输入，选取 $\pi (v_1)$ 作为起始节点，按照 $\pi$ 定义的顺序将节点的邻居加入到BFS序列中。请注意，BFS函数是多对一的，即，在应用BFS函数后，多个排列组合可以映射到相同的序列。

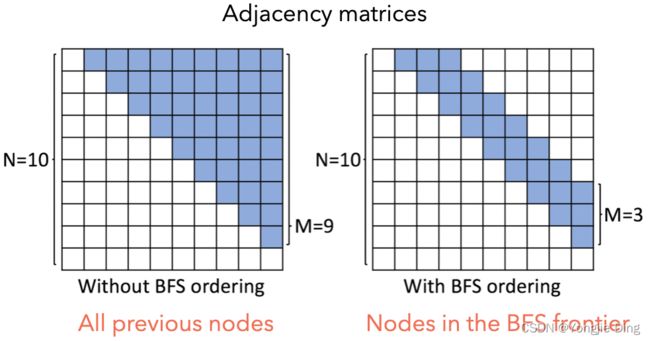
在生成过程中使用BFS来指定节点排序有两个基本的好处。首先，只需要训练所有可能的BFS排序，而不是所有可能的节点排序，即多个节点排序映射到相同的BFS排序，从而减少了需要考虑的序列的总数量。其次，BFS排序通过减少在边级RNN上对边的预测的数量来使学习更简单；特别是，当在BFS排序下增加一个新节点时，这个新节点唯一可能的边是那些连接到BFS "前沿 "的节点（即仍在BFS队列中的节点）一个由命题1正式确定的概念。是否使用BFS排序如下图所示。

命题1.假设 $v_1,...,v_n$ 是图 $G$ 中 $n$ 个结点的BFS排序，对于部分 $i<j\le n$，$(v_i,v_{j-1})\in E$ 但 $(v_i,v_j)\notin E$ ，那么 $(v_{i^{\prime }},v_{j^{\prime }})\notin E,\forall 1\le i^{\prime }\le i,j\le j^{\prime }\le n$ 。

重要的是，这一使用能够将可变大小的 $S_i^{\pi }$ 向量重新定义为一个固定的 $M$ 维向量，代表节点 $\pi (v_i)$ 与当前队列中BFS最大大小为 $M$ 的节点之间的连接性：
$$S_i^{\pi }=(A_{max(1,i-M),i}^{\pi },...,A_{i-1,i}^{\pi }{)}^T,i\in \{2,...,n\}.\text{\hspace{1em}(9)}$$

5.实验

作者在合成数据集和真实数据集上进行了实验，这些数据集的大小和特征都有很大的不同。图的大小从 |V| = 10到 |V| = 2025不等。同时将模型的性能与各种传统的图生成模型以及最近的一些深度图生成模型进行比较。

5.1.评估生成图

本案例中，评估需要在两组图形（生成的图形和测试集）之间进行比较。以前的工作依赖于定性的视觉检查或两组之间平均统计数据的简单比较，而作者提出了新的评价指标，比较其经验分布的所有时刻。作者提出的度量标准是基于最大平均差异（MMD）的度量。假设用再现核Hilbert空间 $\mathcal{H}$ 中的一个单位球作为其函数类 $\mathcal{F}$ ，$k$ 是相关的核，来自分布 $p$ 和分布 $q$ 的两组样本之间的MMD平方可以得出

$$MM{D}^2(p||q)={\mathbb{E}}_{x,y\sim p}[k(x,y)]+{\mathbb{E}}_{x,y\sim q}[k(x,y)]-2{\mathbb{E}}_{x\sim p,y\sim q}[k(x,y)]\text{\hspace{1em}(10)}$$
一般来说，图上适当的距离度量是难以计算的。因此，作者使用一组图统计量 $\mathbb{M}=\{M_1,...,M_k\}$ 来计算MMD，其中每个 $M_i(G)$ 是 $\mathbb{R}$ 上的一个单变量分布，如度分布或聚类系数分布。然后，作者使用第一个Wasserstein距离作为两个分布 $p$ 和 $q$ 之间的有效距离度量：
$$W(p,q)=\underset{\gamma \in \prod (p,q)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]\text{\hspace{1em}(11)}$$
其中 $\prod (p,q)$ 是边际分别为 $p$ 和 $q$ 的所有分布的集合，使用下面的核，其泰勒展开是所有时刻的线性组合：

命题2.由 $k_W(p,q）=\exp \frac{W(p,q)}{2{\sigma }^2}$ 定义的核函数induces了唯一的***RKHS*** 。

在实验中，作者展示了这个导出的MMD分数的度数和聚类系数分布，以及平均轨道计数统计，即所有有4个节点的轨道的出现次数。作者使用RBF核来计算计数向量之间的距离。

5.2.生成高质量图

图可视化 下图显示了GraphRNN和各种基线生成的图形，表明GraphRNN能够捕捉具有巨大差异的数据集的结构，能够有效地学习像网格这样的常规结构，以及像Ego网络这样的更自然的结构。具体来说，可以发现GraphRNN生成的网格并没有出现在训练集中，也就是说，它学会了对未见过的网格宽度/高度进行归纳。

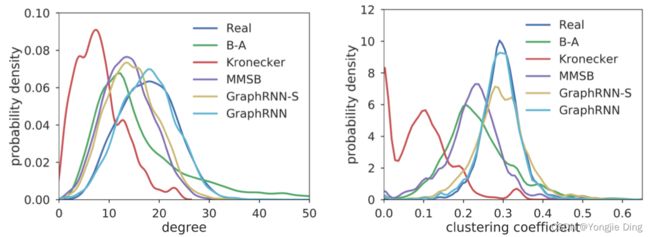
用图形统计学进行评估 作者使用三种基于度数、聚类系数和轨道计数的图统计来进一步定量评估生成的图。下图显示了测试图与生成图中的平均图统计量，这表明即使从数百个不同大小的图中，GraphRNN仍然可以很好地学习捕获基本的图统计量，生成的平均统计量与整个测试集的分布密切匹配。

下表分别总结了对完整数据集和小版本的MMD评估。作者用固定的步骤训练所有的模型，并在训练误差最小的步骤报告测试集的性能。GraphRNN变体在所有数据集上都取得了最好的性能，与传统基线相比，MMD平均下降了80%，与深度学习基线相比，MMD下降了90%。有趣的是，在蛋白质数据集上，更简单的GraphRNN-S模型表现非常好，这可能是由于蛋白质数据集是欧氏空间的近邻图，因此不涉及高度复杂的边缘依赖关系。请注意，一些基线模型在特定的数据集上表现良好，但它们不能在其他类型的输入图上通用。

归纳能力 上表同时显示了训练集和测试集上的负对数似然（NLLs）。一个具有良好泛化能力的模型应该在训练图和测试图之间有很小的NLL差距。可以发现，GraphRNN模型可以很好地泛化，平均NLL差距小22%。

5.3.稳定性

作者通过在B-A和E-R图之间进行插值来研究模型的稳定性。作者随机扰动有100个节点的B-A图的 [ 0%, 20%, …, 100% ] 边。在对0%的边进行扰动的情况下，这些图是E-R图；在对100%的边进行扰动的情况下，这些图是 B-A 图。下图显示了6组图形的度和聚类系数分布的MMD得分。B-A和E-R在从各自的分布中生成图形时表现良好，但一旦引入噪声，它们的性能就会明显下降。相比之下，GraphRNN在作者对这些结构进行插值时保持了强大的性能，这表明了它的高鲁棒性和通用性。

6.总结

作者提出了GraphRNN，一个针对图结构数据的自回归生成模型，以及一个针对图生成问题的综合评估套件，作者用它来证明GraphRNN与以前的先进模型相比取得了明显的性能，同时具有可扩展性和对噪声的鲁棒性。然而，这一领域仍然存在重大挑战，如扩展到更大的图，以及开发能够进行有效条件限制的图生成模型。