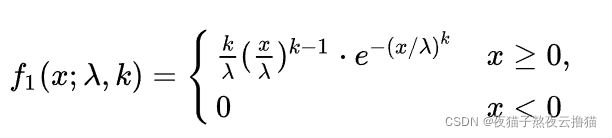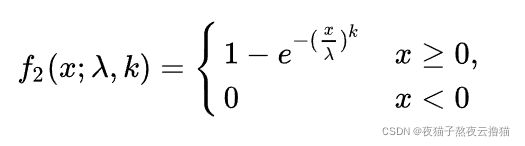开集识别(Open Set Recognition, OSR)算法:《Towards Open Set Deep Networks》OpenMax
写完了论文,重新梳理一下,以后不再更新。
1.相关论文源码
《Towards Open Set Deep Networks》即OpenMax源码:https://github.com/abhijitbendale/OSDN
《Meta-Recognition: The Theory and Practice of Recognition Score Analysis》即libMR, OpenMax使用libMR完成Weibull拟合。源码:https://github.com/Vastlab/libMR
2.极值理论
为什么使用极值理论?因为普通的分布模型不再满足实际场景下的部分情况。
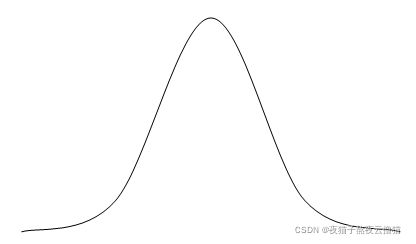
以正态分布为例,该分布模型在极值部分的分布和真实情况不符合。
图1 正态分布示意图
如图1,极值部分指的就是分布的两端部分。
因为普通的分布模型不能较好地反映极值的分布,因此出现极值理论。
目前极值理论中有三种极值分布来反映极值部分的分布情况,分别为:Gumbel分布、Frechet分布以及Weibull分布。
目前开集识别都是按照Weibull分布来应用的,尾部分布为Weibull分布的证明可以查看《Meta-Recognition: The Theory and Practice of Recognition Score Analysis》。
weibull分布的概率密度函数(pdf)为:
weibull分布的累计分布函数(cdf)为:
假设Weibull分布拟合的是图1的右端极大值 (极小值也是一样的逻辑),则weibull的累计分布函数(cdf) ![]() 指的是极大值出现在
指的是极大值出现在![]() 中的概率。
中的概率。
3.OpenMax思路
讲完了极值理论,那么OpenMax利用极值理论做什么呢?-->根据元识别的思想矫正分类得分。
元识别的思想是什么?-->以某个模型 (meta-recognition system) 判断分类模型 (也可以是其他模型,libMR论文称为recognition system)失效的概率。
所以总结来看OpenMax就是以各已知类样本拟合得到的Weibull模型 (meta-recognition system)判断闭集分类模型 (recognition system) 分类失败的概率,并以分类失败的概率矫正已知类得分+计算未知类得分。
既然OpenMax的思路已知,接下来就是两个问题需要考虑:
如何得到各已知类的Weibull模型?
2.如何借助Weibull模型矫正得分?
3.1 得到各已知类的Weibull模型
3.1.1 得到各已知类的距离集Di={D1, D2, ...., Dm}。
(1). OpenMax先训练好闭集分类网络DCNN。以第i类已知类为例,将所有第i类的训练样本输入到DCNN中得到它们的激活向量AV (Activation Vector),并保留DCNN正确分类为第i类样本的AV (即DCNN分类失败的第i类样本的AV不保留),记保留的AV集合为AVi={AV1,AV2,...,AVm},其中m指第i类训练样本中有m个样本被DCNN识别为第i类。
(2). 使用AVi计算其均值MAVi (Mean Activation Vector), MAVi即是第i类样本的质心。
(3). 使用AVi={AV1,AV2,...,AVm}中的AV1,AV2,...,AVm计算它们到质心MAVi的距离,记距离集合为Di={D1, D2, ..., Dm}
3.1.2 拟合Di中极大值的分布
Di中的极大值分布按照Weibull分类来拟合,此处使用libMR的fit_high()来拟合。
值得注意的是fit_high()和fit_low()的区别,libMR源码说:"Fit_low( ):Use fit_low if your data is such that is smaller is better"。实际上fit_high()和fit_low()的区别就是拟合集合中极大值以及极小值的区别,如果以图1作为数据分布,fit_high()拟合的是右端极大值,fit_low()拟合的是左端极小值。
拟合得到的结果是Weibull分布的累积分布函数CDF。
3.2 矫正得分
3.2.1 得到待预测样本的AV
使用DCNN得到预测样本的AV (即K个已知类得分向量),记为AVx = {Score1, Score2, ..., ScoreK},K指已知类的种类数。
3.2.2 矫正得分
3.1.2步已经得到了每一个已知类的Weibull分布模型,此时需要借助这些模型矫正得分AVx = {Score1, Score2, ..., ScoreK}。
先计算AVx到每一个已知类质心(MAV1, MAV2, ..., MAVK)的距离 {Dx1, Dx2, ..., Dxk}。
假设要矫正AVx中的第j类得分Scorej。将Dxj输入到第j类的Weibull分布模型CDF中输出,此处使用的是mr.w_score(Dxj)。w_score()就是第2节说的CDF,因此mr.w_score(Dxj)返回的是极大值出现在(-∞,Dxj ]中的概率,极大值就是说距离第j类质心很远很远... 极大值在(-∞,Dxj ]中,那么Dxj距离第j类质心更远。样本距离某类质心远意味着样本越不可能输入该类,即mr.w_score(Dxj)返回的是预测样本不属于第j类的概率,那么1-mr.w_score(Dxj)就是样本属于第j类的概率。
以wj=1-mr.w_score(Dxj)作为第j类得分Scorej的修正权值即可。即修正后的第j类得分为Scorej'=Scorej*wj。
其他已知类的得分也是这样矫正。
未知类的得分为Score_unknown=Score1*(1-w1)+Score2*(1-w2)+...+ScoreK*(1-wk)
综上所述,这一步就得到了新的得分向量{Score1', Score2', ..., ScoreK', Score_unknwon}
4. 得分映射为分类概率
将3.2.2节得到的得分{Score1', Score2', ..., ScoreK', Score_unknwon}使用SoftMax映射各分类概率即可。
当最大分类概率在未知类取得或者最大分类概率小于某一阈值,则识别为未知类。