基于MATLAB的离焦模糊图像复原
基于MATLAB的离焦模糊图像复原
摘 要 图像在获取、传输和存储过程中会受到如模糊、失真、噪声等原因的影响,这些原因会使图像的质量下降。因此,我们需要采取一定的方法尽可能地减少或消除图像质量的下降,恢复图像的本来面目,这称为图像复原。通过阅读图像复原技术相关资料,本文主要探讨了维纳(Wiener)滤波、约束最小二乘滤波算法、Lucy-Richardson算法和盲解卷积算法,并使用相关的工具箱函数deconvwnr函数、deconvreg函数、deconvlucy函数、deconvblind函数进行仿真。另外本文对上述算法进行了仿真实现,并分析了四种算法的实验结果。
关键词 图像复原;维纳滤波恢复;约束最小二乘滤波恢复;Lucy-Richardson恢复;盲解卷积恢复
前 言
在实际的日常生活中,人们要接触很多图像,画面。而在景物成像这个过程里可能会出现模糊、失真或混入噪声,最终导致图像质量下降,这种现象称为图像“退化”。因此我们可以采取一些技术手段来尽量减少甚至消除图像质量的下降,还原图像的本来面目,即在预定义的意义上改善给定的图像,这就是图像复原。尽管图像增强和图像复原之间有重叠部分,但前者主要是主观处理,而图像复原大部分是客观处理。复原通过使用退化现象的先验知识试图重建或恢复一副退化的图像。因此,复原技术趋向于将退化模型化并用相反的处理来恢复原图像,即考虑用模糊函数来消除图像的模糊。引起图像模糊有多种多样的原因,举例来说有运动引起的,高斯噪声引起的,斑点噪声引起的,椒盐噪声引起的等等。
本文主要研究离焦模糊图像的复原,离焦模糊图像是指在拍摄时景物与相机的相对运动引起的离焦 ,或是成像区域内不同深度的对象所引起不同程度的离焦 ,还有由于在成像区域中存在不同深度的对象会使自动调焦系统引起混淆而导致拍摄的相片离焦等。因此本文研究使用MATLAB把退化现象模型化,并对几种常用的滤波方法用MATLAB进行了仿真实现,为人们在不同的应用场合及不同的图像数据条件下选择不同的复原算法提供了一定的依据.
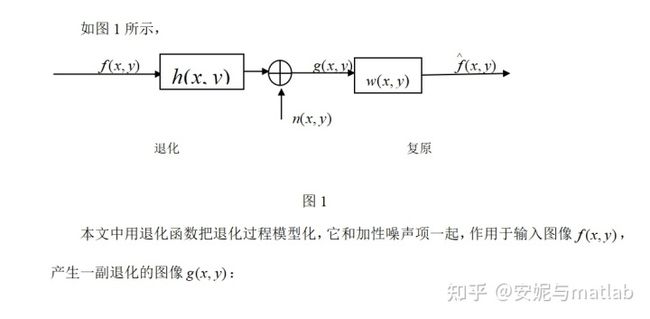
1 图像退化/复原处理的模型
由于退化是线性的,所以空间不变的退化函数可以被模型化为卷积,同样地,复原处理有时也称为反卷积。
2 噪声的特征
图像噪声是图像在摄取或传输时所受的随机信号干扰,是图像中各种妨碍人们对其信息接受的因素。很多时候将图像噪声看成是多维随机过程,因而描述噪声的方法完全可以借用随机过程的描述,即用其概率分布函数和概率密度分布函数。在许多情况下,这些函数很难测定和描述,甚至不能得到,所以常用统计特征来描述噪声,如均值、方差和相关函数等。
3噪声的分类
1、按干扰源分类
图像噪声按照其干扰源可以分为外部噪声和内部噪声。
外部噪声,即指系统外部干扰以电磁波或经电源串进系统内部而引起的噪声。如电气设备,天体放电现象等引起的噪声。
内部噪声:一般又可分为以下四种:
- 由光和电的基本性质所引起的噪声。如电流的产生是由电子或空穴粒子的集合,定向运动所形成。因这些粒子运动的随机性而形成的散粒噪声;导体中自由电子的无规则热运动所形成的热噪声;根据光的粒子性,图像是由光量子所传输,而光量子密度随时间和空间变化所形成的光量子噪声等。
- 电器的机械运动产生的噪声。如各种接头因抖动引起电流变化所产生的噪声;磁头、磁带等抖动或一起的抖动等。
- 器材材料本身引起的噪声。如正片和负片的表面颗粒性和磁带磁盘表面缺陷所产生的噪声。随着材料科学的发展,这些噪声有望不断减少,但在目前来讲,还是不可避免的。
- 系统内部设备电路所引起的噪声。如电源引入的交流噪声;偏转系统和箝位电路所引起的噪声等。
2、按噪声与信号的关系分
乘性嗓声和图像信号是相关的,往往随图像信号的变化而变化,如飞点扫描图像中的嗓声、电视扫描光栅、胶片颗粒造成等,由于载送每一个象素信息的载体的变化而产生的噪声受信息本身调制。在某些情况下,如信号变化很小,噪声也不大。为了分析处理方便,常常将乘性噪声近似认为是加性噪声,而且总是假定信号和噪声是互相统计独立。
3、 按概率密度函数分
这是比较重要的,主要因为引入数学模型,这就有助于运用数学手段去除噪声。
(1)白噪声(White Noise):具有常量的功率谱。白噪声的一个特例是高斯噪声(Gaussian Noise)。在空间域和频域中,由于高斯噪声在数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用在实践中。事实上,这种易处理性非常方便,使高斯模型经常适用于临街情况下。它的直方图曲线服从一维高斯型分布:
(2)椒盐噪声(Pepper Noise):椒盐噪声是由图像传感器,传输信道,解码处理等产生的黑白相间的亮暗点噪声,往往由图像切割引起。椒盐噪声是指两种噪声,一种是盐噪声(salt noise),另一种是胡椒噪声(pepper noise)。盐=白色,椒=黑色。前者是高灰度噪声,后者属于低灰度噪声。一般两种噪声同时出现,呈现在图像上就是黑白杂点。该噪声在图像中较为明显,对图像分割、边缘检测、特征提取等后续处理具有严重的破坏性。
(3)冲击噪声(Impulsive Noise):指一幅图像被个别噪声像素破坏,而且这些噪声像素的亮度与其领域的亮度明显不同。 冲击噪声呈突发状,常由外界因素引起;其噪声幅度可能相当大,无法靠提高信噪比来避免,是传输中的主要差错。
(4)量化噪声(Quatization Noise):是指在量化级别不同时出现的噪声。例如,将图像的亮度级别减少一半的时候会出现伪轮廓。
4直接逆滤波
用于复原一副退化图像的最简单方法是构成一个如下形式的估计:
然后采用的傅里叶逆变换来得到图像的相应估计。这种方法成为逆滤波。由前文中讨论的,模型,我们可以将估计表示为
这个简单的表达式告诉我们,及时准确的知道了,也不能恢复,因为噪声分量是一个随机函数,他的傅里叶变换是未知的。另外,在实际中,有许多为零的情况也是个问题。即使项也可以忽略,用为零的值来除它也将会控制复原估计。
采用逆滤波时,典型的方法是形成比率,然后为了得到逆,将频率的范围限制在接近原点的频率。概念是中的零不太可能在接近原点的地方出现,因为变换的数值通常是该区域中的最高值。
5维纳滤波
维纳滤波(N.Wiener最先在1942年提出的方法)是一种最早也最为人们所熟知的线性图像复原方法。维纳滤波器寻找一个使统计误差函数
我们感兴趣的两个量平均噪声功率和平均图像功率,分别定义为
在这种情况下,即使真实的比率未知,交互式地变化常量并观察复原的结果的实验就变成了一件简单的事。当然,假设函数为常量是一种粗糙的的近似。在前述滤波器方程中,用一个常量数组来代替就产生所谓的参数维纳滤波器。
在IPT中,维纳滤波是使用函数deconvwnr来实现的,函数deconvwnr有三种可能的语法形式。在所有的这些形式中,g代表退化图像,fr是复原图像。第一种语法形式
fr=deconvwnr(g,PSF)
假设信噪比为零。从而,维纳滤波器的这种形式就是前文中的逆滤波器。语法
fr=deconvwnr(g,PSF,NSPR)
假设噪信功率比已知,或是个常量或是个数组;函数接受其中的任何一个。这是用于实现参数维纳滤波器的语法,在这种情况下,NSPR可以是一个交互的标量输入。最后,语法
fr=deconvwnr(g,PSF,NACORR,FAVORR)
假设噪声和未退化图像的自相关函数NACORR和FAVORR是已知的。注意deconvwnr的这种形式使用和的自相关来代替这些函数的功率谱。从相关理论我们可知
其中,“”表示相关操作,表示傅立叶变换。这个表达式说明了对于deconvwnr的使用,通过计算功率谱的傅里叶变换,可以得到自相关函数。噪声的自相关有类似的注释。
若复原图像呈现出由算法中使用的离散傅立叶变换所引入的振铃,则它往往会提醒我们在调用
J=edgetaper(I,PSF)
该函数利用点扩散函数PSF模糊了输入图像I的边缘。这样,输出图像J就是图像I和I的模糊版本的加权和。这个由PSF的自相关函数所决定的加权数组在它的中心区域取J等于I,而在接近边缘的地带等于I的模糊版本。
使用deconvwnr函数复原模糊噪声图像:
f=imread('cameraman.jpg');
LEN=30;
THETA=45;
PSF=fspecial('motion',LEN,THETA);
MF=imfilter(f,PSF,'circular','conv');
wnr=deconvwnr(MF,PSF);
subplot(2,2,1);imshow(f);title('原始图像');
subplot(2,2,2);imshow(MF);title('模糊后的图像');
subplot(2,2,3);imshow(wnr);title('恢复后的图像');
经过仿真,如图所示,我们得到的结果虽然仍有一些噪声存在,但是已经和原图很接近了。因为原图像和噪声函数都是已知的,所以可以正确地估算参量。在实践中,当这些量之一(或更多)未知时,挑战便是在试验中智能地选择所用的函数,知道获得可接受的结果为止。
6 约束的最小二乘方滤波
约束最小二乘滤波恢复函数deconvreg的调用格式:deconvreg(I,PSF,NP,LRANGE,REGOP),其中,I表示输入像,PSF表示点扩散函数,NP、LRANGE( 输入) 和 REGO是可选参数,分别表示图像的噪声强度、拉氏算子的搜索范围和约束算子,同时,该函数也可以在指定的范围内搜索最优的拉氏算子。下面通过程序事例说明约束最小二乘滤波恢复图像:
I=imread ('cameraman.jpg');
PSF=fspecial('gaussian',10,4);
Blurred=imfilter(I,PSF,'conv');
V=.03;
BN=imnoise(Blurred,'gaussian',0,V);
NP=V*prod(size(I));
[reg LAGRA]=deconvreg(BN,PSF,NP);
Edged=edgetaper(BN,PSF);
reg2=deconvreg(Edged,PSF,NP/1.2);
reg3=deconvreg(Edged,PSF,[],LAGRA);
figure
subplot(2,3,1);imshow (I);title('原始图像');
subplot(2,3,2);imshow (BN);title('加入高斯噪声的图像');
subplot(2,3,3);imshow (reg);title('恢复后的图像');
subplot(2,3,4);imshow(reg2);title('振铃抑制图像');
subplot(2,3,5);imshow(reg3);title('拉格朗日算子恢复图像');
图6约束最小二乘恢复对比图
利用振铃抑制恢复图像是几种中恢复效果最好的,其他几种方法也可以恢复但是比较模糊,效果不是很明显。
7 使用Lucy-Richardson算法的迭代非线性复原
Lucy-Richardson(LR)算法假设图像服从Poission 分布,采用最大似然法进行估计,是一种基于贝叶斯分析的迭代算法。其最优估计以最大似然准则作为标准,即要使概率密度函数
大噪声的缺陷。因此,处理噪声项是 LR 算法应用于低信噪比图像复原的关键。
在IPT中,L-R算法是由名为deconvlucy的函数完成的,该函数的语法为
fr=deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT)
其中,fr代表复原的图像,g代表退化的图像,PSF是点扩散函数,NUMIT为迭代次数(默认为10次),DAMPAR和WEIGHT定义如下。
DAMPAR是一个标量,它指定了结果图像与原图像g之间的偏离阈值。当像素偏离原值的范围在DAMPAR之内时,就不用再迭代。这既抑制了这些像素上的噪声,又保存了必要的图像细节。默认值为0(无衰减)。
WEIGHT是一个与g同样大小的数组,它为每一个像素分配一个权重来反映其重量。当用一个指定的PSF来模拟模糊时,WEIGHT
可以从计算像素中剔除那些来自图像边界的像素点,因此,PSF造成的模糊是不同的。若PSF的大小为,则在WEIGHT中用到的零边界的宽度是ceil(n/2)。默认值是同输入图像g同等大小的一个单位数组。若复原图像呈现出由算法中所用的离散傅里叶变换所引入的振铃,则在调用函数deconvlucy之前,要利用函数edgetaper。
下面通过程序事例说明 Lucy-Richardson算法恢复图像:
I=imread('lajiao.jpg');
PSF=fspecial('gaussian',5,5) ;
Blurred=imfilter(I,PSF,'symmetric','conv');
V=.003;
BN=imnoise(Blurred,'gaussian',0,V);
luc=deconvlucy(BN,PSF,5);
figure
subplot(2,2,1);imshow(I);title('原始图像');
subplot(2,2,2);imshow (Blurred);title('模糊后的图像');
subplot(2,2,3);imshow (BN);title('加噪后的图像');
subplot(2,2,4);imshow (luc);title('恢复后的图像');
图7.1 Lucy-Richardson恢复对比图
从图中我们可以看到,经多次迭代,尤其是在低信噪比情况下,重建图像可能会出现一些斑点,这些斑点并不代表图像的真实结构,是输出图像过于逼近噪声所产生的结果。
8 盲去卷积
通常图像恢复方法均在成像系统的点扩展函数PSF已知下进行, 实际上它通常是未知的. 在 PSF未知的情况下, 盲去卷积是实现图像恢复的有效方法。因此,把那些不以PSF知识为基础的图像复原方法统称为盲去卷积算法。
在过去的20年里,一种盲去卷积的方法已经受到了人们的极大重视,它是以最大似然估计(MLE)为基础,即一种用被随机噪声所干扰的量进行估计的最优化策略。简要的说,关于MLE方法的一种解释就是将图像数据看成随机量,它们与另外一族可能的随机量之间有着某种似然性。似然函数用、和来加以表达,然后,问题就变成了寻求最大似然函数。在盲去卷积中,最优化问题规定的约束条件并假定收敛时通过迭代来求解,得到的最大和就是还原的图像和PSF。
工具箱通过函数deconvblind来执行盲去卷积,它有如下语法:
[f,PSFe]=deconvblind(g,INITPSF)
其中,g代表退化函数,INITPSF是点扩散函数的出事估计。PSFe是这个函数最终计算到的估计值,fr是利用估计的PSF复原的图像。 用来去的复原图像的算法是L-R迭代复原算法。PSF估计受其初始推测尺寸的巨大影响,而很少受其值的影响。
若复原图像呈现出由算法中使用的离散傅里叶变换所引入的振铃,则我们在调用函数deconvblind值钱,通常要使用函数edgetaper。下面我们使用函数deconvblind估计PSF:
I=imread('lajiao'.jpg');
PSF=fspecial('motion',10,30);
Blurred=imfilter(I,PSF,'circ','conv') ;
INITPSF=ones(size(PSF));
[J P]=deconvblind (Blurred,INITPSF,20);
figure
subplot(2,2,1);imshow (I);title('原始图像');
subplot(2,2,2);imshow (Blurred);title('模糊后的图像')
subplot(2,2,3);imshow (J);title('初步恢复后的图像');
该算法优点是,同时恢复了图像和点扩张函数,在对失真情况毫无先验知识的情况下, 仍能实现对模糊图像的恢复操作。利用 MATLAB实现的图像恢复, 并对恢复图像的失真情况做了改善。在进行图像恢复时,重建 PSF,对图像进行重建, 得到恢复的图像。
总 结
本文介绍了图像退化的原因并且简要介绍了当前主流的图像复原方法,并通过对各种复原方法的仿真,了解了各种方法的优劣性,为我们在实际生活提供依据。但是无论是哪一种方法都有所局限性,我们应该努力致力于研究新型的优秀的图像复原方法,来获得更好的图像复原效果。同时,我们知道算法利用的信息越多信息的准确性越高,则复原图像的质量就越高。而且采用 MATLAB实现图像恢复,通过几条简单的MATLAB命令就可完成一大串高级计算机语言才能完成的任务,简捷明快。大多数图像处理模型是可以通过使用MATLAB的基本函数通过编程实现的。
参考文献
[1]张燕妮.离焦模糊复原方法研究[D].大连:大连理工大学,2005
[2]徐飞.施晓红. MATLAB应用图像处理[M].西安电子科技大学出版社,2002.
[3]路敬袜,王冬梅. 基于MATLAB的图像复原算法的研究[D].硕士学位论文.
[4]阮秋琦等译. 数字图像处理(MATLAB版)[M].北京:电子工业出版社,2005.
[5]张德丰,张葡青.维纳滤波图像恢复的理论分析与实现[J].中山大学学 报,2006,45(6)44-47.
[6]14曹茂永,孙农亮,郁道银.离焦模糊图像清晰度评价函数的研究[J].仪器仪表学报,2007,
22(3):259-268.
[7]章毓晋.图像处理和分析[M].北京:清华大学出版社,1999.
[8]苏开亮.运动模糊图像的恢复及恢复质量评价[D].西安:西安电子科技大学出版社,2010,21-25.
[9]龚声蓉,刘纯平,王强. 数字图像处理与分析[M],清华大学出版社.2006.
[10]Edmund Y L. Digital restoration of defocus image in the wavelet domain[J].Applied Optics.2002,141(126):4806-4811.
[11]Tnoa Zznia.Blur identification analysis in blind image deconvolution using Markov random fields[J]
.Pattern Recognition and Image Analysis,2001,11(4):699-700.
[12]Williamk,Faramarzd.Fast computational techniques for Pseudoinverse and Wiener image restoration [J].IEEE Trans on computer,1997,26(6)571-580.