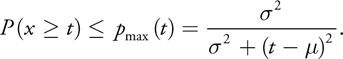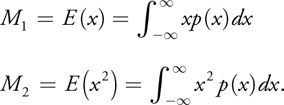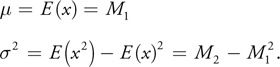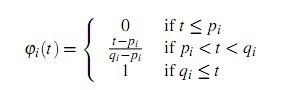Layered-->Variance-->Shadow Map

 

    好吧，在被这个算法折腾了许多天之后，我终于对它竖起了中指。这几天的经历让我明白了一个道理：对于数学基础不好的人来说，对待图形学最好远观不可亵玩焉；如果坚持硬闯却又碰巧E文不咋地，那受罪程度真叫人生不如死。最后，看待算法最好别太坚持“追求极致”，如果付出了太多而收获了太少，那么采取一种“妥协”的态度也未尝不可。anyway，LVSM算法我没有全部弄明白，但也不是没有收获。虽然目前这种半瓶子醋的状态让我尴尬，但除了适可而止，我还能怎么样呢。毕竟，智商就这么点~

Shadow Map

    基于硬件的动态阴影一般有两种技术，Shadow Volume和Shadow Map。 不过SV已经处于被淘汰的境地，加上算法复杂，和occluder复杂程度有直接关系，因此已不是主流；SM(呃，这名字)算法简单，和场景复杂度无关，唯一的成本就是两遍pass渲染。刚才说这两种算法都是基于硬件（Hardware）的，针对SM来说的话就是需要“深度模板缓存（DSB, Depth-Stencil Buffer）”以及“渲染到纹理”（RTT, Render To Targets）”的硬件支持。不过，无论是GL还是DX，对这两项的支持通常都不是问题。此外如果硬件支持可编程管线（programmable pipeline）的话更好。因此学习阴影的话建议还是选择SM。

算法思想

    鉴于SM的介绍网上有成堆的资料，因此看不明白的可以找其他读物阅读。SM进行两遍pass渲染，第一遍pass站在灯光（light）的角度对场景进行渲染，此时打开z-buffer，并RTT到自己创建的一张纹理中，此时纹理中的像素代表的是，以light的角度看过去，相应位置距离light最近的深度，注意这里你要辩证地看，这也同时表示从light中射出的光最远只能打到这个位置了（再往后的就被这个像素遮挡了）。而这张纹理图就是shadow map；第二遍pass站在视点角度再次对场景渲染，并在光栅化阶段时，对每一个要处理的像素，坐标变换到light坐标系中，并与对应的shadow map中的像素比大小：如果current pixel > shadowmap pixel，说明该像素被挡住了，因此判断这个像素处于阴影中，应该将此像素涂黑；否则，表示它处于光照中，接下来计算它的光照值。对所有的像素进行如此操作，就完成了阴影的绘制。

缺点

    SM虽然不错，但远非完美。

    1）由于它的阴影算法是“像素级”的，因此不免在阴影边缘留下“锯齿化”的走样痕迹；
    2）这是一种硬阴影，没有“半影”（penumbra），从黑到白，从0到1，中间没有自然过渡，导致不真实；
    3）对灯光类型有限制，一般要求聚光灯，最起码也是方向光，对于点光源无奈。因为点光源按此原理的话要多个RTT（一般是6个,组成一个cube，灯光置于中心）,开销太大。
    4）对于第二遍pass处理像素阶段，变换到light空间的pixel不可能和shadowmap中的像素值精确匹配，导致z-fighting问题（关于z-fighting，看这里。注意要FQ，因为wiki的图片为伟大地墙在外面了。可如果不看图，又没法直观领悟到那是什么）。

    因此，围绕这些问题，业界牛牛们都提出了许多行之有效的解决办法。其中1），2）是重点，讨论的也最多，因此放到下面说；3）的话貌似没有什么办法，这是SM算法本质决定的，如果坚决用点光源，就做好成本花费的准备；4）的问题可以加一个z-偏移量来解决。

PCF(Percentage Closer-Filter)

    1），2）这二者问题的本质是相同的。解决办法是“模糊像素”，PCF（Percentage Closer-Filter）就是这样一种技术，它的本质是线性滤波，比如对2*2像素三线性滤波，那么其结果就是4个初始结果的带权均值，比如0.25或者0.5或者0.75这样。这种办法也是对付锯齿化走样的常规方案。通过滤波就能产生过渡颜色，同时也起到模糊锯齿的作用。

    但PCF也有缺点。第一，它所产生的软阴影（soft shadow）是伪软阴影，因为它的“半影”是通过模糊边缘来模拟，不是真正计算出来的，这样无论灯光离物体有多远、光源面积有多大，它产生的半影范围永远都是固定的，这有悖真实；第二，滤波时需要对相邻像素采样，采样本身又是一个费时费力的过程。因此采样的区域越大，虽然其效果越好，但成本越高，效率越低。

    有人说对纹理的采样滤波是通过硬件执行的，速度很快，因此不会出现上面描述的“效率低下”——没错，如果我们打算直接对这张shadow map滤波的话，那效率的确不是问题。但单纯地滤波shadow map没有意义，滤波之后的均值还是depth，而只靠depth我们是无法产生阴影的。阴影的产生取决于“比较”：shadow map中像素代表的depth值，与我们考察的对应当前像素的depth值之间的比较。如果我们拿滤波后的depth去比，其结果还是非0即1，非黑即白，因此产生不了过渡的阴影。

    那PCF的“滤波”是怎么做到的呢？它是先作比较，产生出4个（2*2像素）0、1结果，然后再对这4个0、1结果进行平均，得到一个介于0到1之间的值。这意味着，每滤波一个像素，都要手动采样4次并比较4次才能得到结果。这就是PCF的代价所在，毕竟手动计算和硬件处理在效率上可不是同日而语的。

    PCF的效率影响了它的使用效果。对此，有另外一种思路可以达到同样甚至更好的效果，并且还可以直接滤波shadow map（意味着支持硬件），效率大幅提升。这就是Variance Shadow Map 。

 

Variance Shadow Map

   Variance在这里为“方差”之意。 VSM算法的背后用到了一个概率学原理：切比雪夫不等式（Chebyshev’s Inequality）。CI大意是说，在一个分布未知的样本中，如果知道了该样本的期望E与方差D，那么就可以估计出样本分布在某一区间的概率上限。教科书中常见的描述是双端的形式，即表示样本的“绝对值”大于（或小于）某值的概率；而这里用到的是单端形式（one-tiled），考察的是样本本身。它的公式描述如下：

    其中μ代表期望，σ代表方差，t代表一个指定的样本值，p代表概率。这个公式表明，在分布未知的情况下，样本中所有随机变量大于等于某一样本值t的概率有一个上限，就是pmax(t)，它由样本的期望、方差与t来决定。

    另外，还需要介绍下期望与方差的求算。下面的图可以简单说明这一切：

 

 

 

    M1、M2表示“矩”（Moment）。这又是一个概率学概念，可以把数学期望μ看作一阶矩，把方差σ看作二阶钜。   

算法思想

    VSM与标准的SM基本是类同的：都分两遍pass渲染，并且每一遍的渲染目的都一样。唯一不同的是，在第一遍pass中，存储在Shadow Map中的是一个深度值（z-depth），而在Variance Shadow Map中，存储的是两个分量（two components）: 深度值与深度值的平方。这可以借助占用像素的两个通道来办到（比如R通道放深度值，G通道放深度值的平方）。接下来，就触及到该算法的核心：完成第一遍pass后，对VSM进行每单位区域（比如，仍然是2*2为一个range）的硬件线性滤波。滤波后每像素存储的两个分量，其意义就发生了微妙的变化：第一个分量表示该range内所有像素深度值的均值，也可以看作对应的期望，即上面的M1；而第二个分量表示该range内所有像素值的平方的期望，即上面的M2。依据M1和M2我们就可以求出该range的μ和σ。按照切比雪夫不等式，我们就可以估计出这片range内其深度值大于某一值t的概率上限。

    第一遍pass中，我们逐一计算M1和M2并存储到VSM中，然后对这张VSM进行范围为range的硬件线性滤波；第二遍pass中，我们依然用视点角度渲染场景，对光栅化的每一像素，计算它在灯光坐标系中的深度值，并把这个值设为t；调取VSM中对应位置的像素，利用M1和M2计算出μ和σ，先判断t与μ的大小关系：如果t<=μ，则表示当前像素的深度小于等于range的深度均值，则判断它没有被遮挡；否则，判断它被遮挡，这时利用切比雪夫不等式计算出pmax(t)，该值表示range内深度值大于等于t的像素个数的概率上限，这个概率可以看作比率。该比率表示光照射到当前像素的光线数量（比t小的像素表示它遮挡住了当前像素，也就是说光线没有射到该像素上；相反，则就表示射到了t上），因此，这个比率就相当于光照强度，这是一个介于0到1之间的过渡数值。用它乘以黑色，就是最后实际的阴影值。注意，我们的算法是用上限值pmax(t)近似模拟了实际比率p(t)，但其实pmax(t) > p(t)，只不过二者相差不大。但这个误差依然会导致一些问题，会放到下面讨论。

 

优点

    VSM的实际效果好于等于进行了PCF的SM。相比单纯的SM，它实现了软边缘以及消除了锯齿；相比PCF，它的效率大大提升，实际上这是它的主要优势。上面我们提及，PCF因为无法直接利用硬件滤波SM，而不得不手动采样滤波“比较”结果来产生0与1 。 但VSM却没有此劣势，它可以直接硬件滤波，利用滤波产生了区域深度值的一阶矩与二阶矩，再由此计算出期望和方差，进而得到比率上限值。可以说，正是利用了切比雪夫不等式，使得硬件滤波派上了用场，从而大大提升了效率，同时效果又非常好。这真的是一个相当棒的设计。

Light Bleeding

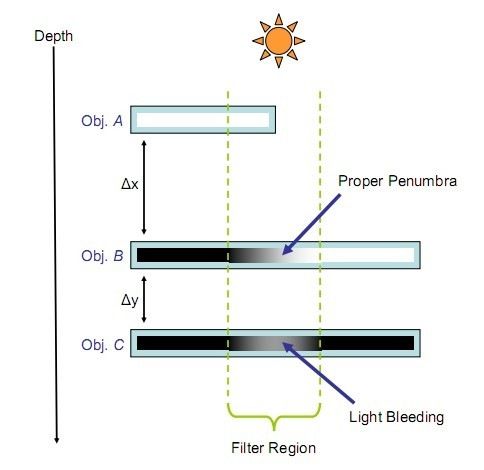
    光渗现象（light bleeding）是VSM最臭名昭著的一个缺点。虽然它不一定会在你的场景中发生，但是，它的确有发生的危险，尤其是在深度复杂度较高的场景中。按我的理解，深度复杂度应该是指场景中互相遮挡的occluder比较多时的情况。下面一幅图说明了这一点。

 

 

    obj.c被obj.b完全遮挡住了，但你可以看到在obj.c的filter region内，有一段较亮的区域，这本是不该被照亮的地方，这便是light bleeding。你可以发现obj.b的效果完全是正确的，但倘若它下面还有东西，比如这里的obj.c，那么在下层就有可能发生光渗，尤其是Δy远远大于Δx的时候。发生这种现象并不是碰巧哪里出错了，这是由切比雪夫不等式的本质决定的：它只估算出概率发生的上限，而不是准确值。换句话说得出的值永远是偏大的。你可以观察pmax(t)的公式，你会发现无论pmax(t)有多小，只要方差σ不为零，这个值就永远不为零，这样light bleeding就无法避免了。下面是一张发生light bleeding的实际效果图：

 

光通过板凳“渗”到了地上，形成了一些怪异的光圈

    我查了一些资料，在VSM的基础上解决light bleeding的办法并不是很多。Gpu Gems3提供了一种“减轻”的方法：即当比率小到一定程度时，干脆将其设为0 。 但这并不能消除lb，而且如果条件越苛刻，它所创造的半影也越暗。另外还有一种Exponential VSM技术，不过它是大作ShaderX6其中一篇文献，至今没找到免费阅读的合理途径。在这里介绍的是另一种经典的方法：Layered VSM 。

 

Layered Variance Shadow Map

    顾名思义，LVSM是对VSM的分层（layered），每一层存储一张VSM，以达到对深度值的“分辖”控制。在每一层中，都有一个包装函数（wrapped function），对原始的深度值进行包装，所谓“包装”，其实就是对深度值进行分段，判断它属于哪一层管辖的深度，然后进行该层VSM的求算。典型的包装函数如下：

 

　　　

    其中，pi,qi是第i层的边界，t是具体的深度值，φi(t)是包装后的值。可以看到，这样一个函数把每一层的深度都卡（clamp）在了[0,1]之间，并把该深度重新缩放在相对于该层的考量空间中。例如，对0到1的全局深度空间划分为5层：[0, 0.22]， [0.2, 0.42]， [0.4, 0.62]， [0.6, 0.82]， [0.82 1]。可以看到每层之间都有一定的重叠，这是为了处理好层与层之间的边际问题。在第一遍pass中，我们用5个VSM来渲染它们。渲染每一个像素时，对该像素的深度进行“包装”（根据上面的公式），这实际上就把该像素“派发”到管辖它的层（layer）中。第二遍pass中，我们依然站在视点角度再次渲染场景，对待光栅化的像素，判断它在灯光坐标系中的深度，然后找到对应的layer，然后只用该层layer的VSM来计算它的阴影，其处理手法与标准的VSM中处理手法一致。这种办法可以大大减弱light bleeding问题，甚至完全消除。而且layer设置的越多，效果也越明显，当然。代价也相应也越大。

    LVSM的本质是有效降低了方差σ。我们知道，“方差”表示样本单体与样本期望的偏离程度，方差越大，表示偏离越大，而偏离越大，发生light bleeding的机率也越大（看pmax(t)公式的分子）。所以可以用方差来反映发生lb的机率。通过分层，“偏离”的程度被大大降低（两个彼此之间偏离过大的像素深度被分到了两个不同的层layer，彼此之间毫无影响），因此方差减小了许多，从而有效降低了lb的发生。

Multiple Render Targets

    现在我们讨论一下如何把深度值渲染到多个VSM中。这用到了需要硬件支持的技术：多渲染目标（MRT，Multiple Render Targets)。MRT和RTT是一样的，只不过RTT是渲染场景到一个纹理目标中，而MRT则要把相同的场景渲染到多个不同的纹理目标中去。该概念的介绍见这里。这里的算法中，有多少个layer,就有多少个render target，每一层layer占用一个render target。至于硬件支持render target最大的数目，以及甚至说支不支持MRT，取决于你购买的显卡的能力，在使用前需要检查。注意这和早先说过的处理点光源的做法还不一样：处理点光源时，我们需要多个不同角度的RTT，每一个RTT都要重新计算所有的坐标变换，每一个RTT都要利用一遍pass；而这里的处理做法，是把同一个角度（即站在有向灯光的角度）看到的场景渲染到不同的纹理目标中，只需要一遍坐标变换，而且这一切都发生在同一个pass中。这可以获得硬件加速的支持。因此MRT具有很高的效率。

Weighted K-MEANS Algorithm

    还要讨论下如何分层。实际上这是LVSM算法中的关键：如何智能地分层，能够使“消除light bleeding”效果最大化？

    这里用到了一种聚类（cluster）算法，据我所知“聚类”是“数据挖掘”领域内的一个概念，但我并不熟悉它，因此只能临时抱佛脚。关于聚类的介绍建议看这里。这里用到一种典型的聚类算法：带权k-means 算法（Weighted K-MEANS Algorithm）。详细的介绍我无法提供，自己去找吧。但可以解释一下用在这里的理论基础：当我们渲染一张SM时，我们实际上是存储了一个分布在一维空间的深度集合。比如对于一张512*512的shadow map，那么就有512*512个深度值坐落在[0,1]这个空间中。它们是怎么分布的？我们当然无从得知，但它们当然也不会平均分布。我们虽然不知它们的分布状态，但我们可以想见，它们一定是按“一堆一堆”的形式聚集在一起的，比如以0.2为中心有一个聚落，又以0.75为中心有一个聚落，等等如此。为什么？因为这张shadow map映射的一个场景的形象，而这个场景中每一个“表面”必然是平滑连续过渡的，然而当前景和背景相离较远时，就会出现一个断层，反应在深度上就是一个突然的跳跃（比如从0.2突然跳到了0.75），从而产生了另外一个中心点。既然这个集合符合这样的规律，那就一定可以为这些值按深度的聚落中心归类，从而找出这些断层的大概位置，这就是使用“聚类”算法，使用k-means算法的原因。

    然而，关于此的具体过程欠奉。因为我脑子里一直搞不清一个问题：如何对于一张VSM在不手动采样的前提下遍历深度数据的？ 不遍历，没法找聚落中心；遍历，由于是手动采样，效率又会大打折扣。况且，这个paper竟然说这里用的是迭代法（iterate）。作者没有提供任何代码以及伪码，所以我在浆糊的脑子里转了几圈，最终放弃了对它的研究。

    我自己的一个简单设想是，其实在最初计算VSM时，就找到map中一个最小深度值min和最大深度值max，然后对此[min,max]区间进行平均分层，虽然这个办法的确不够智能，但我想，足够了。通过下图可以推测出，用这样一个“不智能”的土法子，当layer数为6时，效果还不错。

 

 
看，Uniform LVSM-6(94fps)，虽然效果略差，但比同级的Lloyed LVSM-6(73fps)效率要高，还是赚了 =.=!

 

 

Next

    接下来，我就要尽快抓紧对此的实现了。
   
    飞舞吧，山都满坡！

 

Reference

１．gpu gems3 : Chapter 8. Summed-Area Variance Shadow Maps
２.  http://www.punkuser.net/lvsm/