用一条曲线遍历整个平面 浅析 Hilbert 曲线及其变种在 Turtle 上的设计与实现

本文主要介绍如何用多重递归的方法以 Turtle 实现 Hilbert 分形曲线的画法。首先给出基本的绘图函数：

void Turtle::forward(Turtle turtle, int sideLength); // turtle 从当前位置前进 sideLength 距离并绘制
void Turtle::turn(Turtle turtle, double angle); // turtle 从当前方向顺时针旋转 angle 度

正方形迭代

先从基本的 Hilbert 曲线开始说明。对于任一阶数为 order 的 Hilbert 曲线，都可以将其分为四个阶数为 order - 1 的 Hilbert 曲线和三条用于连接它们的线段；当阶数为 0 时 Hilbert 曲线退化成点，故阶数为 1 时 Hilbert 曲线只有三条线段。

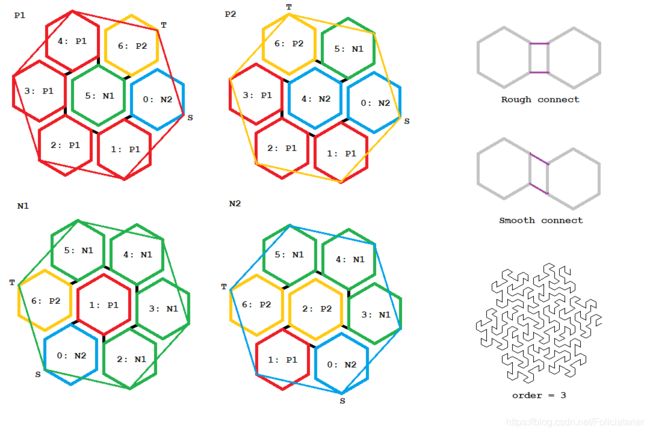
将任一阶数的 Hilbert 曲线都抽象成一个正方形，忽略其内部细节，只保留曲线的入口 S 和出口 T，则可发现，任一阶数为 order 的 Hilbert 曲线都只存在 2 种，分别记为 P 和 N，其中 P 曲线的出口 T 在入口 S 逆时针方向的邻点上，而 N 曲线的出口 T 在入口 S 顺时针方向的邻点上。

为了实现方便，先约定一些绘制任一阶数 Hilbert 曲线的规则，例如 turtle 朝向在程序开始前和结束后必须保持一致。还要约定 P 曲线和 N 曲线的标准绘制样式，在这里约定当程序开始前 turtle 朝向正上方时，P 曲线和 N 曲线的出口 T 一定在入口 S 的正上方。具体实现细节见以下代码：

	private static void FractalTetPosi(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		turtle.turn(270);
		FractalTetNega(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(90);
		FractalTetPosi(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		FractalTetPosi(turtle, order - 1, sideLength);
		turtle.turn(90);
		turtle.forward(sideLength);
		FractalTetNega(turtle, order - 1, sideLength);
		turtle.turn(270);
	}
	private static void FractalTetNega(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		turtle.turn(90);
		FractalTetPosi(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(270);
		FractalTetNega(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		FractalTetNega(turtle, order - 1, sideLength);
		turtle.turn(270);
		turtle.forward(sideLength);
		FractalTetPosi(turtle, order - 1, sideLength);
		turtle.turn(90);
	}

正六边形迭代

接下来考虑 Hilbert 曲线的变种，如何以正六边形的迭代方法遍历整个平面。整个设计过程与上文不同的是，我们并不知道最终结果的分形曲线的具体样式，所以只能根据 Hilbert 曲线的设计过程类比实现。

由类比可得，任意阶数为 order 的新分形曲线，都可将其分为七个阶数为 order - 1 的新分形曲线和六条用于连接它们的线段。这时就要问了，为什么是七个？或者之前就该问，为什么 Hilbert 曲线是分成四个？一种解释是一个大正方形可以分为四个小正方形，但这样新分形曲线就无法设计了，因为不管怎样一个大的正六边形都无法分成若干个小的正六边形。其实无论是两个小正方形拼成的长方形，还是三个小正方形拼成的 L 形，都能铺满整个平面，为什么非得是四个不可呢？笔者在这里的理解是，Hilbert 曲线分成四个的原因之一是保持其 90 度旋转对称性（Peano 曲线分成九个同理），新分形曲线分成七个是为了保持其 60 度旋转对称性。七个正六边形拼成的图形虽然不是六边形，但新图形仍然可以铺满整个平面；七个新图形拼成的图形离六边形更远了，但仍然可以铺满整个平面，而且这些图形都是 60 度旋转对称的。而只要是 60 度旋转对称的可铺满平面的图形，我们都可以将其抽象成正六边形。

接着是标准绘制样式的设计。对于 Hilbert 曲线，这其实没得选，因为在四个小正方形拼成的大正方形中，只能从一个小正方形走到与其边相邻的另一个小正方形的哈密顿路径都可以等价成一种，即 U 形路径，在设计时无非正着走和反着走两种，所以只有 P 曲线和 N 曲线。但在七个小的正六边形拼成的大图形中，仍然是求只能从一个小的正六边形走到与其边相邻的另一个小的正六边形的哈密顿路径，这路径就比较多了。显然开始或结束点在中间的小的正六边形的路径是不可取的，而抽象后我们只关心入口 S 和出口 T 的相对位置，所以等价后只有 3 种，分别是出口 T 在入口 S 的邻点上，邻点的邻点上和对点上。由于还要分正着走和反着走，则分为 5 种标准绘制样式，分别为出口 T 在入口 S 逆时针方向的邻点上，记为 P1；出口 T 在入口 S 顺时针方向的邻点上，记为 N1；出口 T 在入口 S 逆时针方向的第二个点上，记为 P2；出口 T 在入口 S 顺时针方向的第二个点上，记为 N2；出口 T 在入口 S 的对点上，记为 Z（Z 无论正着走还是反着走，入口 S 和出口 T 的相对位置都是一样的）。在实际实现中，没有实现 Z 曲线（因为没用上）。

然后是衔接七个小的正六边形的线段的实现。对于 Hilbert 曲线，这部分其实非常自然；但对基于六边形的新分形曲线，要想做到如 Hilbert 曲线般自然，则还需费一番功夫。如何才能称衔接线段自然？我们希望其长度等于一阶曲线每条线段的长度，而且其方向在一阶曲线的线段中有迹可循。于是，一些看似对齐的设计需要修改成看起来不那么对齐的样子，才能让衔接显得足够自然。

最后是一个容易被忽视的问题，即入口 S 和出口 T 的位置。对于 Hilbert 曲线确定位置非常显然，但对于新分形曲线，由于 order > 1 时并非正六边形，故易定错位置。在确定 S 后，T 的位置一定和在整个图形旋转若干个 60 度后 S 的位置重合，并且 S 一定要取最外层的点，才能确保抽象后的正六边形面积等于实际图形的面积。具体实现细节见以下代码：

	private static void FractalHexPosi1(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		turtle.turn(300);
		FractalHexNega2(turtle, order - 1, sideLength);
		turtle.turn(300);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(120);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.turn(300);
		turtle.forward(sideLength);
		FractalHexPosi2(turtle, order - 1, sideLength);
		turtle.turn(300);
	}
	private static void FractalHexNega1(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		turtle.turn(60);
		FractalHexNega2(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(60);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		turtle.turn(240);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(60);
		FractalHexPosi2(turtle, order - 1, sideLength);
		turtle.turn(60);
	}
	private static void FractalHexPosi2(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		turtle.turn(300);
		FractalHexNega2(turtle, order - 1, sideLength);
		turtle.turn(300);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(60);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(120);
		turtle.forward(sideLength);
		FractalHexNega2(turtle, order - 1, sideLength);
		turtle.turn(300);
		turtle.forward(sideLength);
		turtle.turn(240);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(60);
		FractalHexPosi2(turtle, order - 1, sideLength);
	}
	private static void FractalHexNega2(Turtle turtle, int order, int sideLength)
	{
		if(order <= 0)
			return;
		FractalHexNega2(turtle, order - 1, sideLength);
		turtle.turn(300);
		turtle.forward(sideLength);
		FractalHexPosi1(turtle, order - 1, sideLength);
		turtle.turn(120);
		turtle.forward(sideLength);
		turtle.turn(60);
		FractalHexPosi2(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(240);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(300);
		FractalHexNega1(turtle, order - 1, sideLength);
		turtle.forward(sideLength);
		turtle.turn(60);
		FractalHexPosi2(turtle, order - 1, sideLength);
		turtle.turn(60);
	}

正三角形迭代及其它

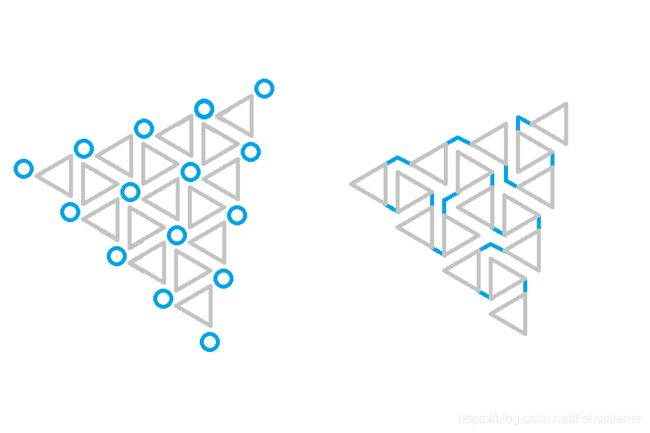
那么，是否存在以正三角形的迭代方法遍历整个平面的曲线呢？初看上去似乎可行，但实际设计时，会发现无论是四个还是九个小正三角形拼成的大三角形，都不存在哈密顿路径遍历所有边相邻的小正三角形，详细来说，即对于处于大正三角形角上的小正三角形，只有一个小正三角形与其相邻，而这样的小正三角形有三个，故不存在哈密顿路径。而且，在进行衔接时，六个小正三角形中间会形成空穴，平均一个小三角形会形成 1/2 个空穴。通过巧妙安排路径通过空穴，可以解决哈密顿路径的问题，但这种设计使得绘制样式失去了 120 度旋转对称性，必然需要更多的等价标准样式来实现。还有一种设计思路是通过三个小的正六边形拼成的图形设计，这样可以保持 120 度旋转对称性，这里不再赘述。由于正三角形和正六边形在平面上的对偶性，实现结果和上文也许殊途同归。

非正多边形又是否可以设计分形曲线？理论上可以，但很难找到一种简单的实现方法。分形曲线一大特性是构造简单，失去构造简洁性的分形曲线是否已失去其初衷？再者，对应 Hilbert 曲线的高维形式，以正四面体或正八面体的迭代方法遍历整个空间的曲线又是否存在？这些问题仍然值得思考。