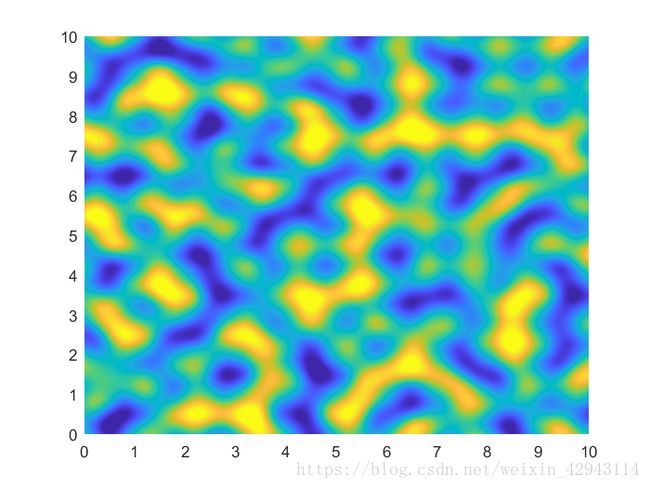
柏林噪声（Perlin Noise）的matlab实现

柏林噪声（Perlin Noise）的matlab实现

柏林噪声是1983年Ken Perlin提出的噪声，用于模拟自然纹理，比如水波，手绘，火焰，大理石等纹路，也可以生成残蚀效果动态烟雾等各种常见特效。

根据计算机噪声产生的方法，可以分为梯度噪声和数值噪声，而柏林噪声就是梯度噪声最典型的代表之一。其中本文的算法和思路都来自于下面这篇博客，有兴趣的可以认真看一看这篇博客的内容。
【图形学】谈谈噪声

下面介绍一下一维、二维以及更高维度下柏林噪声（Perlin Noise）的matlab实现。

1.二维柏林噪声

二维柏林噪声是柏林噪声的基础，理解了二维柏林噪声之后有助于更快的实现其它维度的噪声。

算法的思路如下：

生成晶格点矩形网格
生成计算点网格，计算点网格范围要小于晶格点网格，而且要比晶格点网格更密。
给晶格点网格的格点生成随机单位圆梯度
分别计算每个计算点的数值：
	确定计算点在在晶格中的位置，寻找该点所在的矩形网格的4个角点（晶格点）
	分别计算每个角点对该计算点的影响：
		计算该点与角点之间的方向向量
		用方向向量与角点（晶格点）的梯度向量做点积
	对四个点进行加权，得到该计算点的数值，使得数值在区域内平缓过渡
绘制噪声图谱

接下来用图片来介绍一下算法的实现思路：

分别计算4个角点对该点的梯度影响：


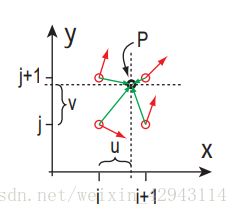
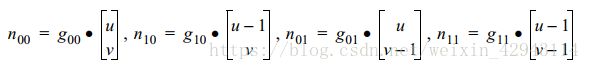
实际计算中，取整数点作为晶格点，用来生成各个梯度向量。其中u,v代表计算点的小数点部分，即x-floor(x)和y-floor(y)。之后用方向向量分别和对应的四个角点的梯度值做点积，生成n00, n10,n01和n11。n00代表和矩形左下角↙的梯度点的点积，n10代表右下角↘的点积，n01代表和左上角↖的点积，n11代表和右上角↗的点积。g代表各对应角点的梯度向量。

之后四个值加权处理。加权采用先x加权，后y加权。即先利用n00和n10加权为n0，再利用n01和n11加权为n1，这一步是x加权；之后再利用n0和n1加权为n，这一步是y加权。加权公式为：
$$n_0=n_{00}(1-f(u))+n_{10}f(u)$$
$$n_1=n_{01}(1-f(u))+n_{11}f(u)$$
$$n=n_0(1-f(u))+n_{1}f(u)$$
一般$f(u)$取$f(0)=0，f(0.5)=0.5，f(1)=1$的函数，低阶的可以取$f(u)=u$，高阶的可以取：
$f(u)=3u^2-2u^3$或者$f(u)=6u^5-15u^4+10u^3$，阶数越高图像平滑度越好，但是计算量越大。

接下来附上matlab代码

function zmat=perlinnoise2f(limx,limy,dx,dy)
%先定义变长大小，以及精度，以整数点为参考点。默认最小点为0。
% limx=[0 10];
% limy=[0 10];
% dx=1/16;
% dy=1/16;
% 公式的引用格式：zmat=perlinnoise2f([0 10],[0 10],1/16,1/16);
%第一步
%定义网格，以及各随机向量矩阵
minx=limx(1);maxx=limx(2);
miny=limy(1);maxy=limy(2);
numx=maxx-minx+1;
numy=maxy-miny+1;
numx_z=(maxx-minx)/dx+1;
numy_z=(maxy-miny)/dy+1;

[uxmat,uymat]=randxymat(numx+1,numy+1);%生成随机向量阵，注意边缘所以多了一行一列。参见后面的公式randxymat
zmat=zeros(numy_z,numx_z);%生成计算点网格，预设随机云图

j=0;
for x=minx:dx:maxx
    j=j+1;%x坐标索引
    k=0;
    for y=miny:dy:maxy
        k=k+1;%y坐标索引
        %n00计算
        ddx=x-floor(x);
        ddy=y-floor(y);
        ux=uxmat(floor(y)-miny+1,floor(x)-minx+1);
        uy=uymat(floor(y)-miny+1,floor(x)-minx+1);
        n00=GridGradient(ux,uy,ddx,ddy);%参见后面的公式GridGradient
        %n10计算
        ddx=x-floor(x)-1;
        ddy=y-floor(y);
        ux=uxmat(floor(y)-miny+1,floor(x)-minx+2);%注意边缘点数据关联问题，这就是前面多了一行一列的原因
        uy=uymat(floor(y)-miny+1,floor(x)-minx+2);
        n10=GridGradient(ux,uy,ddx,ddy);
        %n01计算
        ddx=x-floor(x);
        ddy=y-floor(y)-1;
        ux=uxmat(floor(y)-miny+2,floor(x)-minx+1);
        uy=uymat(floor(y)-miny+2,floor(x)-minx+1);
        n01=GridGradient(ux,uy,ddx,ddy);
        %u11计算
        ddx=x-floor(x)-1;
        ddy=y-floor(y)-1;
        ux=uxmat(floor(y)-miny+2,floor(x)-minx+2);
        uy=uymat(floor(y)-miny+2,floor(x)-minx+2);
        n11=GridGradient(ux,uy,ddx,ddy);
        %然后再加权
        n0=lerp(n00,n10,x-floor(x));%参见后面的
        n1=lerp(n01,n11,x-floor(x));
        zmat(k,j)=lerp(n0,n1,y-floor(y));%把最终数据n存储到相应的矩阵中
    end
end
%把最终数值规划到0，1之间
zmat=zmat+0.5;
zmat(zmat>1)=1;zmat(zmat<0)=0;

% 生成图像
% [xmat,ymat]=meshgrid(minx:dx:maxx,miny:dy:maxy);
% figure
% pcolor(xmat,ymat,zmat)
% shading interp

end

function u=GridGradient(ux,uy,dx,dy)%数组相乘，其实就是点积，也可以用dot()函数替换
    u=ux*dx+uy*dy;
end

function u=lerp(a,b,t)%权重相加
    tw=6*t.^5-15*t.^4+10*t.^3;%6*t.^5-15*t.^4+10*t.^3;%3*t.^2-2*t.^3;%
    u=(1-tw)*a + tw*b;
end

function [uxmat,uymat]=randxymat(numx,numy)%单位圆内随机向量
    num=numx*numy;
    uxmat=zeros(numy,numx);
    uymat=zeros(numy,numx);
    %采用不断生成随机向量，然后检测是否在单位圆内的方法。这个方法维度越高效率越低。
    for j=1:num
        k=0;
        while k==0
            randxy=rand(1,2);
            if (randxy(1)-0.5)^2+(randxy(2)-0.5)^2<=0.25
                k=k+1;
                uxmat(j)=randxy(1);
                uymat(j)=randxy(2);
            end
        end
    end
    uxmat=(uxmat-0.5)*2;%把随机向量调整为[-1,1]之间，这样生成的图像好看。
    uymat=(uymat-0.5)*2;
end

上述函数引用的方法为：

limx=[0 10];
limy=[0 10];
dx=1/16;
dy=1/16;
zmat=perlinnoise2f(limx,limy,dx,dy);
figure
[xmat,ymat]=meshgrid(0:dx:limx(2),0:dy:limy(2));%划分网格
pcolor(xmat,ymat,zmat)
shading interp %删除线条

最终效果图如下:

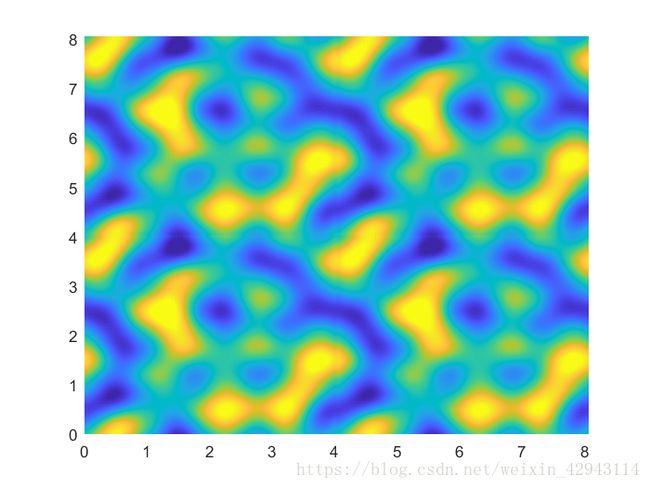
2.基于二维perlin噪声的分型噪声（Fractal noise）

其实分形噪声可以理解为将不同尺度的基本噪声叠加到一起。
这种噪声通常纹理更细腻，而且还有一定的自相似性，无论是细节还是大尺度方面都有很好的随机性。
下面是利用上述第1节中perlin噪声生成的不同尺度的噪声，更改了limx和limy的上限。

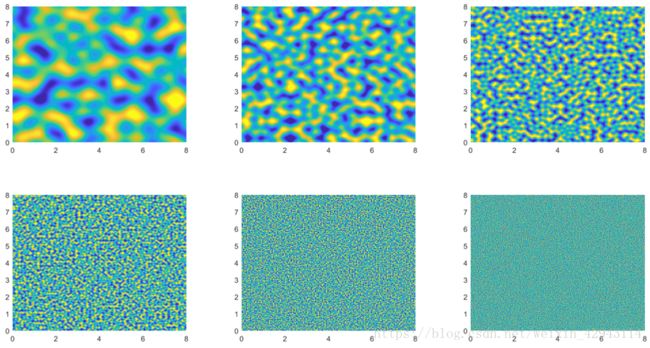
分型噪声的实现则是将上图中各个图像以一定权重比例加起来。由于为了保证不同尺度下zmat矩阵的可加性，最终计算点应该保持相同的数目，即limx和dx的变化要同倍数增长。以下是分型噪声的实现代码，用到了第一节中的simplexnoise2f.m函数。

maxx=4;maxy=4;%规定图像的范围上限
dx=1/64;dy=1/64;%规定图像的生成精度

%求出不同尺度下的zmat矩阵，注意要求不同zmat矩阵尺寸要相同
zmat1=simplexnoise2f([0 maxx],[0 maxy],dx,dy);
zmat2=simplexnoise2f([0 maxx*2],[0 maxy*2],dx*2,dy*2);
zmat3=simplexnoise2f([0 maxx*4],[0 maxy*4],dx*4,dy*4);
zmat4=simplexnoise2f([0 maxx*8],[0 maxy*8],dx*8,dy*8);
zmat5=simplexnoise2f([0 maxx*16],[0 maxy*16],dx*16,dy*16);
zmat6=simplexnoise2f([0 maxx*32],[0 maxy*32],dx*32,dy*32);

%绘制出当权重为0.5时的分型图像
figure(1)
q=0.5;
[xmat,ymat]=meshgrid(0:dx:maxx,0:dy:maxy);

subplot(2,3,1)
pcolor(xmat,ymat,zmat1)
shading interp
subplot(2,3,2)
pcolor(xmat,ymat,zmat1+zmat2*q)
shading interp
subplot(2,3,3)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2)
shading interp
subplot(2,3,4)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3)
shading interp
subplot(2,3,5)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3+zmat5*q^4)
shading interp
subplot(2,3,6)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3+zmat5*q^4+zmat6*q^5)
shading interp

%绘制出当权重为1时的分型图像
figure(2)
q=1;
[xmat,ymat]=meshgrid(0:dx:maxx,0:dy:maxy);
subplot(2,3,1)
pcolor(xmat,ymat,zmat1)
shading interp
subplot(2,3,2)
pcolor(xmat,ymat,zmat1+zmat2*q)
shading interp
subplot(2,3,3)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2)
shading interp
subplot(2,3,4)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3)
shading interp
subplot(2,3,5)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3+zmat5*q^4)
shading interp
subplot(2,3,6)
pcolor(xmat,ymat,zmat1+zmat2*q+zmat3*q^2+zmat4*q^3+zmat5*q^4+zmat6*q^5)
shading interp

最终结果图如下所示：
这是权重取0.5的时候，从初始图到最终分型细节图

这是权重取1的时候，从初始图到最终分型细节图

可以看到即使是只改变权重也可以让图形最终效果变得完全不一样。

3.可平铺的柏林噪声

对于柏林噪声图像的产生只与初始的随机梯度向量有关。所以如果初始梯度向量一致，则噪声也一致；如果随机梯度向量沿一个方向不断重复，则最终图像也会不断地重复。

所以本文可平铺柏林噪声的思路就是在边界上重复之前边界，即左边边界和右边边界梯度相同，上边边界和下边边界梯度相同。接下来是可平铺噪声的代码，除了uxmat,uymat的定义与之前有所改变，其余关键代码均相同。

%先定义变长大小，以及精度，以整数点为参考点
limx=[0 4];
limy=[0 4];
dx=1/16;
dy=1/16;
%定义网格，以及各随机向量矩阵
minx=limx(1);maxx=limx(2);
miny=limy(1);maxy=limy(2);
numx=maxx-minx+1;
numy=maxy-miny+1;
numx_z=(maxx-minx)/dx+1;
numy_z=(maxy-miny)/dy+1;

[uxmat,uymat]=randxymat(numx+1,numy+1);%生成随机向量阵，注意边缘所以多了一行一列
%这里是可平铺的关键，把边缘设置成相同
uxmat([end-1,end],:)=uxmat([1,2],:);uymat([end-1,end],:)=uymat([1,2],:);
uxmat(:,[end-1,end])=uxmat(:,[1,2]);uymat(:,[end-1,end])=uymat(:,[1,2]);
%这里是可平铺的关键，把边缘设置成相同

zmat=zeros(numy_z,numx_z);%预设随机云图
j=0;
for x=minx:dx:maxx
    j=j+1;
    k=0;
    for y=miny:dy:maxy
        k=k+1;
        %n00
        ddx=x-floor(x);
        ddy=y-floor(y);
        ux=uxmat(floor(y)-miny+1,floor(x)-minx+1);
        uy=uymat(floor(y)-miny+1,floor(x)-minx+1);
        n00=GridGradient(ux,uy,ddx,ddy);
        %n10
        ddx=x-floor(x)-1;
        ddy=y-floor(y);
        ux=uxmat(floor(y)-miny+1,floor(x)-minx+2);
        uy=uymat(floor(y)-miny+1,floor(x)-minx+2);
        n10=GridGradient(ux,uy,ddx,ddy);
        %n01
        ddx=x-floor(x);
        ddy=y-floor(y)-1;
        ux=uxmat(floor(y)-miny+2,floor(x)-minx+1);
        uy=uymat(floor(y)-miny+2,floor(x)-minx+1);
        n01=GridGradient(ux,uy,ddx,ddy);
        %u11
        ddx=x-floor(x)-1;
        ddy=y-floor(y)-1;
        ux=uxmat(floor(y)-miny+2,floor(x)-minx+2);
        uy=uymat(floor(y)-miny+2,floor(x)-minx+2);
        n11=GridGradient(ux,uy,ddx,ddy);
        %然后再加权
        n0=lerp(n00,n10,x-floor(x));
        n1=lerp(n01,n11,x-floor(x));
        zmat(k,j)=lerp(n0,n1,y-floor(y));
    end
end
zmat=zmat+0.5;
zmat(zmat>1)=1;zmat(zmat<0)=0;

%绘制两个周期的图像变化
[xmat,ymat]=meshgrid(minx:dx:2*maxx+dx,miny:dy:2*maxy+dy);
figure
pcolor(xmat,ymat,[zmat,zmat;zmat,zmat])
shading interp

function u=GridGradient(ux,uy,dx,dy)%数组相乘
    u=ux*dx+uy*dy;
end

function u=lerp(a,b,t)%权重相加
    tw=6*t.^5-15*t.^4+10*t.^3;%6*t.^5-15*t.^4+10*t.^3;%3*t.^2-2*t.^3;%
    u=(1-tw)*a + tw*b;
end

function [uxmat,uymat]=randxymat(numx,numy)%单位圆内随机向量
    num=numx*numy;
    uxmat=zeros(numy,numx);
    uymat=zeros(numy,numx);
    for j=1:num
        k=0;
        while k==0
            randxy=rand(1,2);
            if (randxy(1)-0.5)^2+(randxy(2)-0.5)^2<=0.25
                k=k+1;
                uxmat(j)=randxy(1);
                uymat(j)=randxy(2);
            end
        end
    end
    uxmat=(uxmat-0.5)*2;
    uymat=(uymat-0.5)*2;
end

下图就是可平铺图像的实现，x和y方向各平铺扩展1倍：

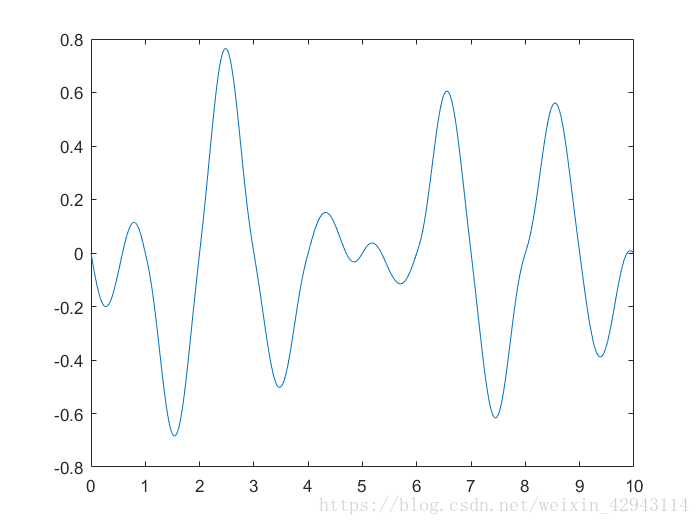
4.一维噪声的实现

4.1一维柏林噪声

同二维柏林噪声相比，一维噪声每个计算点对应随机梯度点（晶格点）数只有2个，而且随机梯度也是1维的。
和二维相比，依然是6个主要环节：
1。设定计算点网格
2。设定梯度点网格坐标以及相应随机梯度
3。设定空矩阵存放计算点
4。计算每个计算点的数值
5。求出方向向量与梯度向量的点积
6。加权算出最终计算点结果
代码如下

%1设定计算点网格
limx=[0 10];
dx=1/64;
x=limx(1):dx:limx(2);

%2求出梯度点的坐标以及梯度
numx=diff(limx)+1;
uxmat=rand(1,numx+1)*2-1;
%3设立空矩阵存放计算点
numx_z=diff(limx)/dx+1;
zmat=zeros(1,numx_z);

%4计算各个计算点的数值
for j=1:length(x)
    %5计算每个角点的点积
    %n0
    ddx=x(j)-floor(x(j));
    ux=uxmat(1,floor(x(j))-limx(1)+1);
    n0=(ux*ddx);
    %n1
    ddx=x(j)-floor(x(j))-1;
    ux=uxmat(1,floor(x(j))-limx(1)+2);
    n1=(ux*ddx);
    %6加权
    zmat(j)=lerp(n0,n1,x(j)-floor(x(j)));
    
end
zmat=zmat*2;
plot(x,zmat)

function u=lerp(a,b,t)%权重相加
    tw=6*t.^5-15*t.^4+10*t.^3;%6*t.^5-15*t.^4+10*t.^3;%3*t.^2-2*t.^3;%
    u=(1-tw)*a + tw*b;
end

图像如图所示

4.2动态一维柏林噪声

对于柏林噪声，所有动态n维噪声都可以用n+1维的柏林噪声来实现。具体实现方法就是就是把前n维当做图像，第n+1维当做时间轴进行变换。

在matlab里，如果已知一个二维柏林噪声矩阵zmat，可以依次画出矩阵每行的图像来进行一维噪声的实现。示意代码如下：

%实现动态1维函数的变化
% for j=1:numy_z
%     plot(minx:dx:maxx,zmat(j,:));
%     pause(0.2)%暂停功能，防止变化太快不显示
% end

这个道理也同样适用于动态2维噪声。

5.高维柏林噪声以及缺点

对于1维Perlin噪声，每个计算点只需要2个梯度点便可以计算；对于2维Perlin噪声，每个计算点需要包围这个点的矩形4角点来计算；对于3维，则需要8个立方体的角点梯度来计算；对于n维，则需要2^n个角点去计算每个点的数值，这大大增大了计算量。

因此Perlin本人于2002年又推出了一个新的梯度噪声计算方法，称为Simplex噪声。Simplex噪声就是解决Perlin噪声在高纬度下计算量指数型增大的这个问题而提出的，它的解决办法是化正方形网格为三角形网格。比如说，对于2维图形，Perlin噪声的正方形格点有4个，但是Simplex噪声的三角网格只有3个格点；对于3维图形，Perlin噪声的正方形格点有8个，但是Simplex噪声的三角网格只有4个格点（它的网格为正三棱锥）；对于n维图形，Perlin噪声的正方形格点有2^n个，但是Simplex噪声的三角网格只有n+1个格点。