【MATLAB模型】线性规划linprog 0-1规划intlinprog，非线性规划fmincon 罚函数法fminunc

 线性、非线性的区别： 

---

① linprog函数：

 求解线性规划问题，求目标函数的最小值，

[x,y]= linprog(c,A,b,Aeq,beq,lb,ub)

求最大值时，c加上负号：-c

② intlinprog函数：

求解混合整数线性规划问题，

[x,y]= intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)

与linprog相比，多了参数intcon,代表了整数决策变量所在的位置

---

1. matlab 线性规划：

（1）求最大值 ，加负号，因为默认是求最小值

%max 线性规划
clc;clear;

c=[2;3;-5];

a=[-2,5,-1;1,3,1]; 
b=[-10;12];
aeq=[1,1,1];
beq=7;

[x,y]=linprog(-c,a,b,aeq,beq,zeros(3,1))

 运行结果：

（2）求最小值

%min 线性规划
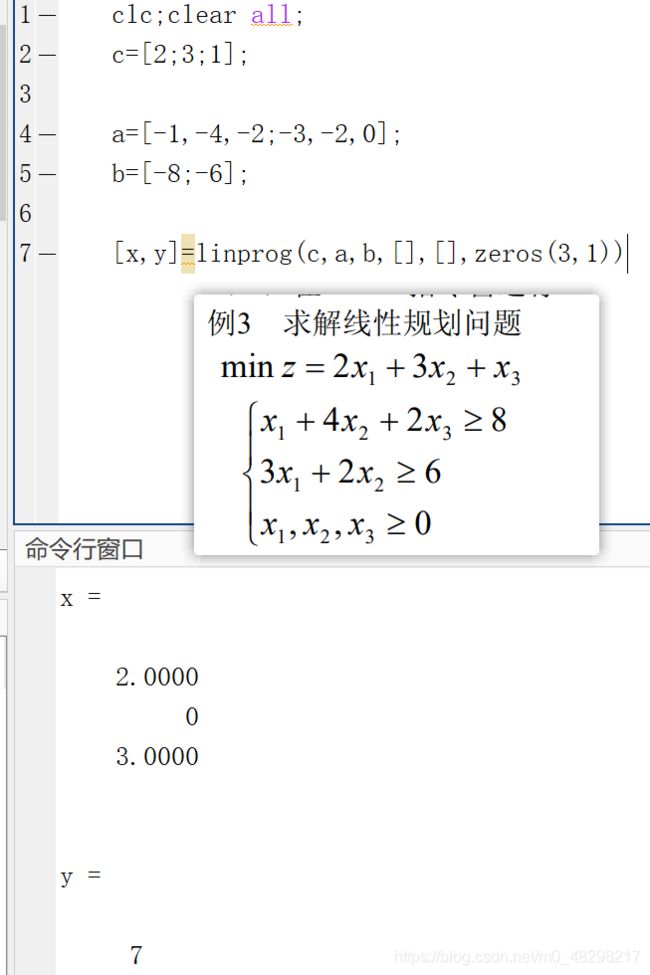
clc;clear all;
c=[2;3;1];

a=[-1,-4,-2;-3,-2,0];
b=[-8;-6];

[x,y]=linprog(c,a,b,[],[],zeros(3,1))

运行结果： 

 

（3）0-1规划 

clc;clear;
c=[6 2 3 5];
a=[-3 5 -1 -6;2 1 1 -1;1 2 4 5];
b=[-4;3;10];
intcon=[1 2 3 4];%与linprog相比，多了参数intcon,代表了整数决策变量所在的位置
lb=zeros(4,1);%0矩阵
ub=ones(4,1);%1矩阵
[x,fval]=intlinprog(-c,intcon,a,b,[],[],lb,ub)

运行结果：

x =

     1
     0
     1
     1


fval =

    14

---

 2. matlab 非线性规划：

 (1) fmincon函数求解非线性规划问题：

例子：

%fun1.m 定义目标函数 
function f=fun1(x);
f=sum(x.^2)+8;

%fun2.m定义非线性约束条件
function [g,h]=fun2(x); 
%g非线性不等式约束
g=[-x(1)^2+x(2)-x(3)^2 %化为小于等于号，所有项移项到左边
x(1)+x(2)^2+x(3)^3-20];
%h非线性等式约束
h=[-x(1)-x(2)^2+2 %所有项移项到左边
x(2)+2*x(3)^2-3];

主程序文件example2.m 如下：

 [x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')

运行结果：

x =

    0.5522
    1.2033
    0.9478


y =

   10.6511

(2) 罚函数法fminunc求解非线性规划问题

%fahanshu.m文件
function g=fahanshu(x);
%反函数法求解非线性规划问题
M=50000;
f=x(1)^2+x(2)^2+8;%对应约束条件的第1行
g=f-M*min(x(1),0)-M*min(x(2),0)...%对应约束条件的第四行
    -M*min(x(1)^2-x(2),0)+M*abs(-x(1)-x(2)^2+2);%对应约束条件的第2，3行

%修改罚函数的定义
%g=f-M*min(min(x),0)...%对应约束条件的第四行
    %-M*min(x(1)^2-x(2),0)+M*(-x(1)-x(2)^2+2)^2;%对应约束条件的第2，3行

主程序m文件： 

%% 在 Matlab 命令窗口输入
[x,y]=fminunc('fahanshu',rand(2,1))

运行结果： 

x =

    1.3040
    0.8342


y =

   10.3965