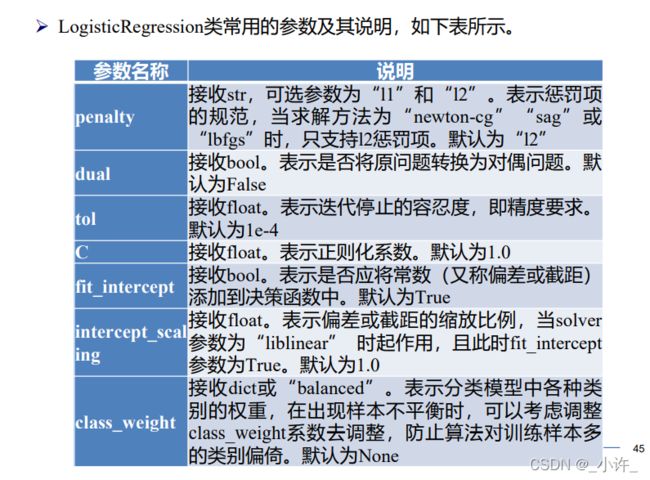
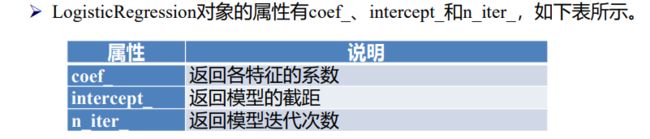
线性回归与逻辑回归算法
线性回归
线性回归原理
线性回归算法是一种预测连续变量模型的方法。他额基本思想是通过已知样本点的因变量和自变量的关系。设定一个数学模型,来拟合这些样本。也就是说线性回归通过样本寻找模型的过程。简单来说,假设现在有一些数据点,我们用一条直线对这些点进行拟合(该线称为最佳拟合直线),这个拟合过程就称作回归。
数学表示为:
自变量=x
因变量=y
线性回归模型:y=αx+β
构建回归模型是要用到的数学公式:
最小二乘法:(x0,y0是自变量,因变量的平均值)
b = y 0 − b ∗ x 0 b=y0-b*x0 b=y0−b∗x0
b = ∑ n = 1 N ( x i − x 0 ) ( y i − y 0 ) ∑ n = 1 N ( x i − x 0 ) 2 b=\frac{\sum_{n=1}^{N}{(xi-x0)(yi-y0)}}{\sum_{n=1}^{N}{(xi-x0)^2}} b=∑n=1N(xi−x0)2∑n=1N(xi−x0)(yi−y0)
案例:
import numpy as np
import matplotlib.pyplot as plt
import random
#随机库生成10个随机数
y=[]
for i in range(10):
a=random.random()*100
y.append(round(a,2))
print(y)
x=[]
for i in range(10):
a=random.random()*10
x.append(round(a,2))
print(x)
结果:
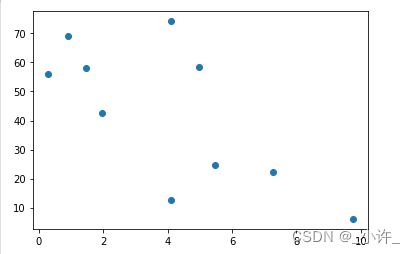
[24.53, 6.12, 22.25, 58.5, 56.14, 58.16, 74.19, 69.22, 42.43, 12.73]
[5.47, 9.74, 7.27, 4.96, 0.29, 1.45, 4.09, 0.91, 1.97, 4.1]
#散点图
plt.scatter(x,y)
plt.show()
# 构造回归模型
#求x0,y0
x0=round(np.mean(x),2)
y0=round(np.mean(y),2)
print(x0,y0)
#最小二乘法求b
#分子
def function1():
b=0
for x_,y_ in zip(x,y):
b0=((x_-x0)*(y_-y0))
b=b+b0
return b
print(function1())
#分母
def function2():
a=0
for x_ in x:
a0=(x_-x0)**2
a=a+a0
return a
print(function2())
#构建模型
b0=y0-(function1()/function2())*x0
def F(x):
return round((-x0*x+b0),2)
结果:
4.03 42.43
-459.16119999999995
80.67070000000001
#可视化模型
x_predict=[F(i) for i in x]
#print(x_predict)
plt.scatter(x,y)
plt.plot(x,x_predict)
plt.show()
机器学习的sklearn库实现:

在机器学习中常见的线性回归包括岭回归,套索回归和逻辑回归;岭回归最先用来处理特征数多余样本数的情况,能够减少不重要的参数,从而得到更好的估计;套索回归和岭回归相似,差别在于使用了不同的正则化项,最终都防止了过拟合的情况,套索回归可以将一些作用较小的特征训练为0,从而得到稀疏矩阵实现降维的目的。逻辑回归与线性回归的理论截然不同,其是解决分类问题的回归的到的模型是逻辑回归的分类器,模型的两侧代表不同的类别。
#糖尿病数据集实现线性回归模型
from sklearn.datasets import load_diabetes
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
diabetes=load_diabetes()
x_train,x_test,y_train,y_test=train_test_split(disabetes.data,disabetes.target,test_size=0.8)
line_model=LinearRegression().fit(x_train,y_train)
#输出系数和截距
a=line_model.coef_[0]
b=line_model.intercept_
print("回归方程:")
print("y=",a,"x","+",b)
#糖尿病共有10个特征每个特征精心线性回归
print(line_model.coef_)
结果:
回归方程:
y= 41.99458340278894 x + 154.450704544504
[ 41.9945834 -77.86156968 592.1697319 371.42603326
1777.13864509 -1629.15453734 -981.68978861 -231.06530675
76.85762741 -141.81995976]
可以看出该数据集有10个特征,coef_表示斜率参数有10个是10个特征的斜率列表。intercept_是截距。
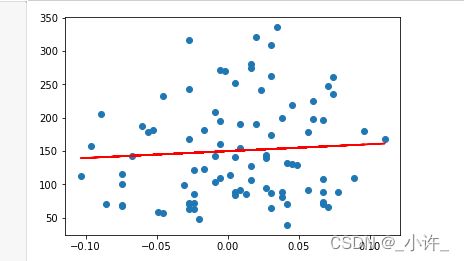
观察数据集,需要对每个特征都进行线性回归(x轴是特征,y轴是类别。所有特征决定一个类别,所以单个特征对应唯一类别):
#对每个类别回归可视化
#第一个特征回归
plt.scatter(x_train[:,0:1],y_train) # x_train[:,0:1]表示取出第一个特征的所有值
plt.plot(x_train[:,0:1],(line_model.coef_[0]*x_train[:,0:1]+b),color='red')
plt.show()
#第二个特征回归
plt.scatter(x_train[:,1],y_train) # x_train[:,1]表示取出第二个特征的所有值
plt.plot(x_train[:,1],(line_model.coef_[1]*x_train[:,1]+b),color='red')
plt.show()
x_train[:,1]表示取出训练集中某列的所有值,即某个特征line_model.coef_[1]*x_train[:,1]+b是回归方程。其他特征不在赘述。更改相关参数即可。
回归模型的相关参数:

套索回归(Lasso)和岭回归(Ridge):
#同数据集实现套索和岭回归
from sklearn.linear_model import Lasso,Ridge
lasso_model=Lasso().fit(x_train,y_train)
ridge_model=Ridge().fit(x_train,y_train)
#糖尿病共有10个特征每个特征回归参数
lasso_b=lasso_model.intercept_
ridge_b=ridge_model.intercept_
print(lasso_model.coef_)
print(ridge_model.coef_)
结果:
[ 0. 0. 374.14730981 136.60701446 0.
0. -156.27971376 17.6345838 202.6373388 0. ]
[ 31.56918273 27.69183081 133.19344079 106.56506708 11.89302661
22.42204053 -108.11257191 100.44909711 105.62935807 90.38474187]
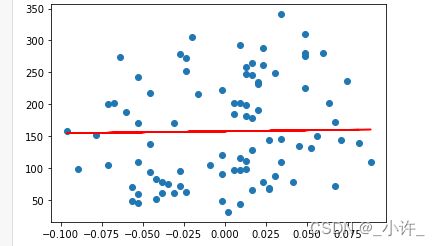
#第Lasso特征回归
plt.scatter(x_train[:,0:1],y_train) # x_train[:,0:1]表示取出第一个特征的所有值
plt.plot(x_train[:,0:1],(lasso_model.coef_[0]*x_train[:,0:1]+lasso_b),color='red')
plt.show()
#第Ridge特征回归
plt.scatter(x_train[:,0:1],y_train) # x_train[:,0:1]表示取出第一个特征的所有值
plt.plot(x_train[:,0:1],(ridge_model.coef_[0]*x_train[:,0:1]+ridge_b),color='red')
plt.show()
其他特征不再赘述。
逻辑回归
逻辑回归原理:
逻辑回归(Logistic Regression)是分类问题,利用Logistic回归进行分类的主要思想是:根据现有数据对分类边界线建立回归公式,以此进行分类。是一种用于解决二分类(0 or 1)问题的机器学习方法。虽然有回归但却是分类算法。

用上面的案例数据实现逻辑回归:
案例中的回归模型:
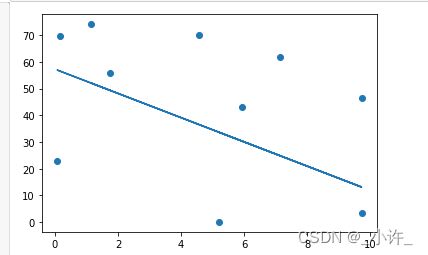
构建逻辑回归模型:
下图是案例的回归模型图,对该案例进行逻辑回归即二分类,在直线上方为1类别,下方为2类别。

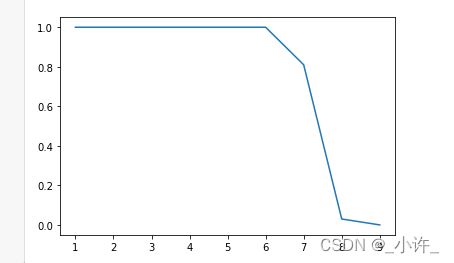
#构造sigmoid函数,由图可以看出范围始终在[0,1]
#得到了回归方程F(x),有sigmoid函数转化为逻辑回归
#sigmoid函数:y=1/e^(-F(x)) e是自然对数的底数
import math
def G(x):
return round(1/(1+(math.e)**(-F(x))),2)
x00=range(1,10)
y00=[G(i) for i in x00]
plt.plot(x00,y00)
plt.show()
sigmoid函数实际上就是将不同点到直线的距离转化为概率。
#用距离分类
chazhi=[]
for i,j in zip(x,y):
a=j-F(i)
chazhi.append(round(a,2))
print(chazhi)
gailv=[]
for i in chazhi:
if i>0:
gailv.append(1)
else:
gailv.append(0)
print(gailv)
#用sigmoid函数分类
sigmoid=[]
for i in x:
if 0<(G(i))<=1:
sigmoid.append(1)
else:
sigmoid.append(0)
print(sigmoid)
结果:
[41.56, 45.52, 56.17, 0.73, 55.79, 30.4, -4.74, 55.69, -24.95, 87.65]
[1, 1, 1, 1, 1, 1, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 0, 1, 1, 1, 0]
机器学习实现逻辑分类:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
diabetes=load_diabetes()
x_train,x_test,y_train,y_test=train_test_split(diabetes.data,diabetes.target,test_size=0.2) #只用前两个属性
line_model=LogisticRegression().fit(x_train,y_train)
score=line_model.score(x_test,y_test)
print(score)
结果:
0.9