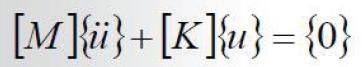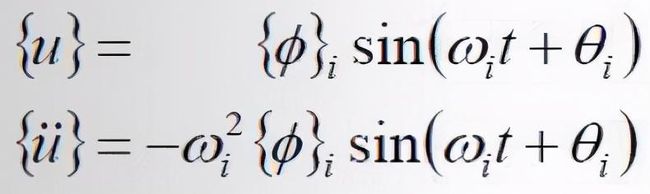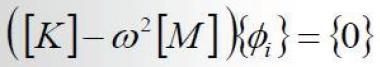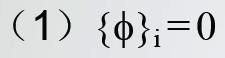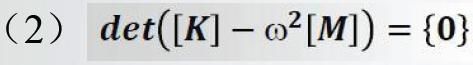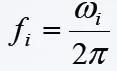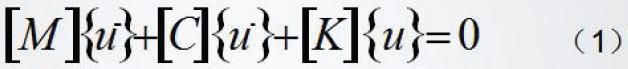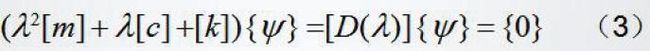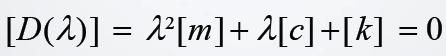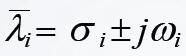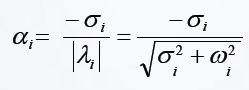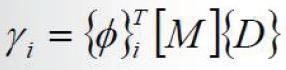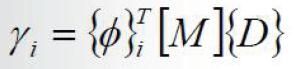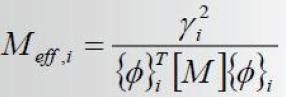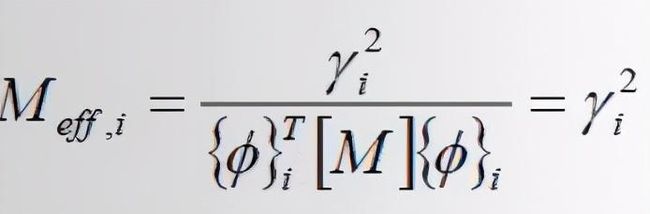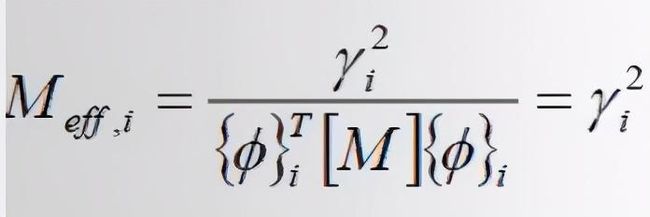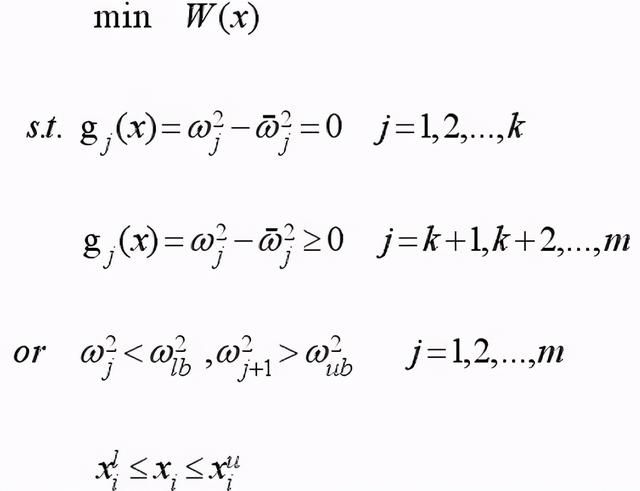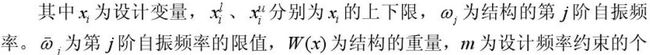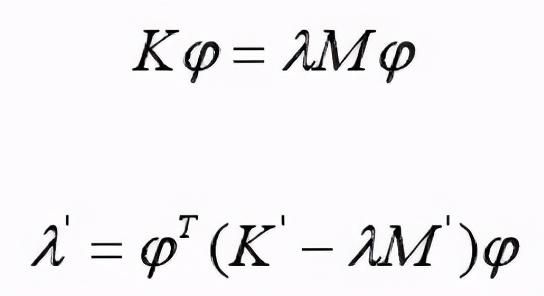设计一个名为complex的类来表示复数_CAE必修课:结构动力优化设计
01
结构动力优化设计简介
工程结构在其工作期间将经常性地受到风浪、地震、振动设备等各种外界激励的影响,本质上讲,工程结构所受到的环境载荷都是动载荷,其正常服役性能会受到动力破坏或损伤的影响。船舶在正常服役中会受到主机、螺旋桨的振动和波浪的冲击等外界载荷的作用,海洋平台在其使用期间也要受到复杂的环境荷载和各种振动设备的影响,船舶、海洋平台结构在这些外界载荷的作用下,将会发生不同程度的振动。如若振动过大,则可导致结构产生疲劳破坏,相关人员的工作效率也会受到影响,甚至还会损害到人员的身体健康,仪器和设备的正常使用也很难以得到保证。欲使结构和设备在动力载荷作用下的相应力学特性得到改善,使其振动得到有效控制和在正常工作时能一直保持较好的性能,对其进行结构动力优化设计是非常有效的方法。
结构的动力优化设计相对于结构的动力分析来说,是其反问题或逆问题,相比正问题而言,其理论求解要复杂和困难得多。在结构动力优化设计中,同时涉及到结构动力学基本理论、灵敏度分析、结构有限元建模、结构重分析、数学优化算法、软件编程和实际工程应用等诸多方面,是诸多学科相互交叉、有机结合的产物。它包括近代的结构动力学、数学优化方法、数值计算方法、结构有限元法以及程序设计等,是现代工程结构设计领域中的一个新兴的分支。结构动力优化设计的主要任务是:根据在实际中对结构要求的不同,构建相应的结构动力分析与优化设计理论模型,把相关算法语言、各种优化数学算法与结构在动载荷作用下的分析计算方法相融合,对结构的布局参数、尺寸参数、材料参数等进行优化配置,达到改善结构动力特性、降低结构振动的目的。
根据优化目标的不同,结构动力优化可以分成两个部分:
即针对结构动力特性的优化设计和针对结构动力响应的优化设计。其中,针对结构动力特性的优化设计研究主要是以结构的固有频率、振型、阻尼和刚度与质量分布等方面为目标的优化设计研究。其中最早涉及到的课题是以结构固有频率为目标或约束的优化设计。设计阶段若通过合理配置结构的相应参数,使结构的固有频率远离激励频率,能够提高结构在正常工作时的安全性能。另外,针对结构动力响应的优化设计也是结构优化设计的重要组成部分,它主要是以结构在动载荷作用下振动响应的物理量,如:速度、加速度、振动功率流、声辐射能量等为目标或约束的结构优化设计。结构动力响应优化设计因为同时涉及到结构动力特性和动力响应分析计算以及相应数学优化算法,与结构动力特性优化设计相比较,其求解难度要更高,计算量更大。现阶段,结构的动力优化主要是指结构动力特性的优化设计。
02
结构动力优化设计的基本原理
2.1 结构模态分析方法
模态计算是用来计算线性结构的动力学特性:
-结构的固有频率;
-结构的模态振型;
-振型参与系数
-有效质量
模态分析所有动力学计算的最基础和最重要的分析;通过模态分析可以使结构避免共振或让结构在指定的频率下振动。
模态计算的假设和限制条件:
-结构是线性的,即具有恒定的总体质量矩阵和总体刚度矩阵
-结构没有外载荷(力,温度,压力等),即结构是自由振动。
2.1.1 无阻尼模态分析理论:
无阻尼线性结构自由振动的控制方程:
假设结构的运动简谐运动:
将结构运动的位移和速度,代入到控制方程中,可得
以下两种情况可以满足上述方程
-表明结构没有振动,这个情况不考虑舍去
这个是一个特征值问题,可以求解出n个方程的根
这些根是这个方程的特征值;
对于每一根(特征值),都对应着一个特征向量
ANSYS采用下式输出计算的固有频率:
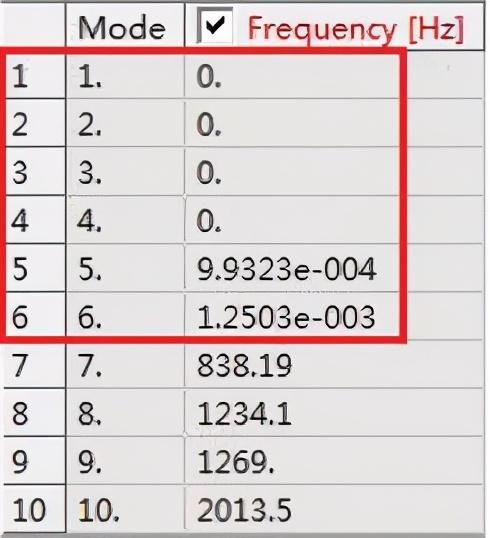
其中:fi的单位为Hz,即转/秒。如果模型的约束不足导致产生刚体运动,则总体刚度矩阵[K]为半正定型,则会出现固有频率为0的情况。
2.1.2 有阻尼模态分析理论:
有阻尼模态分析中假设结构没有外力作用,则控制方程变为
设解为
代入方程(1)得
矩阵
称为系统的特征矩阵。方程(3)是一个“二次特征值”问
题,要(3)式有非零解的充要条件为
对于包含陀螺效应的旋转软化结构或需考虑阻尼的结构,则使用QR的表达式:Damped法求解模态振型和复特征值。特征值
的表达式
复数特征值的实部;
复数特征值的虚部
特征值的虚部
代表系统的稳态角频率。特征值的实部
代表系统的稳定性 。
模态阻尼比由下式给出:
它的物理意义是实际阻尼与临界阻尼之比对数衰减率表示任意连续位移峰值的比值。它的表达式如下:
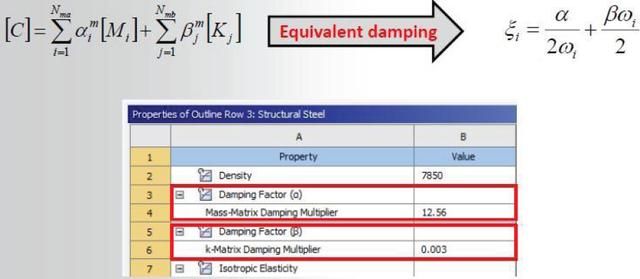
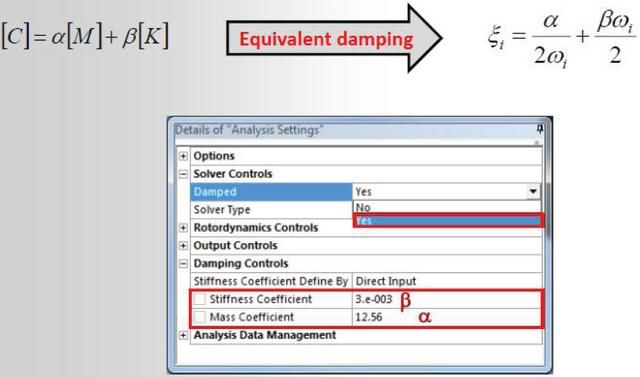
考虑阻尼的模态计算中的完整阻尼矩阵:
对于阻尼矩阵,程序支持材料阻尼和总体阻尼控制,当需要考虑模型中不同的材料阻尼时,用户可以在工程数据模块为不同的材料定义刚度阻尼系数和质量阻尼系数
2.模态分析理论和术语
2.2 有阻尼模态分析理论:
用户可以在进入Model中定义结构的总体阻尼特性:
2.1.2 有阻尼模态分析理论:
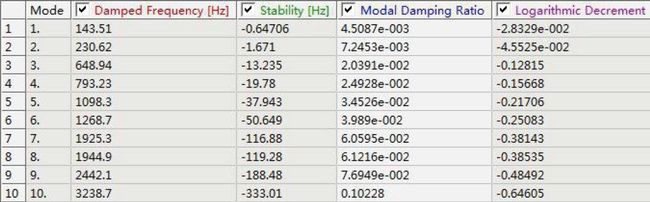
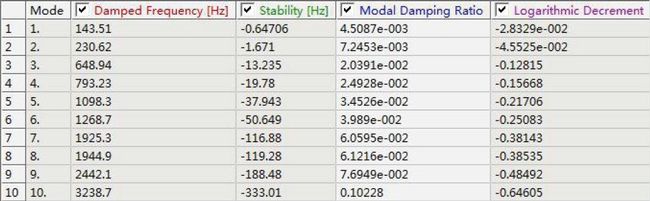
考虑阻尼的模态计算输出的特征值是复数:
模态计算的方程数=无约束的节点*节点的自由度,即能够提取的最大模态阶数。
2.1.3固有频率和模态振型
在模态计算中:
1.特征值等于结构自然频率(固有频率)值的平方;
2.特征向量,对应于结构的振型,即结构的每个固有频率都关联一个模态形状向量
3.模态振型可以关于质量矩阵进行归一化:
模态振型也可以关于单位矩阵进行归一化,基于该归一化方法可以比较各个节点发生共振时的相对位移量,在关于单位矩阵进行归一化时,将模态的最大特征向量设置为1:
Workbench后处理显示的关于质量矩阵归一化的结果;
由于模态计算结果是一个归一化的相对值,因此只有每个节点自由度的振动形状具有真实意义。
特征值的平凡根等于结构的固有频率(rad/s)
ANSYS Workbench输入和输出的固有频率的单位为Hz,因为输入和输出时候已经除以了2π。
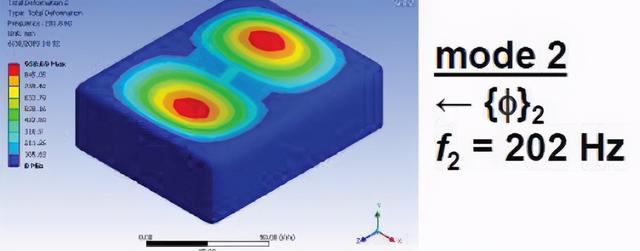
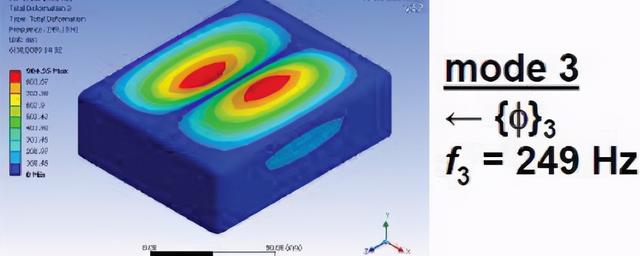
模态计算中的特征向量表征了结构的模态振型,如图所示该形状即为假设结构按照频率249Hz振动时的形状。
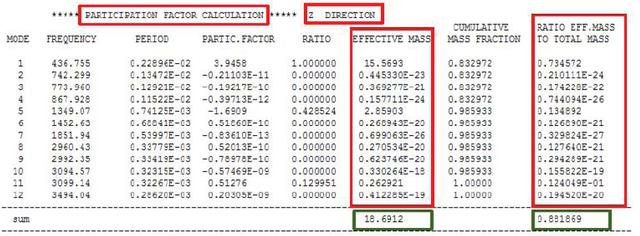
2.1.4.参与系数,有效质量
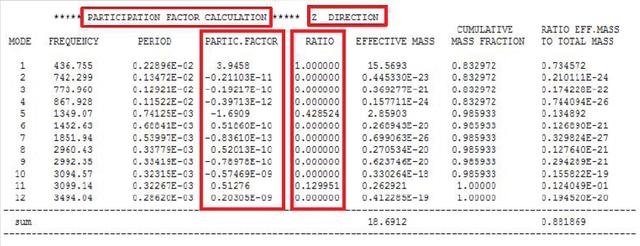
模态计算后除了能够获取结构的固有频率和振型外,还有参与系数与有效质量,其中参与系数的计算公式:
其中,{D}为总体笛卡尔坐标系中三个平动和三个转动的单位位移谱。
(1)参与系数是表征每阶模态每个方向质量运动的总和,即在特定方向上某个振型在多大程度上参与了振动)
(2)某一个方向的参与系数值越大,则表明如果在这个方向受到动载荷的作用下,则结构的振动响应越大。
(3)比值(Ratio),就是某个方向所有模态阶数的参与系数关于最大的参与系数进行归一化的比值。
参与系数的计算公式:
模态计算中的有效质量计算公式:
由于程序模态计算时,各个振型关于质量矩阵进行归一化,即
则,有效质量可简化为
-理想情况下,在每个方向的所有有效质量之和等于结构的总质量,但是这个取决于模态计算提出的模态阶数;
-有效质量与结构总质量的比值对于确定提取的模态数量是否足够,非常有帮助。
模态计算中的有效质量计算公式:
2.1.5 模态的提取方法
在大多数情况下,建议用户选用 Program Controlled选项,程序会自 动优化进行选择算法。
(1)Direct-Block Lanczos
-能够处理对称矩阵;
-是一种功能强大的方法,当提取中型到大型模型(50000 ~ 100000 个自由度)的大量振型时(40+),这种方法很有效;
-经常应用在具有实体单元或壳单元的模型中;
-可以很好地处理刚体振型;
-需要较高的内存。
(2)Iterative-PCG Lanczos
-能够处理对称矩阵,但是不用于求解屈曲模态;
-适合求解中等到大规模的模态计算问题,提取的模态阶数高于100阶;
-适合于网格划分形状较好的三维实体单元;
(3)Unsymmetric
-能够处理非对称矩阵;
-模态计算中使用完整的刚度和质量矩阵;
-适合求解K和M为非对称矩阵的问题,如流-固耦合的振动,声学振动;
-计算以复数表示的特征值和特征向量:
--实数部分就是自然频率;
--虚数部分表示稳定性,负值表示稳定,正值表示不确定。
(4)Supernode
-能够处理对称矩阵,但是不用于求解屈曲模态;
-适合求解大规模的模态计算问题,提取的模态阶数高于100000阶;
-主要应用于二维平面,壳体/梁结构(提取模态阶数高于100)和三维实体
结构(提取模态阶数高于250);
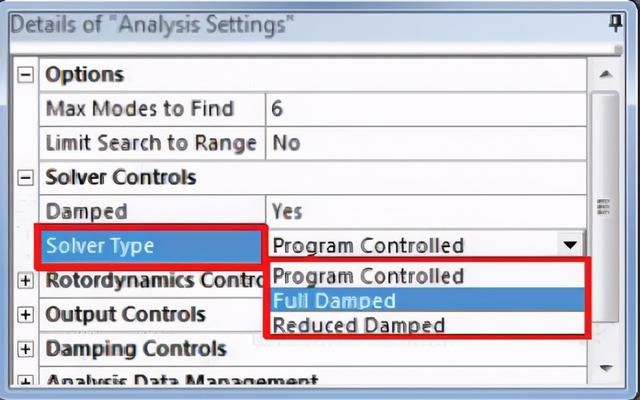
如果结构中存在阻尼,则将阻尼选项 设置为yes,然后选择
相应的方法进 行求解。
(5)Full Damped
(6) Reduced Damped
QR阻尼法能够很好地求解大阻尼系统模态解,阻尼可以是任意阻尼类型,即 无论是比例阻尼或非比例阻尼。由于该方法的计算精度取决于提取的模态数目,所以建议提取足够多的基频模态,特别是阻尼较大的系统更应当如此,这样才能保证得到好的计算结果。该方法不建议用于提取临界阻尼或过阻尼 系统的模态。该方法输出实部和虚部特征值(频率),但仅仅输出实特征向量(模态振型)。
2.2 结构动力优化模型
以结构重量为目标函数,以某阶频率或频率禁区
为约束,要求重量最小。
数。其中设计变量的选择根据各种优化问题的具体情况,如杆件的截面面积、板的厚度设计变量梁的截面惯性矩等等,如果考虑形状的优化,节点坐标也可以作为在动力问题中,非结构质量的位置和大小也可以作为设计变量加以考虑。实际工程优化问题还应同时考虑应力、位移等其他的约束条件。
2.3 频率优化中的灵敏度分析
灵敏度分析是一种度量。它是一种评价因设计变量或参数的改变而引起结构响应特性变化率的方法。结构系统灵敏度的研究是一个很特别的领域,它是当前计算力学和结构工程领域的主要研究方向之一。灵敏度分析是结构优化设计方法的基础。在对离散化的结构模型进行优化时,除非应用少数几种比较初等的方法,否则,不论是用准则设计法还是数学规划法,在修改结构的尺寸使之向更优方向变化时,都必须作灵敏度分析。在结构动力优化设计中,寻求有效的结构自振频率及振型关于设计变量灵敏度的方法十分重要。关于频率优化中特征值和特征向量的灵敏度的求解,特征根问题可以描述如下:
关于频率优化中特征值和特征向量的灵敏度的求解,特征根问题可以描述如下:
其中,K为结构的刚度矩阵,M为结构的质量矩阵,
为特征根,
为特征向量,K’、M’分别为刚度矩阵和质量矩阵关于设计变量的导数。
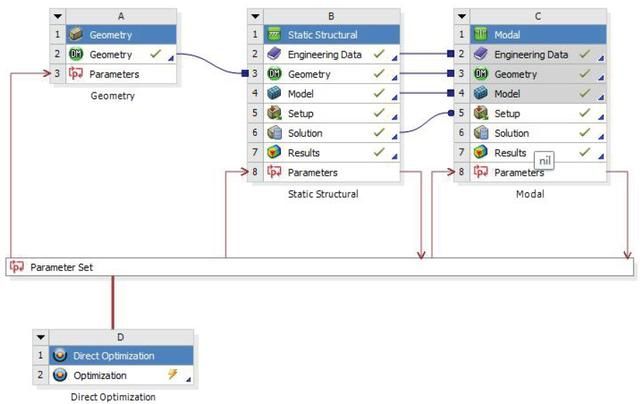
03
结构动力优化设计的ANSYS实现