逆天了!用Numpy开发深度学习框架,透视神经网络训练过程
哈喽,大家好。
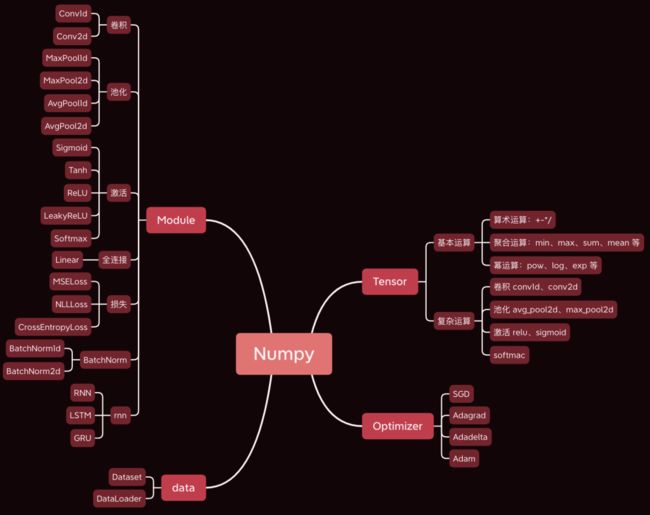
今天给大家分享一个非常牛逼的开源项目,用Numpy开发了一个深度学习框架,语法与 Pytorch 基本一致。
今天以一个简单的卷积神经网络为例,分析神经网络训练过程中,涉及的前向传播、反向传播、参数优化等核心步骤的源码。
使用的数据集和代码已经打包好,文末有获取方式。
1. 准备工作
先准备好数据和代码。
1.1 搭建网络
首先,下载框架源码,地址:https://github.com/duma-repo/PyDyNet
git clone https://github.com/duma-repo/PyDyNet.git
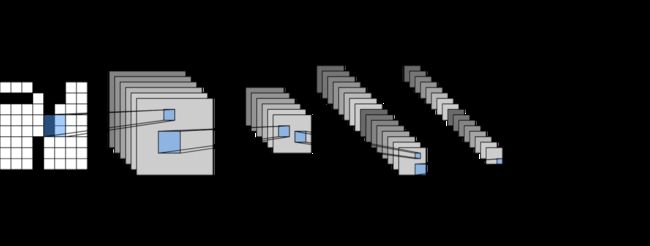
搭建LeNet卷积神经网络,训练三分类模型。
在PyDyNet目录直接创建代码文件即可。
from pydynet import nn
class LeNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avg_pool = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
self.sigmoid = nn.Sigmoid()
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 3)
def forward(self, x):
x = self.conv1(x)
x = self.sigmoid(x)
x = self.avg_pool(x)
x = self.conv2(x)
x = self.sigmoid(x)
x = self.avg_pool(x)
x = x.reshape(x.shape[0], -1)
x = self.fc1(x)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)
return x
可以看到,网络的定义与Pytorch语法完全一样。
我提供的源代码里,提供了 summary 函数可以打印网络结构。
1.2 准备数据
训练数据使用Fanshion-MNIST数据集,它包含10个类别的图片,每个类别 6k 张。
为了加快训练,我只抽取了前3个类别,共1.8w张训练图片,做一个三分类模型。
1.3 模型训练
import pydynet
from pydynet import nn
from pydynet import optim
lr, num_epochs = 0.9, 10
optimizer = optim.SGD(net.parameters(),
lr=lr)
loss = nn.CrossEntropyLoss()
for epoch in range(num_epochs):
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with pydynet.no_grad():
metric.add(l.numpy() * X.shape[0],
accuracy(y_hat, y),
X.shape[0])
训练代码也跟Pytorch一样。
下面重点要做的就是深入模型训练的源码,来学习模型训练的原理。
2. train、no_grad和eval
模型开始训练前,会调用net.train。
def train(self, mode: bool = True):
set_grad_enabled(mode)
self.set_module_state(mode)
可以看到,它会将grad(梯度)设置成True,之后创建的Tensor是可以带梯度的。Tensor带上梯度后,便会将其放入计算图中,等待求导计算梯度。
而下面的with no_grad(): 代码
class no_grad:
def __enter__(self) -> None:
self.prev = is_grad_enable()
set_grad_enabled(False)
会将grad(梯度)设置成False,这样之后创建的Tensor不会放到计算图中,自然也不需要计算梯度,可以加快推理。
我们经常在Pytorch中看到net.eval()的用法,我们也顺便看一下它的源码。
def eval(self):
return self.train(False)
可以看到,它直接调用train(False)来关闭梯度,效果与no_grad()类似。
所以,一般在训练前调用train打开梯度。训练后,调用eval关闭梯度,方便快速推理。
2. 前向传播
前向传播除了计算类别概率外,最最重要的一件事是按照前传顺序,将网络中的 tensor 组织成计算图,目的是为了反向传播时计算每个tensor的梯度。
tensor在神经网络中,不止用来存储数据,还用计算梯度、存储梯度。
以第一层卷积操作为例,来查看如何生成计算图。
def conv2d(x: tensor.Tensor,
kernel: tensor.Tensor,
padding: int = 0,
stride: int = 1):
'''二维卷积函数
'''
N, _, _, _ = x.shape
out_channels, _, kernel_size, _ = kernel.shape
pad_x = __pad2d(x, padding)
col = __im2col2d(pad_x, kernel_size, stride)
out_h, out_w = col.shape[-2:]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
col_filter = kernel.reshape(out_channels, -1).T
out = col @ col_filter
return out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
x是输入的图片,不需要记录梯度。kernel是卷积核的权重,需要计算梯度。
所以,pad_x = __pad2d(x, padding) 生成的新的tensor也是不带梯度的,因此也不需要加入计算图中。
而kernel.reshape(out_channels, -1)产生的tensor则是需要计算梯度,也需要加入计算图中。
下面看看加入的过程:
def reshape(self, *new_shape):
return reshape(self, new_shape)
class reshape(UnaryOperator):
'''
张量形状变换算子,在Tensor中进行重载
Parameters
----------
new_shape : tuple
变换后的形状,用法同NumPy
'''
def __init__(self, x: Tensor, new_shape: tuple) -> None:
self.new_shape = new_shape
super().__init__(x)
def forward(self, x: Tensor) -> np.ndarray:
return x.data.reshape(self.new_shape)
def grad_fn(self, x: Tensor, grad: np.ndarray) -> np.ndarray:
return grad.reshape(x.shape)
reshape函数会返回一个reshape类对象,reshape类继承了UnaryOperator类,并在__init__函数中,调用了父类初始化函数。
class UnaryOperator(Tensor):
def __init__(self, x: Tensor) -> None:
if not isinstance(x, Tensor):
x = Tensor(x)
self.device = x.device
super().__init__(
data=self.forward(x),
device=x.device,
# 这里 requires_grad 为 True
requires_grad=is_grad_enable() and x.requires_grad,
)
UnaryOperator类继承了Tensor类,所以reshape对象也是一个tensor。
在UnaryOperator的__init__函数中,调用Tensor的初始化函数,并且传入的requires_grad参数是True,代表需要计算梯度。
requires_grad的计算代码为is_grad_enable() and x.requires_grad,is_grad_enable()已经被train设置为True,而x是卷积核,它的requires_grad也是True。
class Tensor:
def __init__(
self,
data: Any,
dtype=None,
device: Union[Device, int, str, None] = None,
requires_grad: bool = False,
) -> None:
if self.requires_grad:
# 不需要求梯度的节点不出现在动态计算图中
Graph.add_node(self)
最终在Tensor类的初始化方法中,调用Graph.add_node(self)将当前tensor加入到计算图中。
同理,下面使用requires_grad=True的tensor常见出来的新tensor都会放到计算图中。
经过一次卷积操作,计算图中会增加 6 个节点。
3. 反向传播
一次前向传播完成后,从计算图中最后一个节点开始,从后往前进行反向传播。
l = loss(y_hat, y)
l.backward()
经过前向网络一层层传播,最终传到了损失张量l。
以l为起点,从前向后传播,就可计算计算图中每个节点的梯度。
backward的核心代码如下:
def backward(self, retain_graph: bool = False):
for node in Graph.node_list[y_id::-1]:
grad = node.grad
for last in [l for l in node.last if l.requires_grad]:
add_grad = node.grad_fn(last, grad)
last.grad += add_grad
Graph.node_list[y_id::-1]将计算图倒序排。
node是前向传播时放入计算图中的每个tensor。
node.last 是生成当前tensor的直接父节点。
调用node.grad_fn计算梯度,并反向传给它的父节点。
grad_fn其实就是Tensor的求导公式,如:
class pow(BinaryOperator):
'''
幂运算算子,在Tensor类中进行重载
See also
--------
add : 加法算子
'''
def grad_fn(self, node: Tensor, grad: np.ndarray) -> np.ndarray:
if node is self.last[0]:
return (self.data * self.last[1].data / node.data) * grad
return后的代码其实就是幂函数求导公式。
假设y=x^2,x的导数为2x。
4. 更新参数
反向传播计算梯度后,便可以调用优化器,更新模型参数。
l.backward()
optimizer.step()
本次训练我们用梯度下降SGD算法优化参数,更新过程如下:
def step(self):
for i in range(len(self.params)):
grad = self.params[i].grad + self.weight_decay * self.params[i].data
self.v[i] *= self.momentum
self.v[i] += self.lr * grad
self.params[i].data -= self.v[i]
if self.nesterov:
self.params[i].data -= self.lr * grad
self.params是整个网络的权重,初始化SGD时传进去的。
step函数最核心的两行代码,self.v[i] += self.lr * grad 和 self.params[i].data -= self.v[i],用当前参数 - 学习速率 * 梯度更新当前参数。
这是机器学习的基础内容了,我们应该很熟悉了。
一次模型训练的完整过程大致就串完了,大家可以设置打印语句,或者通过DEBUG的方式跟踪每一行代码的执行过程,这样可以更了解模型的训练过程。