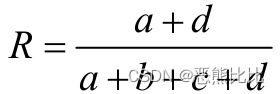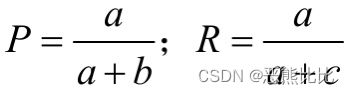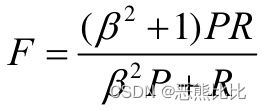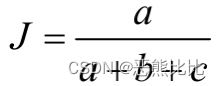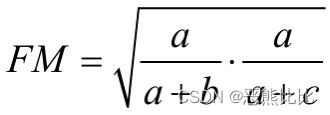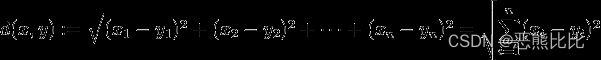K-means聚类算法原理及实现

1.聚类分析

1.1概念

聚类分析，也称为分割分析或分类分析，可将样本数据分成一个个组（即簇）。同一簇中的对象是相似的，不同簇中的对象则明显不同。

Statistics and Machine Learning Toolbox™ 提供了几种聚类方法和相似性度量（也称为距离度量）来创建簇。此外，簇计算可以按照不同的计算标准确定数据的最佳簇数。

1.2 K 均值和层次聚类

K 均值聚类是一种分区方法，它将数据中的观测值视为具有位置和相互间距离的对象。它将对象划分为 K 个互斥簇，使每个簇中的对象尽可能彼此靠近，并尽可能远离其他簇中的对象。每个簇的特性由其质心或中心点决定。当然，聚类中使用的距离通常不代表空间距离。

层次聚类是通过创建聚类树，同时在多个距离尺度内调查数据分组的一种方法。与 K-均值法不同，树并不是一组簇的简单组合，而是一个多级层次结构，较低级别的簇在相邻的更高级别合并成新的簇。使用这种方法，可以选择最适合您的应用场景的聚类尺度或级别。

Fisher 鸢尾花数据的聚类分析：
https://ww2.mathworks.cn/help/stats/cluster-analysis-example.html

2. 聚类分析的度量

度量指标对聚类结果进行评判；

• 外部指标：以事先指定的聚类模型为参考；
• 内部指标：参与聚类的样本；

2.1 外部指标

对含有n个样本的数据集S，其中两个样本点x1,x2，假定通过聚类给出的簇划分结果为C，外部参考模型给出的结果为P;对于x1,x2存在四种关系：

• SS:x1、x2在C和P中属于相同的簇；
• SD:在C中相同，P中不同；
• DS:C中不同，P中相同；
• DD:x1、x2在C和P中属于不同的簇；

a,b,c,d分别表示上述关系对应的关系数目，x1和x2存在且唯一存在上四种关系之一；

a+b+c+d = n(n-1)/2；

外部度量指标：

1. Rand统计量

2. F值（F-measure）
   
   //P表示准确率；
   //R表示召回率
   

3. Jaccard 系数
   

4. FM指数
   

• 以上四个度量结果越大，表明聚类结果和参考模型的划分结果越吻合；

2.2 内部度量

2.2.1 样本点和聚类中心的距离度量

1. 欧氏距离
   

计算欧氏空间两个点之间的距离

3. 曼哈顿距离
   

也称城市街区距离度量，相当于沿着两个街道行驶的距离（实际行驶距离）

4. 切比雪夫距离

向量空间距离的度量，相当于象棋盘移动格子之间的距离

5. 可明夫斯基距离

欧氏和曼哈顿的推广

聚类性能度量

1. 紧密性

指每个样本到聚类中心的平均距离

2. 分隔度

是个簇的簇心之间的平均距离。分割度值越大说明簇间间隔越远，分类效果越好，即簇间相似度越低。

3. 戴维森保丁指数

衡量任意两个簇的簇内距离之后与簇间距离之比。该指标越小表示簇内距离越小，簇内相似度越高，簇间距离越大，簇间相似度低。

4. 邓恩指数

任意两个簇的样本点的最短距离与任意簇中样本点的最大距离之商。该值越大，聚类效果越好。

5. 轮廓系数

对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1]，同类别样本距离越相近不同类别样本距离越远，分数越高。

3.K-means概念

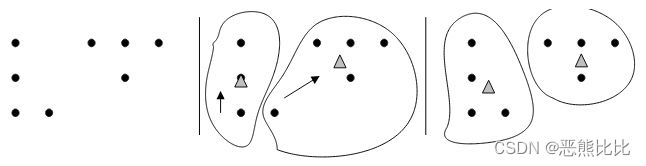
k-means算法 ：又名k均值算法，是基于划分的聚类，K-means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。

算法思想：先从样本集中随机选取 k个样本作为簇中心，并计算所有样本与这 k个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。

• 四个要点：
     （1）簇个数 k 的选择
     （2）各个样本点到“簇中心”的距离
     （3）根据新划分的簇，更新“簇中心”
     （4）重复上述2、3过程，直至"簇中心"没有移动
   
  优点：
  计算速度快、易于理解；

4.K-means算法步骤

• K值的选择： 选取K个簇类的质心（通常为随机）；
• 距离度量： 计算剩余样本到各质心的距离（一般为欧氏距离），归类到相互距离最小的质心所在的簇；
• 新质心计算： 剩余点归类完毕后计算新质心，然后再重新计算各样本到质心的距离；
• 停止条件： 迭代计算完毕所有的样本点的距离，当样本的距离划分情况基本不变时，说明已经到最优解，返回结果；

5.K-means案例1(python代码)

参考链接： https://blog.csdn.net/qq_43741312/article/details/97128745

代码：

import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


# 计算欧拉距离
def calcDis(dataSet, centroids, k):
    clalist = []
    for data in dataSet:
        diff = np.tile(data, (k,
                              1)) - centroids  # 相减   (np.tile(a,(2,1))就是把a先沿x轴复制1倍，即没有复制，仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))
        squaredDiff = diff ** 2  # 平方
        squaredDist = np.sum(squaredDiff, axis=1)  # 和  (axis=1表示行)
        distance = squaredDist ** 0.5  # 开根号
        clalist.append(distance)
    clalist = np.array(clalist)  # 返回一个每个点到质点的距离len(dateSet)*k的数组
    return clalist


# 计算质心
def classify(dataSet, centroids, k):
    # 计算样本到质心的距离
    clalist = calcDis(dataSet, centroids, k)
    # 分组并计算新的质心
    minDistIndices = np.argmin(clalist, axis=1)  # axis=1 表示求出每行的最小值的下标
    newCentroids = pd.DataFrame(dataSet).groupby(
        minDistIndices).mean()  # DataFramte(dataSet)对DataSet分组，groupby(min)按照min进行统计分类，mean()对分类结果求均值
    newCentroids = newCentroids.values

    # 计算变化量
    changed = newCentroids - centroids

    return changed, newCentroids


# 使用k-means分类
def kmeans(dataSet, k):
    # 随机取质心
    centroids = random.sample(dataSet, k)

    # 更新质心 直到变化量全为0
    changed, newCentroids = classify(dataSet, centroids, k)
    while np.any(changed != 0):
        changed, newCentroids = classify(dataSet, newCentroids, k)

    centroids = sorted(newCentroids.tolist())  # tolist()将矩阵转换成列表 sorted()排序

    # 根据质心计算每个集群
    cluster = []
    clalist = calcDis(dataSet, centroids, k)  # 调用欧拉距离
    minDistIndices = np.argmin(clalist, axis=1)
    for i in range(k):
        cluster.append([])
    for i, j in enumerate(minDistIndices):  # enymerate()可同时遍历索引和遍历元素
        cluster[j].append(dataSet[i])

    return centroids, cluster


# 创建数据集
def createDataSet():
    return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]


if __name__ == '__main__':
    dataset = createDataSet()
    centroids, cluster = kmeans(dataset, 2)
    #print("数据集为：%s"%dataset)
    print('质心为：%s' % centroids)
    print('集群为：%s' % cluster)
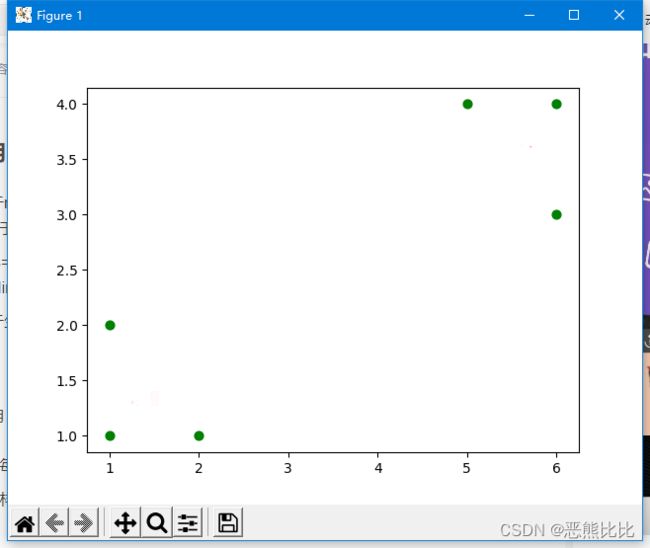
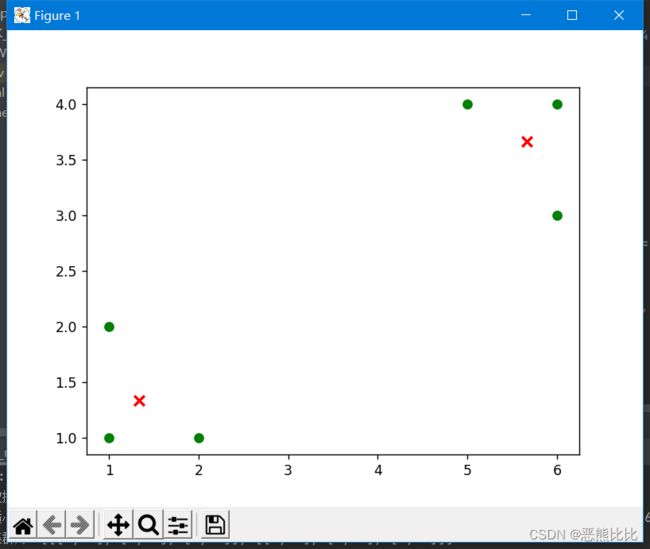
    for i in range(len(dataset)):
        plt.scatter(dataset[i][0], dataset[i][1], marker='o', color='green', s=40, label='原始点')
        #  记号形状       颜色      点的大小      设置标签
        for j in range(len(centroids)):
            plt.scatter(centroids[j][0], centroids[j][1], marker='x', color='red', s=50, label='质心')
            #plt.show()
    plt.show()

E:\PythonStudy\venv\Scripts\python.exe E:/PythonStudy/DeepLeraring/K_means_demo.py
质心为：[[1.3333333333333333, 1.3333333333333333], [5.666666666666667, 3.6666666666666665]]
集群为：[[[1, 1], [1, 2], [2, 1]], [[6, 4], [6, 3], [5, 4]]]

Process finished with exit code 0

//绿色表示数据集对应的散点
//红色叉号表示簇新