机器学习之隐马尔可夫模型(HMM)、最大熵马尔可夫模型(MEMM)、条件随机场(CRF)
导读
本次介绍的是三种机器学习模型,分别是隐马尔可夫HMM模型、最大熵马尔可夫模型以及条件随机场CRF模型,他们三个是一脉相承的,下面分别介绍
1.隐马尔科夫模型
隐马尔可夫模型(Hidden Markov Model)应用范围较广,主要应用在NLP序列标注问题上。例如分词、词性标注POS、命名实体识别NER等
它是经典的生成模型,学习的是联合概率矩阵 p ( x , y ) p(x,y) p(x,y),它是一个有向图模型,结构如下:
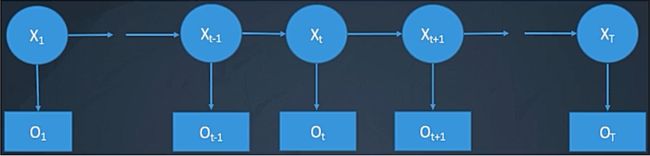
模型表示
五元组:(S,V, π \pi π,A,B),其中
S:隐藏状态集合,S = { s 1 s_{1} s1, s 2 s_{2} s2, … \dots …, s N s_{N} sN},即上图中X一共有几类。
V:观测状态集合,V = { ν 1 \nu_{1} ν1, ν 2 \nu_{2} ν2, … \dots …, ν N \nu_{N} νN},即上图中X一共有几类。
π \pi π:初始状态的概率, π \pi π={ π 1 \pi_{1} π1, π 2 \pi_{2} π2, … \dots …, π N \pi_{N} πN}; π i \pi_{i} πi = P( X 1 X_{1} X1 = s i s_{i} si)
A:状态转移概率矩阵,A = { a i j a_{ij} aij}; a i j a_{ij} aij = P( X t + 1 X_{t+1} Xt+1 = s j s_{j} sj| X t X_{t} Xt = s i s_{i} si),即由 s i s_{i} si转移到 s j s_{j} sj的概率}
B:符号输出概率,B = { b j k b_{jk} bjk};j ∈ \in ∈ S,k ∈ \in ∈ V
序列
状态序列: X = X 1 , X 2 , … , X T X = X_{1},X_{2},\dots,X_{T} X=X1,X2,…,XT \qquad X t ∈ S X_{t} \in S Xt∈S
输出序列: O = O 1 , O 2 , … , O T O = O_{1},O_{2},\dots,O_{T} O=O1,O2,…,OT \qquad O t ∈ V O_{t} \in V Ot∈V
一个随机过程,有一个观察序列 O = O 1 , O 2 , . . . , O T O = O_{1},O_{2},...,O_{T} O=O1,O2,...,OT,该过程隐含着一个状态序列 X = X 1 , X 2 , . . . , X T X = X_{1},X_{2},...,X_{T} X=X1,X2,...,XT
1.马尔科夫假设:
- 假设1:有限历史假设: P ( X i ∣ X 1 , X 2 , … , X T ) = P ( X i ∣ X i − 1 ) P(X_{i}|X_{1},X_{2},\dots,X_{T}) = P(X_{i}|X_{i-1}) P(Xi∣X1,X2,…,XT)=P(Xi∣Xi−1),即当前的隐含状态只与前一个有关,再之前的状态不对当前隐含状态起作用。
- 假设2:时间不动性假设
2.输出独立性假设
- 输出仅与当前状态有关: P ( O 1 , O 2 , … , O T ∣ X 1 , X 2 , … , X T ) = Π t P ( O t ∣ X t ) P(O_{1},O_{2},\dots,O_{T}|X_{1},X_{2},\dots,X_{T}) = \Pi_{t}P(O_{t}|X_{t}) P(O1,O2,…,OT∣X1,X2,…,XT)=ΠtP(Ot∣Xt)
HMM的三个基本问题
给定一个观察序列 O 1 , O 2 , … , O T O_{1},O_{2},\dots,O_{T} O1,O2,…,OT和模型 μ = ( A , B , π ) \mu = (A,B,\pi) μ=(A,B,π)
问题1:
如何有效计算观察序列 O 1 , O 2 , … , O T O_{1},O_{2},\dots,O_{T} O1,O2,…,OT的概率 P ( O ∣ μ ) P(O|\mu) P(O∣μ)? ⇒ \Rightarrow ⇒评价问题
问题2:
如何寻找最佳的状态序列 X 1 , X 2 , … , X T X_{1},X_{2},\dots,X_{T} X1,X2,…,XT? ⇒ \Rightarrow ⇒解码问题
问题3:
如何训练模型参数 μ = ( A , B , π ) \mu = (A,B,\pi) μ=(A,B,π),使得 P ( O ∣ μ ) P(O|\mu) P(O∣μ)概率最大? ⇒ \Rightarrow ⇒模型参数学习、训练问题
评价问题
P ( O ∣ μ ) = ∑ x P ( O , X ∣ μ ) = ∑ x P ( O ∣ X , μ ) P ( X ∣ μ ) P(O|\mu) = \sum_{x} P(O,X|\mu) = \sum_{x} P(O|X,\mu)P(X|\mu) P(O∣μ)=x∑P(O,X∣μ)=x∑P(O∣X,μ)P(X∣μ)
其中第一个等号为把X放到概率中,求和还是等于1,是不变的。然后利用概率公式拆开,即第二个等号。
第一项为:
P ( O ∣ X , μ ) = P ( O 1 , O 2 , … , O T ∣ X 1 , X 2 , … , X T , μ ) = ∏ i = 1 N P ( o i ∣ x i ) P(O|X,\mu) = P(O_{1},O_{2},\dots,O_{T}|X_{1},X_{2},\dots,X_{T},\mu) = \prod_{i=1}^{N}P(o_{i}|x_{i}) P(O∣X,μ)=P(O1,O2,…,OT∣X1,X2,…,XT,μ)=i=1∏NP(oi∣xi)
即观测概率,是已知的
第二项为:
P ( X ∣ μ ) = P ( X 1 , X 2 , … , X T ∣ μ ) = P ( x 1 ) ⋅ ∏ i = 2 N P ( x i ∣ x i − 1 ) P(X|\mu) = P(X_{1},X_{2},\dots,X_{T}|\mu) = P(x_{1}) \cdot \prod_{i=2}^{N}P(x_{i}|x_{i-1}) P(X∣μ)=P(X1,X2,…,XT∣μ)=P(x1)⋅i=2∏NP(xi∣xi−1)
即转移概率,也是已知的
解码问题
即如何寻找最佳的状态序列 X 1 , X 2 , … , X T X_{1},X_{2},\dots,X_{T} X1,X2,…,XT
X = a r g m a x P ( X ∣ O , μ ) = a r g m a x P ( O , X ∣ μ ) X = argmax P(X|O,\mu) = argmax P(O,X|\mu) X=argmaxP(X∣O,μ)=argmaxP(O,X∣μ)
解决该问题的方法是Viterbi算法,核心思想是动态规划
训练问题(有标注数据)
Baum-Welch算法
总结
HMM是生成式有向图模型,优势是训练和推断计算量较小,劣势是独立性假设严格,生成式模型,需要对联合概率建模
2.最大熵隐马尔科夫模型
最大熵隐马尔科夫模型(Maximum Entropy Markov Models,简称MEMM)是一个判别模型,形状见下图:

该模型求条件概率,公式如下:
P ( y 1 : n ∣ x 1 : n ) = ∏ i = 1 n P ( y i ∣ y i − 1 , x 1 : n ) = ∏ i = 1 n e x p ( w T f ( y i , y i − 1 , x 1 : n ) ) Z ( y i − 1 , x 1 : n ) P(y_{1:n}|x_{1:n}) = \prod_{i=1}^{n}P(y_{i}|y_{i-1},x_{1:n}) = \prod_{i=1}^{n} \frac{exp(w^{T}f(y_{i},y_{i-1},x_{1:n}))}{Z(y_{i-1},x_{1:n})} P(y1:n∣x1:n)=i=1∏nP(yi∣yi−1,x1:n)=i=1∏nZ(yi−1,x1:n)exp(wTf(yi,yi−1,x1:n))
与隐马尔可夫模型不同的是,现在是给定X的分布,算Y的分布
存在的问题
MEMM存在的最大问题即标签偏置(Labeling Bias)问题,原因是局部归一化导致。
3.条件随机场
传统的序列标注问题最有名的还是条件随机场(Conditional Random Fields,简称CRF)
性质
为判别模型,是一个无向图模型,使用了全局归一化,避免了MEMM的标签偏置问题
公式为:
P ( y ˉ ∣ x ˉ ; ω ) = e x p ( ∑ i ∑ j ω j f j ( y i − 1 , y i , x ˉ , i ) ) ∑ y ′ ∈ Y e x p ( ∑ i ∑ j ω j f j ( y i − 1 ′ , y i ′ , x ˉ , i ) ) P(\bar{y}|\bar{x};\omega) = \frac{exp(\sum_{i}\sum_{j}\omega_{j}f_{j}(y_{i-1},y_{i},\bar{x},i))}{\sum_{y^{\prime}\in Y}exp(\sum_{i}\sum_{j}\omega_{j}f_{j}(y^{\prime}_{i-1},y^{\prime}_{i},\bar{x},i))} P(yˉ∣xˉ;ω)=∑y′∈Yexp(∑i∑jωjfj(yi−1′,yi′,xˉ,i))exp(∑i∑jωjfj(yi−1,yi,xˉ,i))
优点与缺点
- 没有严格的独立性假设条件,可以容纳任意上下文信息;特征设计灵活
- 训练代价大