信号的相关分析(自相关和互相关) | python代码实战
信号的相关分析(自相关和互相关)
- 一、自相关函数
-
- (1) 自相关函数的定义
- (2) 自相关函数的性质
- (3) 自相关函数的计算
- 二、互相关函数
-
- (1) 互相关函数的定义
- (2) 互相关函数的性质
- 三、相关分析的应用
-
- (1) 自相关函数的应用
- (2) 互相关函数的应用
- 四、python代码实战
-
- 4.1 自相关代码实战
-
- 4.1.1 导入包
- 4.1.2 绘制不同信号的自相关信号
- 4.1.3 自相关代码分析
- 4.2互相关代码实战
-
- 4.2.1 同频率正弦余弦信号的互相关信号
- 4.2.2 不同频率信号之间的互相关信号
- 4.2.3 正弦与噪声之间的互相关信号
- 五、结论
欢迎关注公众号《故障诊断与python学习》
代码位置:https://github.com/HappyBoy-cmd/fault_diagnosis_signal_processing
参考资料:
书籍:机械故障诊断及典型案例解析(第2版,时献江)
Python信号处理:自相关函数(对标MATLAB中的autocorr)
一、自相关函数
(1) 自相关函数的定义
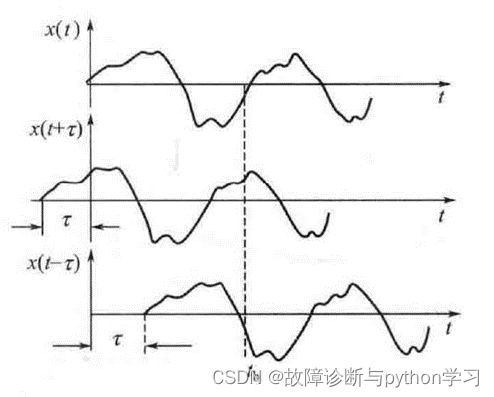
已知时间函数 x ( t ) {x(t)} x(t),其自相关函数 R x ( τ ) {R_{x}(\tau)} Rx(τ)的定义为:
R x ( τ ) = lim T → ∞ 1 T ∫ 0 T x ( t ) x ( t + τ ) d t {R_{x}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t) x(t+\tau) \mathrm{d} t} Rx(τ)=limT→∞T1∫0Tx(t)x(t+τ)dt
R x ( τ ) {R_{x}(\tau)} Rx(τ)主要用来描述 x ( t ) {x(t)} x(t)与其自身延时 τ {\tau} τ时刻之后的 x ( t + τ ) {x(t+\tau)} x(t+τ)相似程度,相似程度越高,相关值越大。 R x ( τ ) {R_{x}(\tau)} Rx(τ)的计算原理如图3.9 所示。
(2) 自相关函数的性质
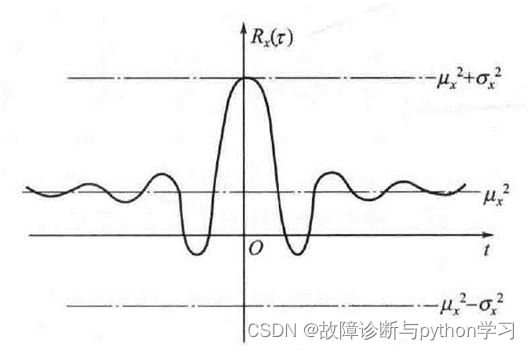
① R x ( τ ) {R_{x}(\tau)} Rx(τ)为实偶函数,即 R x ( τ ) = R x ( − τ ) {R_{x}(\tau)=R_{x}(-\tau)} Rx(τ)=Rx(−τ) 。
② 当 τ = 0 \tau=0 τ=0时, R x ( τ ) {R_{x}(\tau)} Rx(τ)的值最大,即 R x ( 0 ) ⩾ R x ( τ ) R_{x}(0) \geqslant R_{x}(\tau) Rx(0)⩾Rx(τ), 并等于信号的均方值 Ψ x 2 {\Psi_{x}^{2}} Ψx2。
R x ( 0 ) = lim 1 T ∫ 0 T x ( t ) x ( t + 0 ) d t = lim 1 T ∫ 0 T x 2 ( t ) d t = Ψ x 2 {R_{x}(0)=\lim \frac{1}{T} \int_{0}^{T} x(t) x(t+0) \mathrm{d} t=\lim \frac{1}{T} \int_{0}^{T} x^{2}(t) \mathrm{d} t=\Psi_{x}^{2}} Rx(0)=limT1∫0Tx(t)x(t+0)dt=limT1∫0Tx2(t)dt=Ψx2
③ 当 τ → ∞ {\tau \rightarrow \infty} τ→∞时,可认为 x ( t ) {x(t)} x(t)和 x ( t + τ ) {x(t+\tau)} x(t+τ)之间无关,即:
R x ( τ → ∞ ) → μ x 2 {R_{x}(\tau \rightarrow \infty) \rightarrow \mu_{x}^{2}} Rx(τ→∞)→μx2
若 x ( t ) {x(t)} x(t)的均值为0, 则 R x ( τ → ∞ ) → 0 {R_{x}(\tau \rightarrow \infty) \rightarrow 0} Rx(τ→∞)→0。
性质② 和③ 的图像如图3.10 所示。
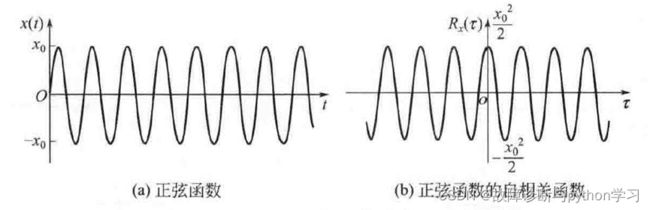
④ 周期函数的自相关函数仍是同频率的周期函数。假设正弦函数 x ( t ) = x 0 sin ( ω t + φ ) {x(t)=x_{0} \sin (\omega t+\varphi)} x(t)=x0sin(ωt+φ)的初始相位 φ {\varphi} φ是一个随机变量,根据自相关函数的定义,可求的自相关函数为:
R x ( τ ) = x 0 2 2 cos ω τ {R_{x}(\tau)=\frac{x_{0}^{2}}{2} \cos \omega \tau} Rx(τ)=2x02cosωτ
可见正弦函数的自相关函数是一个余弦函数,如图3.11所示。在 τ = 0 \tau=0 τ=0时具有最大值式 x 0 2 / 2 {x_{0}^{2} / 2} x02/2它保留了变量 x ( t ) {x(t)} x(t)的幅值信息 x 0 {x_{0}} x0和频率 ω { \omega} ω信息,但丢掉了初始相位 φ {\varphi} φ信息。
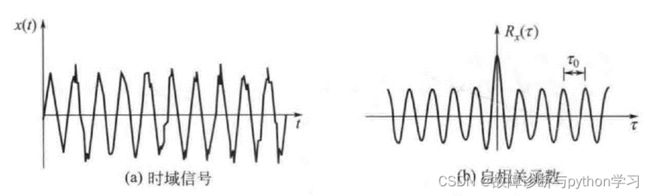
自相关函数主要用于检测混淆在随机信号中的周期信号成分,因为周期信号的自相关函数会按原频率重复出现,而随机信号在时间位移 τ {\tau} τ稍大时,由于自身的相乘消除作用,自相关函数很快趋于零( 假设均值 μ x = 0 {\mu_{x}=0} μx=0 ) ,如图3.12 所示。
设测得信号 y ( t ) = x ( t ) + n ( t ) {y(t)=x(t)+n(t)} y(t)=x(t)+n(t),其中 x ( t ) {x(t)} x(t)为正弦信号, n ( t ) {n(t)} n(t)为噪声, x ( t ) {x(t)} x(t)与 n ( t ) {n(t)} n(t)相互独立,则有:
R y ( τ ) = R x ( τ ) + R n ( τ ) R_{y}(\tau)=R_{x}(\tau)+R_{n}(\tau) Ry(τ)=Rx(τ)+Rn(τ)
当 τ {\tau} τ很大时, R n ( τ ) → 0 {R_{n}(\tau) \rightarrow 0} Rn(τ)→0 , 因此:
lim τ → ∞ R y ( τ ) R x ( τ ) = 1 {\lim _{\tau \rightarrow \infty} \frac{R_{y}(\tau)}{R_{x}(\tau)}=1} limτ→∞Rx(τ)Ry(τ)=1
即当 τ {\tau} τ大到一定程度时, y ( t ) {y(t)} y(t)与 x ( t ) {x(t)} x(t)完全相关。
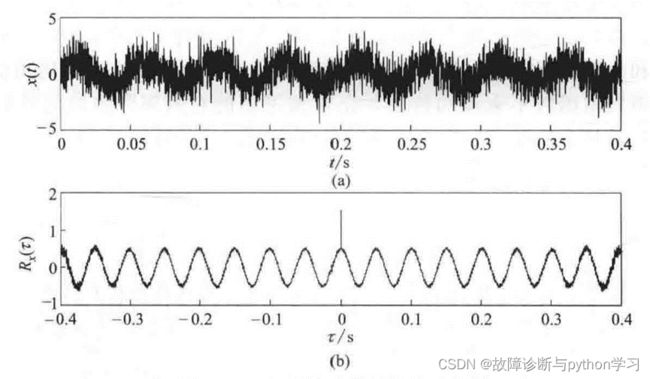
实际工程信号多数是随机噪声和确定性周期信号的混合体,如图3.13 所示。一般情况下.周期信号和故障特征有关,随机噪声对诊断无用。此时,可以利用随机信号的自相关函数迅速衰减,而周期函数不衰减的特性。在自相关图的右侧部分测取信号的周期,也就是说,自相关函数是从干扰噪声中找出周期信号或瞬时信号的重要手段. 延长变量 τ {\tau} τ的取值,就可将信号中的周期分量 τ 0 {\tau_0} τ0暴露出来。
(3) 自相关函数的计算
由于采样点数的限制,按照式(3.31)进行自相关函数的计算是不可能的,因为我们只能得到有限的样本曲线及有限的数据长度。对于连续的模拟信号 x ( t ) {x(t)} x(t),如测量时间长度为 , 则其自相关函数可按下式计算:
R ^ x ( τ ) = 1 T − τ ∫ 0 T − τ x ( t ) x ( t + τ ) d t ( 0 ⩽ t ⩽ T ) {\hat{R}_{x}(\tau)=\frac{1}{T-\tau} \int_{0}^{T-\tau} x(t) x(t+\tau) \mathrm{d} t \quad(0 \leqslant t \leqslant T)} R^x(τ)=T−τ1∫0T−τx(t)x(t+τ)dt(0⩽t⩽T)
式中, R ^ x ( τ ) {\hat{R}_{x}(\tau)} R^x(τ) 表示 R x ( τ ) {R_{x}(\tau)} Rx(τ)的估计值。 时延 τ \tau τ一定要远小于 T T T, 以保证测量精度。
对于从连续信号采样所得的离散的数字信号 x ( n ) , n = 1 , 2 , ⋯ , N {x(n), n=1,2, \cdots, N} x(n),n=1,2,⋯,N,其自相关函数可按下式估算:
R ^ x ( k ) = 1 N − k ∑ n = 1 N − k x ( n ) ( n + k ) k = 0 , 1 , 2 , ⋯ , M ; M ≪ N \hat{R}_{x}(k)=\frac{1}{N-k} \sum_{n=1}^{N-k} x(n)(n+k) \quad k=0,1,2, \cdots, M ; \quad M \ll N R^x(k)=N−k1∑n=1N−kx(n)(n+k)k=0,1,2,⋯,M;M≪N
为了保证测量精度,同样要使最大计算时延量 M M M远远小于数据点数 N N N, 以上可由计算机实现,称为直接计算法。因其计算量很大。近代的信号分析中已不采用这种方法。而是利用自相关函数与功率谱密度函数的关系,采用快速傅里叶变换算法实现,这部分内容将在后续介绍。
二、互相关函数
(1) 互相关函数的定义
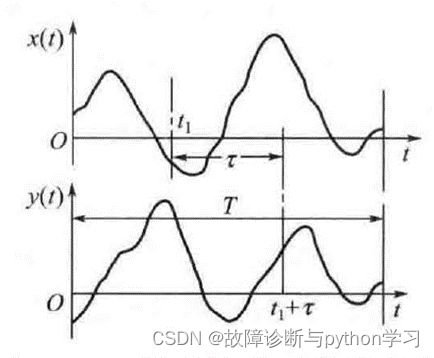
已知两个不同的信号 x ( t ) {x(t)} x(t)和 y ( t ) {y(t)} y(t), x ( t ) {x(t)} x(t)和 y ( t ) {y(t)} y(t)的互相关函数 R x y ( τ ) R_{x y}(\tau) Rxy(τ)定义为:
R x y ( τ ) = lim T → ∞ 1 T ∫ 0 T x ( t ) y ( t + τ ) d t R_{x y}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t) y(t+\tau) \mathrm{d} t Rxy(τ)=limT→∞T1∫0Tx(t)y(t+τ)dt
互相关函数用于评价两个信号之间的相似程度,其计算原理如图3.15 所示。
(2) 互相关函数的性质
① 互相关函数是非奇、非偶函数, 即 R x y ( τ ) = R y x ( − τ ) R_{x y}(\tau)=R_{y x}(-\tau) Rxy(τ)=Ryx(−τ)。
② ∣ R x y ( τ ) ∣ ⩽ R x x ( 0 ) R y y ( 0 ) \left|R_{x y}(\tau)\right| \leqslant \sqrt{R_{x x}(0) R_{y y}(0)} ∣Rxy(τ)∣⩽Rxx(0)Ryy(0),即 R x y ( 0 ) R_{x y}(0) Rxy(0) 一般不是最大值, R x y ( τ ) R_{x y}(\tau) Rxy(τ)的峰值不在 τ = 0 \tau=0 τ=0处。 R x y ( τ ) R_{x y}(\tau) Rxy(τ)的峰值偏离原点的位置 τ 0 \tau_{0} τ0反映了两信号时移的大小,此时两信号的相关程度最高,如图3.16 所示。
例如,当 x ( t ) = x 0 sin ( ω t + θ ) x(t)=x_{0} \sin (\omega t+\theta) x(t)=x0sin(ωt+θ), y ( t ) = y 0 sin ( ω t + θ + φ ) y(t)=y{0} \sin (\omega t+\theta+\varphi) y(t)=y0sin(ωt+θ+φ) 时, 其互相关函数 R x y ( τ ) R_{x y}(\tau) Rxy(τ)为:
R x y ( τ ) = lim T → ∞ 1 T ∫ 0 T x ( t ) y ( t + τ ) d t = 1 T 0 ∫ 0 T 0 x 0 y 0 sin ( ω t + θ ) sin [ ω ( t + τ ) + θ − φ ] d t = x 0 y 0 2 cos ( ω τ − φ ) \begin{array}{l} R_{x y}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t) y(t+\tau) \mathrm{d} t \\ =\frac{1}{T_{0}} \int_{0}^{T_{0}} x_{0} y_{0} \sin (\omega t+\theta) \sin [\omega(t+\tau)+\theta-\varphi] \mathrm{d} t \\ =\frac{x_{0} y_{0}}{2} \cos (\omega \tau-\varphi) \end{array} Rxy(τ)=limT→∞T1∫0Tx(t)y(t+τ)dt=T01∫0T0x0y0sin(ωt+θ)sin[ω(t+τ)+θ−φ]dt=2x0y0cos(ωτ−φ)
由此可见,在 τ = φ / ω = τ 0 \tau=\varphi / \omega=\tau_{0} τ=φ/ω=τ0处, R x y ( τ ) R_{x y}(\tau) Rxy(τ)取得最大值,表明两个信号此时最相关,因为 y ( t ) y(t) y(t)延时 y ( t ) y(t) y(t)时刻后与 x ( t ) x(t) x(t)最相近。与自相关函数不同,两个同频率的谐波信号的互相关函数不仅保留了两个信号的幅值 x 0 x_{0} x0, y 0 y_{0} y0信息、频率 ω \omega ω信息,而且还保留了两信号的相位差( 此处为 φ \varphi φ)信息。
③ 两个统计独立的随机信号, 当均值为零时,则 R x y ( τ ) = 0 R_{x y}(\tau)=0 Rxy(τ)=0。
④ 两个不同频率的周期信号互不相关,即互相关函数为零。假设对两个不同频率的简谐波信号:
x ( t ) = A 0 sin ( ω 1 t + θ ) , y ( t ) = B 0 sin ( ω 2 t + θ + φ ) x(t)=A_{0} \sin \left(\omega_{1} t+\theta\right), \quad y(t)=B_{0} \sin \left(\omega_{2} t+\theta+\varphi\right) x(t)=A0sin(ω1t+θ),y(t)=B0sin(ω2t+θ+φ)
进行相关分析,则:
R x y ( τ ) = lim T → ∞ 1 T ∫ 0 T 0 x ( t ) y ( t + τ ) d t = 1 T 0 ∫ 0 T 0 A 0 B 0 sin ( ω 1 t + θ ) sin [ ω 2 ( t + τ ) + θ − φ ] d t = A 0 B 0 2 T 0 ∫ 0 T 0 { cos [ ( ω 2 − ω 1 ) t + ( ω 2 τ − φ ) ] − cos [ ( ω 2 + ω 1 ) t + ( ω 2 τ + 2 θ − φ ) ] } d t = 0 \begin{array}{l} R_{x y}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T_{0}} x(t) y(t+\tau) \mathrm{d} t \\ =\frac{1}{T_{0}} \int_{0}^{T_{0}} A_{0} B_{0} \sin \left(\omega_{1} t+\theta\right) \sin \left[\omega_{2}(t+\tau)+\theta-\varphi\right] \mathrm{d} t \\ =\frac{A_{0} B_{0}}{2 T_{0}} \int_{0}^{T_{0}}\left\{\cos \left[\left(\omega_{2}-\omega_{1}\right) t+\left(\omega_{2} \tau-\varphi\right)\right]-\cos \left[\left(\omega_{2}+\omega_{1}\right) t+\left(\omega_{2} \tau+2 \theta-\varphi\right)\right]\right\} \mathrm{d} t \\ =0 \end{array} Rxy(τ)=limT→∞T1∫0T0x(t)y(t+τ)dt=T01∫0T0A0B0sin(ω1t+θ)sin[ω2(t+τ)+θ−φ]dt=2T0A0B0∫0T0{cos[(ω2−ω1)t+(ω2τ−φ)]−cos[(ω2+ω1)t+(ω2τ+2θ−φ)]}dt=0
即 R x y ( τ ) = 0 R_{x y}(\tau)=0 Rxy(τ)=0 。
⑤ 周期信号与随机信号的互相关函数为零。由于随机信号 y ( t + τ ) y(t+\tau) y(t+τ)在时间 t → t + τ t \rightarrow t+\tau t→t+τ内并无确定的关系,它的取值显然与任何周期函数 x ( t ) x(t) x(t)无关,因此 R x y ( τ ) = 0 R_{x y}(\tau)=0 Rxy(τ)=0 。
三、相关分析的应用
(1) 自相关函数的应用
用轮廓仪测得一机械加工表面的粗糙度信号 a ( t ) a(t) a(t),并进行自相关分析,得到自相关函数 R a ( τ ) R_{a}(\tau) Ra(τ),如图3.17 所示。根据 R a ( τ ) R_{a}(\tau) Ra(τ)就可以判断造成机械加工表面的粗糙度的原因。
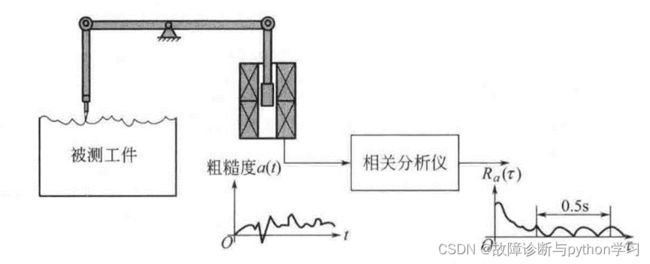
观察 a ( t ) a(t) a(t)的自相关函数 R a ( τ ) R_{a}(\tau) Ra(τ),发现其呈周期性,这说明造成粗糙度的原因之一是某种周期因素。从自相关函数图可以确定周期因素的频率为:
f = 1 T = 1 0.5 / 3 = 6 ( H z ) f=\frac{1}{T}=\frac{1}{0.5 / 3}=6(\mathrm{Hz}) f=T1=0.5/31=6(Hz)
根据加工该工件的机械设备中的各个运动部件的运动频率(如电动机的转速,拖板的往复运动次数,液压系统的油脉动频率等),通过测算和对比分析,运动频率与6Hz 接近的部件的振动,就应该是造成该粗糙度的主要原因。
(2) 互相关函数的应用
相关分析在机械设备故障诊断和振动控制中最直接的应用是传递问题,其中包括传递路径的识别和故障源的识别这两类问题。 间接的应用是相关测速和相关定位问题。
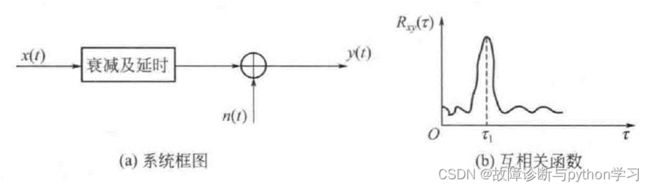
设时间信号(振动或噪声) x ( t ) x(t) x(t)通过一个非频变线性路径进行传递,传递过程中产生时延 τ 1 \tau_{1} τ1,并混入噪声 n ( t ) n(t) n(t)。 可以用图3.18 (a) 描述。若传递路径的衰减因子为常数 α \alpha α,则这个系统的输出 y ( t ) y(t) y(t)可表示为:
y ( t ) = α x ( t − τ 1 ) + n ( t ) y(t)=\alpha x\left(t-\tau_{1}\right)+n(t) y(t)=αx(t−τ1)+n(t)
计算输入与输出信号的互相关函数为:
R x y ( τ ) = lim T → ∞ 1 T ∫ 0 T x ( t ) y ( t + τ ) d t = lim T → ∞ 1 T ∫ 0 T x ( t ) [ α x ( t + τ − τ 1 ) + n ( t + τ ) ] d t = lim T → ∞ 1 T ∫ 0 T α x ( t ) x ( t + τ − τ 1 ) + lim T → ∞ 1 T ∫ 0 T x ( t ) n ( t + τ ) d t = R x ( τ − τ 1 ) + R x n ( τ ) = R x ( τ − τ 1 ) \begin{array}{l} R_{x y}(\tau)=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t) y(t+\tau) \mathrm{d} t \\ =\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t)\left[\alpha x\left(t+\tau-\tau_{1}\right)+n(t+\tau)\right] \mathrm{d} t \\ =\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} \alpha x(t) x\left(t+\tau-\tau_{1}\right)+\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} x(t) n(t+\tau) \mathrm{d} t \\ =R_{x}\left(\tau-\tau_{1}\right)+R_{x n}(\tau)=R_{x}\left(\tau-\tau_{1}\right) \end{array} Rxy(τ)=limT→∞T1∫0Tx(t)y(t+τ)dt=limT→∞T1∫0Tx(t)[αx(t+τ−τ1)+n(t+τ)]dt=limT→∞T1∫0Tαx(t)x(t+τ−τ1)+limT→∞T1∫0Tx(t)n(t+τ)dt=Rx(τ−τ1)+Rxn(τ)=Rx(τ−τ1)、
根据互相关的性质⑤ ,式中 R x n ( τ ) = 0 R_{x n}(\tau)=0 Rxn(τ)=0, 计算结果为 x ( t ) x(t) x(t)在 τ = τ 1 \tau=\tau_{1} τ=τ1的互相关函数,如图3.18(b)所示。该图表示 y ( t ) y(t) y(t)在延时 τ 1 \tau_{1} τ1时刻后与 x ( t ) x(t) x(t)相关.或者说 y ( t ) y(t) y(t)是延时 τ 1 \tau_{1} τ1时刻后,并且幅值衰减了的 x ( t ) x(t) x(t)。
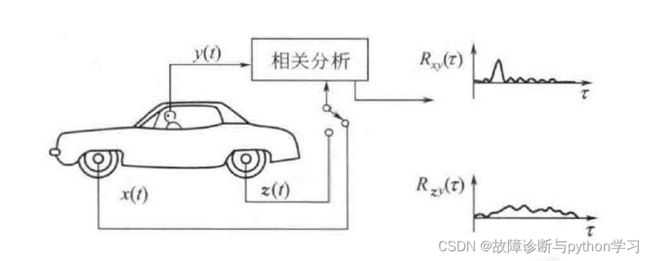
① 故障源检测图3.19 给出一个用互相关函数诊断汽车驾驶员座椅振动源的例子。座椅上的振动信号为 y ( t ) y(t) y(t),前轮轴梁和后轮轴架上的振动信号分别为 x ( t ) x(t) x(t)和 z ( t ) z(t) z(t),分别求 R x y ( τ ) R_{x y}(\tau) Rxy(τ)和 R z y ( τ ) R_{z y}(\tau) Rzy(τ)。从图上可看出 R x y ( τ ) R_{x y}(\tau) Rxy(τ)有突出的谱峰.说明座椅的振动 y ( t ) y(t) y(t)主要是由于前轮的振动 x ( t ) x(t) x(t)引起的。
② 相关定位用
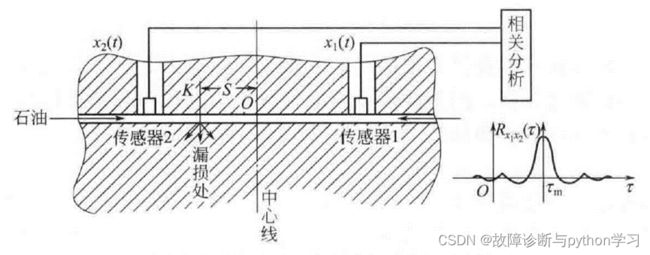
互相关分析法确定深埋地下的输油管裂损位置,如图3.20 所示。漏损处 K K K可视为向两侧传播声音的声源,在两侧管道上分别放置传感器1 和2 。因为放置传感器的两点相距漏损处距离不等, 则漏油的声响传至两传感器的时间就会有差异,在互相关函数图上 τ = τ m \tau=\tau_{\mathrm{m}} τ=τm处有最大值,这个 τ m \tau_{\mathrm{m}} τm就是时差,用 τ m \tau_{\mathrm{m}} τm就可以确定漏损处的位置。
假设 v v v为声音在管道中的传播速度,则漏损处 K K K 距中心点 O O O 的距离 S S S 为:
S = 1 2 v τ m S=\frac{1}{2} v \tau_{\mathrm{m}} S=21vτm
四、python代码实战
4.1 自相关代码实战
4.1.1 导入包
import scipy.io as scio
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal, fftpack, stats
import random
import os
import statsmodels.tsa.api as smt
import statsmodels
from matplotlib import rcParams
config = {
"font.family": 'serif', # 衬线字体
"font.size": 10, # 相当于小四大小
"font.serif": ['SimSun'], # 宋体
"mathtext.fontset": 'stix', # matplotlib渲染数学字体时使用的字体,和Times New Roman差别不大
'axes.unicode_minus': False # 处理负号,即-号
}
rcParams.update(config)
fs = 1000 # 采样频率1000Hz
f = 10 # 信号频率 10Hz
n = np.arange(0, 4096) # 生成4096点的序列
print(n)
>>>输出结果
[ 0 1 2 ... 4093 4094 4095]
t = n/fs # 生成4096点的时间序列
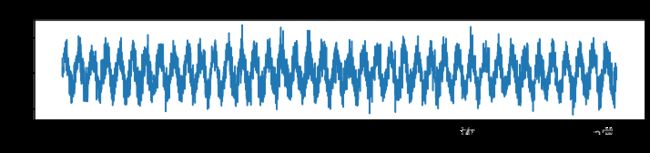
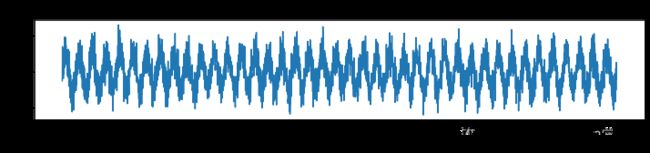
x = np.sin(2 * np.pi * n/fs * f) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize=(12,2))
plt.plot(x)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('正弦信号+噪声信号图')
plt.show()
print(x.shape)
>>>输出结果
(4096,)
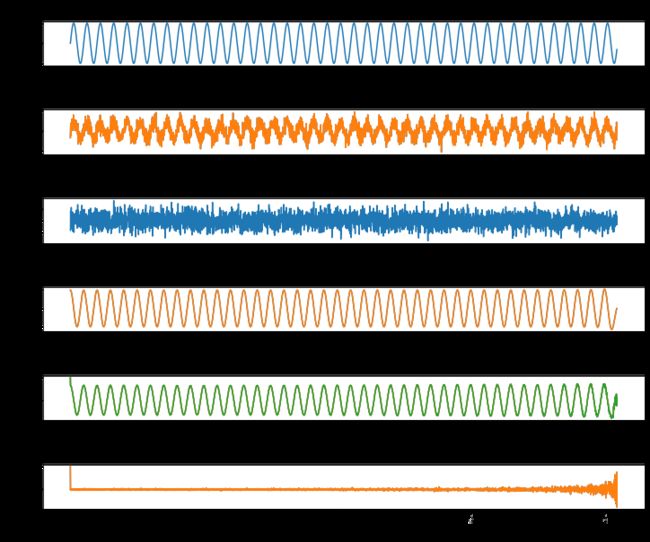
4.1.2 绘制不同信号的自相关信号
plt.figure(figsize=(12,10))
plt.subplots_adjust(wspace = 1, hspace = 1)
##===========绘制正弦信号图==========##
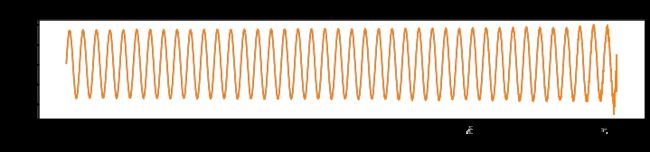
x1 = np.sin(2 * np.pi * n/fs * f)
plt.subplot(6, 1, 1)
plt.plot(t, x1)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('sin(2 * pi * t * f) 正弦信号图')
##===========绘制正弦信号+噪声图==========##
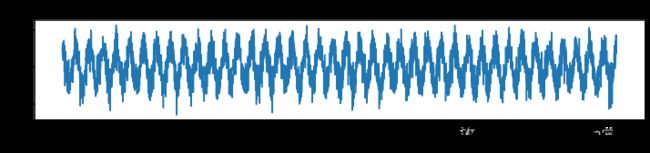
x2 = np.sin(2 * np.pi * n/fs * f) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.subplot(6, 1, 2)
plt.plot(t, x2)
plt.plot(t, x2)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('sin(2 * pi * t * f) 正弦信号+噪声图')
##===========绘制噪声信号图==========##
x3 = 0.5*np.random.randn(4096)
plt.subplot(6, 1, 3)
plt.plot(t, x3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('噪声信号图')
##===========绘制正弦信号的自相关信号图==========##
acf1 = np.correlate(x1, x1, mode='full')
N = len(x1)
acf1 = acf1[N-1:]
acf1 = acf1 / np.arange(N, 0, -1)
acf1 = acf1 / acf1[0]
plt.subplot(6, 1, 4)
plt.plot(t, acf1)
plt.plot(t, acf1)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('正弦信号的自相关信号图')
##===========绘制正弦信号+噪声的自相关信号图==========##
acf2 = np.correlate(x2, x2, mode='full')
N = len(x2)
acf2 = acf2[N-1:]
acf2 = acf2 / np.arange(N, 0, -1)
acf2 = acf2 / acf2[0]
plt.subplot(6, 1, 5)
plt.plot(t, acf2)
plt.plot(t, acf2)
plt.plot(t, acf2)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('正弦信号+噪声的自相关信号图')
##===========绘制噪声信号的自相关信号图=========##
x4 = 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
acf3 = np.correlate(x4, x4, mode='full')
N = len(x4)
acf3 = acf3[N-1:]
acf3 = acf3 / np.arange(N, 0, -1)
acf3 = acf3 / acf3[0]
plt.subplot(6, 1, 6)
plt.plot(t, acf3)
plt.plot(t, acf3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('噪声的自相关信号图')
4.1.3 自相关代码分析
x4 = np.sin(2 * np.pi * n/fs * f) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize=(12,6))
plt.subplots_adjust(wspace = 1, hspace = 1)
##===========绘制正弦信号自相关信号未处理图=========##
plt.subplot(3, 1, 1)
acf3 = np.correlate(x4, x4, mode='full')
plt.plot(acf3)
##===========绘制正弦信号自相关信号一半图==========##
plt.subplot(3, 1, 2)
N = len(x4)
acf3 = acf3[N-1:]
plt.plot(acf3)
##===========绘制正弦信号的自相关信号处理后图=========##
plt.subplot(3, 1, 3)
acf3 = acf3 / np.arange(N, 0, -1) # 用于消除时滞的影响 https://blog.csdn.net/qq_38290475/article/details/106992733
acf3 = acf3 / acf3[0]
plt.plot(acf3)
4.2互相关代码实战
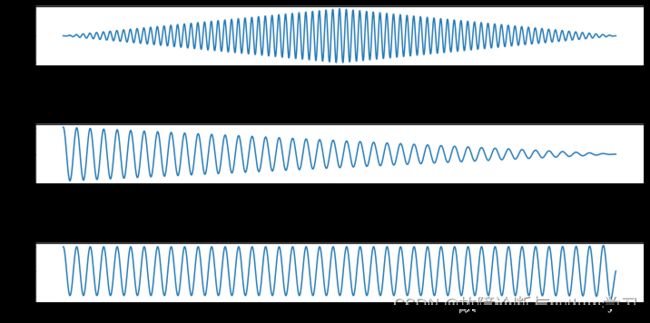
4.2.1 同频率正弦余弦信号的互相关信号
t = n/fs # 生成4096点的时间序列
f1 = 10
x1 = np.sin(2 * np.pi * n/fs * f1) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize = (12, 2))
plt.plot(x1)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('频率为10Hz正弦信号+噪声的时域图')
t = n/fs # 生成4096点的时间序列
f2 = 10
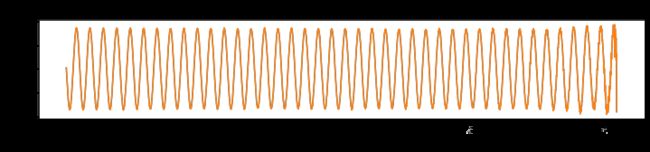
x2 = 1*np.cos(2 * np.pi * n/fs * f2) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize = (12, 2))
plt.plot(x2)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('频率为10Hz余弦信号+噪声的时域图')
acf3 = np.correlate(x1, x2, mode='full')
N = len(x1)
acf3 = acf3[N-1:]
acf3 = acf3 / np.arange(N, 0, -1)
acf3 = acf3 / acf3[0]
plt.figure(figsize = (12, 2))
plt.plot(t, acf3)
plt.plot(t, acf3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('同频率正弦余弦信号的自相关信号图(sin,cos)')
acf3 = np.correlate(x2, x1, mode='full')
N = len(x1)
acf3 = acf3[N-1:]
acf3 = acf3 / np.arange(N, 0, -1)
acf3 = acf3 / acf3[0]
plt.figure(figsize = (12, 2))
plt.plot(t, acf3)
plt.plot(t, acf3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('同频率正弦余弦信号的自相关信号图(cos,sin)')
4.2.2 不同频率信号之间的互相关信号
t = n/fs # 生成4096点的时间序列
f1 = 10
x1 = np.sin(2 * np.pi * n/fs * f1) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize = (12, 2))
plt.plot(x1)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('频率为10Hz的正弦信号+噪声信号的时域图')
t = n/fs # 生成4096点的时间序列
f2 = 15
x2 = np.cos(2 * np.pi * n/fs * f2) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize = (12, 2))
plt.plot(x2)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('频率为20Hz余弦信号+噪声信号的时域图')
acf3 = np.correlate(x1, x2, mode='full')
N = len(x1)
acf3 = acf3[N-1:]
acf3 = acf3 / np.arange(N, 0, -1)
acf3 = acf3 / acf3[0]
plt.figure(figsize = (12, 2))
plt.plot(t, acf3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('不同频率正弦和余弦信号的自相关信号图')
4.2.3 正弦与噪声之间的互相关信号
t = n/fs # 生成4096点的时间序列
f1 = 10
x1 = 0.5*np.random.randn(4096) # 生成随机信号
plt.figure(figsize = (12, 2))
plt.plot(x1)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('噪声信号的时域图')
x.shape
t = n/fs # 生成4096点的时间序列
f2 = 15
x2 = 1*np.cos(2 * np.pi * n/fs * f2) + 0.5*np.random.randn(4096) # 生成正弦信号 sin(2*pi*f*t) + 随机信号
plt.figure(figsize = (12, 2))
plt.plot(x2)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('余弦信号+噪声的时域图')
acf3 = np.correlate(x1, x2, mode='full')
N = len(x1)
acf3 = acf3[N-1:]
acf3 = acf3 / np.arange(N, 0, -1)
acf3 = acf3 / acf3[0]
plt.figure(figsize = (12, 2))
plt.plot(t, acf3)
plt.plot(t, acf3)
plt.xlabel('time(s)')
plt.ylabel('Amp(m/s2)')
plt.title('正弦信号与噪声的互相关信号图')
五、结论
自相关
- 周期信号做自相关可以滤去噪声
- 噪声信号做自相关结果趋于0
- 未知周期信号+噪声信号做自相关可以获取周期信号的周期
互相关
- 同频率周期信号做互相关可以获取相位差
- 不同频率周期信号做互相关结果趋于0
- 周期信号与噪声信号做互相关结果趋于0