nlp论文——《Efficient Estimation of Word Representations in Vector Space》(向量空间中词表示的有效估计)
目录
- 《Efficient Estimation of Word Representations in Vector Space》
- 第一课时:论文导读
-
- (1)语言模型
- (2)词向量简介——介绍词向量的概念和种类
- (3)前期知识储备
- 第二课时:论文精读(上)
-
- 1.论文整体框架
-
- 1.1 相关论文:
- 1.2 论文结构
- 2.神经网络语言模型
-
- 2.1 介绍改进前的NNLM网络模型
- 2.2 循环神经网络语言模型(RNNLM)
- 3.语言模型评价指标——困惑度(Perplexity)
-
- 3.1 语言模型困惑度与Loss关系
- 4.课时小结
- 第三课时:论文精读(下)
-
- Word2vec 原理
- 1.CBOW模型——介绍word2vec工具中的连续词袋模型
-
- 1.1 CBOW算法
- 1.2 Skip-gram算法 —— 跳字模型
- 2.Word2vec模型复杂度讨论
-
- 2.1 层次softmax
- 2.2 负采样
-
- 2.2.1 负采样原理
- 2.3 重采样(二次采样)
- 2.4 word2vec关键技术总结
- 3.模型复杂度
-
- 3.1 模型复杂度的概念
- 3.2 NNLM模型复杂度
- 3.3 RNNLM模型复杂度
- 3.4 Skip-Gram模型复杂度
- 3.5 CBOW模型复杂度
- 3.6 模型复杂度对比
- 4.实验和结果——介绍论文中的模型的实验设置和运行结果
- 5.讨论和结论
《Efficient Estimation of Word Representations in Vector Space》
- 作者:Tomas Mikolov, Kai Chen, Greg Corrade, Jeffrey Dean
- 单位:谷歌
- 论文来源:ICLR 2013
第一课时:论文导读
(1)语言模型
语言模型概念:语言模型是计算一个句子是句子的概率的模型;
在自然语言处理研究的早期,人们试图整理出关于自然语言处理的语法,并且根据这些语法去理解和生成句子。然而在现实生活中,自然语言总是过于复杂,人们为了方便沟通,使用的句子通常不拘泥于固定的语法,每个单词的含义在不同的语句下也有很多种变化。从20世纪80年代起,随着硬件计算机能力的增强和大型语料库的出现,使用统计方法对语言进行概率建模的方式开始变成主流。从2010年起,基于循环神经网络的方法在许多自然语言处理的问题上都超过了传统的统计模型,在学术和工业界都得到了广泛的应用。其中语言模型是自然语言处理问题中的一类最基本的问题,它有着非常广泛的应用,也是理解一些复杂的自然语言处理任务的基础。
我们所说的词向量Word2vector,它的本质其实也是一个语言模型,我们来看一下它为什么叫语言模型。我们熟知的自然语言处理非常热门的应用,比如说接触到的机器翻译、拼写纠错以及智能机器人,这些任务在做一些事情的时候都会涉及到语言模型,因为它们接触的都是一句一句的话,与我们之前所学习过的机器翻译的任务举例,神经网路在做机器翻译的时候,它会怎么做呢?
比如让机器翻译一下“我今天买了什么菜,它的价格很高”。那价格很高这个短语该怎么翻译呢?通常情况下,机器都会翻译成“high price”,而不会翻译成“large price”。因为机器会利用之前翻译过的一些东西学到一些信息,比如说学习到在形容价格高这个意思的时候,在之前的翻译中,“high”和“price”的组合在一起更多,而不是“large”与“price”组合。机器生成“high price”的概率就要大于“large price”的概率。这就是在机器翻译过程中我们会遇到的语言模型和概率的东西。
所以我们可以假设一门语言中所有可能的句子都服从某一个概率分布,每个句子出现的概率加起来为一,那么语言模型的任务就是预测每一个句子在语言中的概率。对于语言中常见的句子,一个好的语言模型应该得到相对高的概率,而对于不太合法的句子计算出的概率应该接近为零,语言模型仅仅是对句子出现的概率进行建模,并不会尝试去理解句子中的内容含义。比如我们说,语言模型能够告诉我们什么样的句子是常用的句子,但是却没有办法告诉我们两句话的意思是否相似或者相反。接下来我们就围绕这个概率值来说一说语言模型中的计算。
举例:我 今天 下午 打 羽毛球
P ( S ) = P ( w 1 , w 2 , . . . , w m ) P(S)=P(w_1,w_2,...,w_m) P(S)=P(w1,w2,...,wm)
= P ( w 1 ) ∗ P ( w 2 , . . . , w m ∣ w 1 ) =P(w_1)*P(w_2,...,w_m|w_1) =P(w1)∗P(w2,...,wm∣w1)
= P ( w 1 ) ∗ P ( w 2 ∣ w 1 ) ∗ P ( w 3 , . . . , w m ∣ w 1 , w 2 ) =P(w_1)*P(w_2|w_1)*P(w_3,...,w_m|w_1,w_2) =P(w1)∗P(w2∣w1)∗P(w3,...,wm∣w1,w2)
= P ( w 1 ) ∗ P ( w 2 ∣ w 1 ) ∗ P ( w 3 ∣ w 1 , w 2 ) , . . . , P ( w m ∣ w 1 , w 2 , . . , w m − 1 ) =P(w_1)*P(w_2|w_1)*P(w_3|w_1,w_2),...,P(w_m|w_1,w_2,..,w_{m-1}) =P(w1)∗P(w2∣w1)∗P(w3∣w1,w2),...,P(wm∣w1,w2,..,wm−1)
= P ( w 1 ) ∗ ∏ i = 2 m P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) =P(w_1)*\prod_{i=2}^{m} P(w_i|w_1,w_2,...,w_{i-1}) =P(w1)∗∏i=2mP(wi∣w1,w2,...,wi−1)
P(S)被称为语言模型,即用来计算一个句子概率的模型
这里先给大家说一下这样的一个事情。比如说现在我说了一句话:“我今天下午打羽毛球”。那当我在说这句话时大家可以想一下,这句话是什么都没想就完整地直接说出来吗?好像不是这样一回事,我在说这样的一句话的时候,通常情况下是一点一点思考之后再说的,不是说能够非常快地一瞬间就把它说完,而是经过了一个思考的瞬间。是先说了“我”,再说“今天”,“下午”,当说完这三个词的时候,其实大脑中就有一个潜意识,下句话要说什么,比如说今天下午想打羽毛球。经过一个这样的思考,我才说出了打羽毛球这样的句子,整个句子是边说边进行组织的。通过这样有逻辑的思考,我说完了这句话,而不是直接什么都不想,直接就说出来,这种情况下可能性不大,因为一般我们说什么话都要经过大脑的思考。
所以我们说的语言模型,比如我今天说了这句话,那这句话出现的概率多大呢?这里制定了一个 P ( s ) P(s) P(s),表示现在说的“我今天下午打羽毛球”,这句话出现的概率。我们可以想到这句话出现的概率是和每一个字相关的。于是可以写成下面的联合概率分布。更通俗地讲,我们在说一句话的时候,对于这样的联合概率分布,可以给他进行一个转换。比如说我第一个词说的是“我”,那对于一个完整的句子,它后边出现的概率是不是和第一个词出现的概率相关呢,这里用 P ( w 1 ) P(w_1) P(w1)来表示。后边是在说了“我”这个单词的基础上说了“今天”。这里我们要注意一点,“今天”这个单词并不是我直接说出来的单词,他是建立在前边说了“我”这个单词的基础上的。所以第二个单词 w 2 w_2 w2是一个建立在 w 1 w_1 w1上的条件概率 P ( w 2 ∣ w 1 ) P(w_2|w_1) P(w2∣w1)。
现在考虑第三个词“下午”,“下午”是在说了“我”和“今天”之后出现的,所以可以计算 w 3 w_3 w3出现的概率的形式为 P ( w 3 ∣ w 1 , w 2 ) P(w_3|w_1,w_2) P(w3∣w1,w2)。后面的句子可以按照这个逻辑以此类推,对于“羽毛球”来说,要先计算前面“我”,“今天”,“下午”,“打”这些单词出现的概率,之后根据前面这些词出现的概率再计算羽毛球这个单词出现的概率。也就是说语言模型就是计算一个句子出现概率的模型,这里通常把它转化成一种条件概率。也就是说每一个词的出现是和前面的出现有关系的。每一个词并不是独立的,是根据前面说的话把它们融合起来得到的。
那如何计算当前词 w i w_i wi在前边说过的词 w 1 w_1 w1, w 2 w_2 w2,一直到 w i − 1 w_{i-1} wi−1的条件概率P呢?最简单的方法就是直接做除法,先计算整句话在训练语料库中出现的次数,然后算一下在不算当前词 w i w_i wi后句子出现的次数。最终算一下这两个值的比值概率。具体的计算方式如下公式所示。
P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) = P ( w 1 , w 2 , . . . , w i ) / P ( w 1 , w 2 , . . . , w i − 1 ) P(w_i|w_1,w_2,...,w_{i-1})=P(w_1,w_2,...,w_i)/P(w_1,w_2,...,w_{i-1}) P(wi∣w1,w2,...,wi−1)=P(w1,w2,...,wi)/P(w1,w2,...,wi−1)
但是这样的计算的计算量特别大,会导致数据过于稀疏,因为每一个词都要考虑前面很多很多的词,而前面很多词组合在一起的概率其实并没有很高,组合到一起的词越多,它的数据模型是越稀疏的。因为数据非常稀疏,这会导致参数空间太大。
为了解决数据过于稀疏和参数空间太大的问题,提出了一种解决问题的思路。基于马尔科夫假设,提出下一个词的出现仅依赖于它前面的一个或几个词。
- 假设下一个词的出现依赖它前面的一个词,则有:
P ( S ) = P ( w 1 ) ∗ P ( w 2 ∣ w 1 ) ∗ P ( w 3 ∣ w 1 , w 2 ) . . . P ( w n ∣ w 1 , w 2 , . . . , w n − 1 ) P(S)=P(w_1)*P(w_2|w_1)*P(w_3|w_1,w_2)...P(w_n|w_1,w_2,...,w_{n-1}) P(S)=P(w1)∗P(w2∣w1)∗P(w3∣w1,w2)...P(wn∣w1,w2,...,wn−1)=P(w_1)*P(w_2|w_1)*P(w_3|w_2)…P(w_n|w_{n-1})$$
- 假设下一个词的出现依赖它前面的两个词,则有:
P ( S ) = P ( w 1 ) ∗ P ( w 2 ∣ w 1 ) ∗ P ( w 3 ∣ w 1 , w 2 ) . . . P ( w n ∣ w 1 , w 2 , . . . , w n − 1 ) P(S)=P(w_1)*P(w_2|w_1)*P(w_3|w_1,w_2)...P(w_n|w_1,w_2,...,w_{n-1}) P(S)=P(w1)∗P(w2∣w1)∗P(w3∣w1,w2)...P(wn∣w1,w2,...,wn−1)
= P ( w 1 ) ∗ P ( w 2 ∣ w 1 ) ∗ P ( w 3 ∣ w 1 , w 2 ) . . . P ( w n ∣ w n − 2 , w n − 1 ) =P(w_1)*P(w_2|w_1)*P(w_3|w_1,w_2)...P(w_n|w_{n-2},w_{n-1}) =P(w1)∗P(w2∣w1)∗P(w3∣w1,w2)...P(wn∣wn−2,wn−1)
在这样的假设下,计算的概率数据不会太稀疏,参数的数量也不会太大。所以在实际当中,我们并不制定一个句子中的一个词与它前面的每一个词都相关,而是只假设只与前面的一个或者几个词有关,通常把这个模型叫n-gram模型。
n-gram模型:假设当前词的出现概率只与它前面的N-1个词相关,意思就是指定n=1时,相当于只和它前面的一个词有关,当指定n=2时,相当于只和它前面的两个词相关。当n分别取值为1,2,3时,可以称之为unigram,bigram和trigram。
如何选择n
- 更大的n:对下一个词出现的约束信息更多,具有更大的辨别力;
- 更小的n:词语组成的短语在训练语料库中出现的次数更多,具有更可靠的统计信息,具有更高的可靠性。
- 理论上,n越大越好,经验上,trigram用的最多,尽管如此,原则上,能用bigram解决,绝不使用trigram。
n-gram模型的参数一般采用最大似然估计来进行计算,计算公式如下所示:
P ( w i ∣ w 1 , w 2 , w 3 , . . . , w i − 1 ) = C o u n t ( w 1 , w 2 , w 3 , . . . , w i − 1 , w i ) C o u n t ( w 1 , w 2 , w 3 , . . . , w i − 1 ) P(w_i|w_1,w_2,w_3,...,w_{i-1})=\frac{Count(w_1,w_2,w_3,...,w_{i-1},w_i)}{Count(w_1,w_2,w_3,...,w_{i-1})} P(wi∣w1,w2,w3,...,wi−1)=Count(w1,w2,w3,...,wi−1)Count(w1,w2,w3,...,wi−1,wi)Count(X):单词序列X在训练语料库中出现的次数。
训练语料库的规模越大,参数估计的结果就越可靠,但即使训练数据的规模非常大,还是有很多单词在训练语料库中是不会出现的,这就导致了很多参数为零。
举例来说,IBM使用了366M的英语语料训练了trigram,发现了有14.7%的trigram和2.2%的biggram在训练中没有办法出现,为了避免因为乘于零导致整个句子的概率都为零,在使用最大似然估计方法时需要加入平滑避免参数取值为零。
(2)词向量简介——介绍词向量的概念和种类
无论是一句话还是一篇文章,都是由一个个词组成的。这些词是我们可以利用的最基本的单位,为了能够让机器去利用这些词的信息,需要把这些词装换成数字信息,于是引入了词向量。词向量的意思是通过一个数字组成的向量来表示一个词,这个向量的构成可以有很多种,最简单的方式就是独热编码。
one-hot representation——独热编码
假设在一个语料集合中一共有n个不同的词,则可以使用一个长度为n的向量,对于第i个词来说,除了第i个位置的值为1,向量的其它位置的值都为0,这样就可以由唯一的一个,由1和0组成的向量表示一个词。
以上图为例,假设Rome这个单词为单词表里的第一个单词,那么就把第一个位置标成1,其余的位置都标为0;假设pairs为第二个单词,那就可以在第二个位置标为1,其余位置标为0;每一个向量的维度是单词表的长度。独热编码比较简单,也比较容易理解,但是存在很多问题,这种表示方法最大的一个问题就是没有办法捕捉词与词之间的相似度,这个也通常称为“语义鸿沟问题”;one-hot的基本假设是词与词之间的语义和语法都是相对独立的,仅仅从两个向量是无法看出两个词汇之间的关系的,这种独立性并不适合词汇的语义运算。同时,one-hot存在维度爆炸问题,随着字典的规模越来越大,模型的维度也会变得越来越大,矩阵也会变得越来越稀疏,这种维度的暴增会大大地消耗计算资源,并且我们也无法用这种one-hot表示来表示一些从未出现的词汇。因此在实际工程中,很少使用one-hot向量。
one-hot缺点
- 语义鸿沟问题
- 维数灾难、稀疏
- 无法表示未出现的词汇
由于one-hot存在的诸多问题,我们希望使用的这个向量不光能映射成一个数值,而且必须让这个数值是有意义的。所谓有意义,是指这个词语的向量不能只是一个数字,而是表示的向量必须有一层潜在的含义。
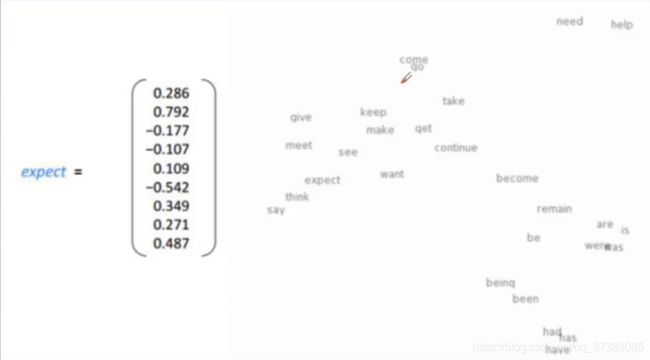
在上图中,expect对应的向量是由一些数值表示的,通常情况下,这些值是不大的,这个可以由我们指定,一般在-1到1之间,每个值都有正有负。对于向量可以指定一个维度,如果想要构造出更复杂的向量,就可以使向量的维度更大一些;如果想要构造出相对简单的向量,可以让维度稍微小一些。
对于一个语料库来说,每个词和每个词之间都是有一定距离的,比如上图中的一些单词,右下角有一个have,has,had,假设把这三个词分布到一个向量空间的模型中,空间是2维的,对于这两个维度来说,可以看到向量表达的意思是将近的。既然词之间的含义差不多,那么向量之间的位置也是相近的,所以对词向量要有这样一种生成规律:生成的向量不能是杂乱无序的,必须让向量有一层潜在的含义,这里用到了词向量的分布式表示。
分布式表示最早在1986年提出的,它的基本思想是通过训练将每个值映射成为k维的实数向量,通过词与词之间的距离,比如余弦相似度、欧式距离等等,来判断词与词之间的语义相似度。
本篇论文所要讲的word2vec使用的就是这种分布式表示的词向量表示方式。

可以通过词向量来做一些事情,如果想看一下什么词和frogs青蛙是最接近的,就可以在刚才提到的词向量空间上寻找一下frog这个单词离谁比较相近,这样就可能找到一些词是和frog语义相近的。在自然语言处理中,同义词的表示是非常重要的,因为很多同义词表达的都是一种含义,我们希望在说同义词的时候,机器都能够帮我们准确地理解。
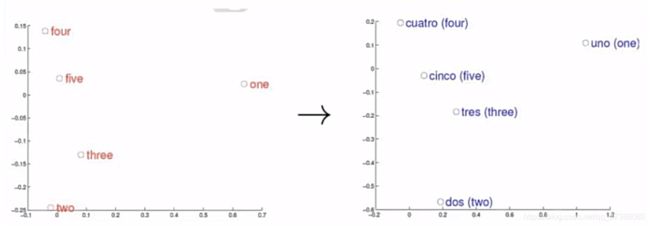
假设指定了两个分布空间,左边是英语,右边是西班牙语,对于这两种语言来说,是否都可以使用词向量来进行建模。建模之后,不同的语言都会有一个分布的空间。比如左边,用英文显示了几个数字的表示(one,two,three,four,five),对西班牙语中的1,2,3,4,5这五个数字构造一个向量空间,构造出来的向量空间如右图所示。虽然使用的是两种不同的语言,但是这五个单词在两个向量空间总的相对位置都是差不多的。这就说明两种语言对应向量空间的结构之间是具有相似性的,从而进一步说明了在词向量,利用刻画词与词之间的相似性是具有一定合理性的。也可以理解词向量的表示核心是利用上下文信息进行词的表示,它与语言的表现形式是无关的,英语和西班牙语单词的不同也并不能影响他们在向量空间上的表示,这就说明词向量的构造实际上更关注的是语言的内在逻辑。所以可以对词向量的分布式表示做一个总结,分布式表示的词向量常见的是数值在-1到1之间,常见的维度为50或者100之间,能够很好地解决语义鸿沟的问题,可以通过向量之间的距离(欧式距离、余弦距离等)来体现词与词的相似性。
如何训练词向量
简单来说,并没有直接的模型可以训练得到分布式表示的词向量,但是可以通过在训练语言模型的同时得到词向量。为了选择某个模型刻画目标词汇与上下文的关系,需要在词向量中抓取到一个词的上下文信息,所以构建上下文与目标词汇的关系最自然的方式也就是使用到语言模型。这里引入论文中提到的连续词袋模型和跳字模型,具体的方法会在后面进行讲解。
(3)前期知识储备
- 语言模型:了解基本的语言模型知识,掌握语言模型的计算方法;
- 词向量:了解词向量的概念和种类,掌握词向量不同表示的优缺点;
- 概率论:了解基本的概率论知识,掌握条件概率的概念和公式;
- 循环神经网络:了解循环神经网络的结构,掌握它的基本工作原理;
第二课时:论文精读(上)
1.论文整体框架
1.1 相关论文:
- 《Distributed Representations of Sentences and Documents》:训练word2vec模型的两个技巧;
- 《word2vec Parameter Learning Explained》:解释word2vec模型参数
- 《word2vec Explained: Deriving Mikolov et al.'s Negative-Sampling Word-Embedding Method》:详细推导负采样过程
1.2 论文结构
2.神经网络语言模型
前面已经了解了语言模型和n-gram模型的概念,当语言模型上升到五元的时候回出现稀疏化的问题,不好统计,平滑的效果也不好,需要把所有的语料过一遍,需要一个很大的存储空间来存储所有词的出现概率,这对于我们要做的任务来说太浪费时间。
解决办法是利用模型参数化的方式构造语言模型,这样就可以不用记录所有的概率,而是只用一组参数去实现这个事情;当计算这个事情时,只需要把所有的词输进去,经过一遍神经网络就可以得到对应的概率。于是神经网络语言模型(NNLM)便提了出来,这是word2vec的前身,该模型直接从语言模型出发,将模型最优化的问题转换为词向量求解的过程。
2.1 介绍改进前的NNLM网络模型
神经网络语言模型(NNLM):直接从语言模型出发,将模型最优化过程转化为求解词向量表示的过程。
- 目标函数(最大似然估计): L ( θ ) = ∑ t l o g P ( w t ∣ w t − n + 1 , . . . , w t − 1 ) L(\theta)=\sum_{t}log P(w_t|w_{t-n+1},...,w_{t-1}) L(θ)=∑tlogP(wt∣wt−n+1,...,wt−1),t是滑动窗口;例如t=4,每次取窗口中的前3个词取去推断下一个词的概率。严格意义来说,这个公式应该是一个乘法公式。但是因为工程原因,得到的概率数会很小,所以把它转化成一个求和log的形式;
- 根据前n-1个词,预测第t个位置单词的概率;
- 使用了非对称的前向窗函数,窗长度为n-1,n就是n-gram中的n;
- 滑动窗口遍历整个语料库求和,计算量正比于语料库大小;
- 概率P满足归一化条件,这样不同位置t处的概率才能相加,即 ∑ w ∈ { v o c a b u l a r y } P ( w ∣ w t − n + 1 , . . . , w t − 1 ) = 1 \sum_{w\in\{vocabulary\}}P(w|w_{t-n+1},...,w_{t-1})=1 ∑w∈{vocabulary}P(w∣wt−n+1,...,wt−1)=1。我们希望模型能够搜索语料库中所有可能的表达,固定一个窗口的大小,假定窗口大小为n=4,窗口不断往前滑,每滑到一个窗口,当前窗口下有4个单词,这里需要满足一个条件,对于四个位置中的前3个位置是已经填好的。举个例子“我爱北京天安门”,这个句子可以看做四个词,已经知道“我”,“爱”,“北京”,预测第四个词“天安门”;在第四个位置,不知道确切的词语是什么的情况下,能添加进去的词是词表中所有的词,也就是说第四个位置的候选基因是整个词表中的词,所以词表中的词每一个添加进去的概率加起来的和为1,即满足归一化的条件。
我们需要模型做的事情是,有一个语料库,通过滑动窗口的形式取出若干个词去预测接下来的词;举个例子,取4-gram,取前面出现的3个词去预测第4个词。
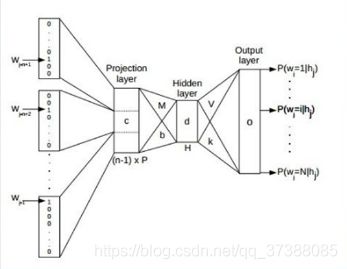
看一下模型结构图:
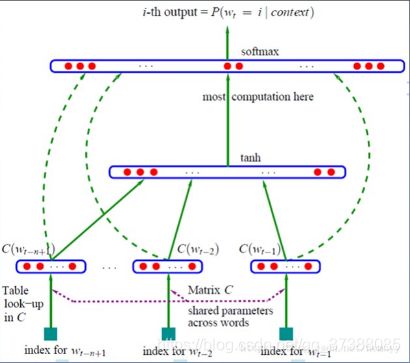
上图中最底下是已经知道的三个词,word-one(w1),word-two(w2),word-three(w3),目标是由w1,w2,w3这三个词去预测w4,这是需要模型最终完成的事情。但是这个过程模型需要重复很多次,模型需要一个一个地去搜索语料库中的词,一个一个地看样本,一个一个地滑动窗口。每一个窗口需要做的事情就是在当前三个词的情况下去预测第四个词。
整体分析模型,模型的输入是一个one-hot表示,如果词表大小是十万,词会被编码为一个十万的词向量,维度为1*100000,上面提到的w1,w2,w3就是这样的向量,词当前的位置为1,其它位置为0。
从one-hot表示到下一层,是一个投影层。分布式词向量的目的就是把所有的词表示成稠密向量,在深度学习中,常用的方法就是先初始化一组权重矩阵,然后不断对这个权重矩阵进行优化。投影层的功能就是这个,在输入层和中间层之间有一个矩阵C,C是十万个词向量中的列向量组合起来的矩阵。比如说有十万个词,希望编码成的稠密向量是300维的,就会得到十万个300维的列向量,组成一个矩阵,这个矩阵就是C。矩阵C是随机初始化的,之后通过神经网络的迭代学习获得我们想要的矩阵。所以矩阵C的维度为300*100000。
w1,w2,w3的维度均为1*1000000的one-hot向量,有一个稠密矩阵C,维度为300*100000,两者相乘,得到的向量的维度为1*300,这相当于从矩阵C中取出一列,因为one-hot向量中只有一个位置为1,其余位置全为0。具体乘法步骤如下图所示。

为什么叫投影层,因为我们用一个one-hot表示把矩阵C中对应的w1这个词取出来,这就相当于一个投影。不用纠结于矩阵C为什么取300维,这只是为了举例说明。在工程中一般认为,在大语料情况下,300到500维之间才有意义,不然表示不出词与词之间的细微差别。
仔细观察整个过程,可以发现和数学非常相关。投影层之后,w1、w2和w3都有了对应的稠密向量。接着把这三个稠密向量拼接起来,300维的3个稠密向量就变为了900维的一个稠密向量。
拼接完成后,就是我们熟悉的神经网络部分,模型衔接一个隐藏层,隐藏层也有一个维度,假设为500维。接着将900维的稠密向量作为输入和隐藏层中的500维做一个全连接,最后用非线性激活函数激活。
模型最后一层是一个softmax线性分类器,目的是判断“我爱北京”这三个词之后到底接的是哪一个词。模型没办法直接对输出进行预测,所以我们经常做的事情是把词表中的10万个词铺开,模型会输出第四个词属于十万个词中每个词的概率是多少。所以模型最后输出的是一个1*100000的概率向量,我们希望“天安门”这个词在概率向量中的概率值是最大的。以上就是整个神经网络语言模型的结构。
神经网络语言模型的输入是固定的,是十万维的One-hot向量。在训练过程中,最后的输出也是已知的。最后的output可以看做一个十万维的向量,这个向量只有一个位置是1,其它位置全部为0。在输入和输出都已知的条件下,模型会根据输出做一个优化,使用交叉熵作为损失函数,通过最小化损失函数优化参数。优化后之后的矩阵C就是我们想要的词向量,也就是说这个投影层的权重是我们最后想得到的词向量。
总结一下神经网络语言模型的各层结构,神经网络语言模型各层结构如下图所示:
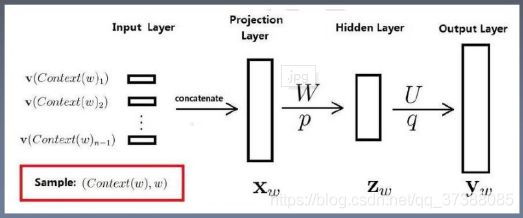
- 输入层(input):输入(N-1)个前向词,One-hot表示。
- 投影层(projection layer):采用线性投影方式将词向量投影到稠密D维表示,并拼接起来,方便输入到隐藏层中。
- 隐藏层(hidden layer):做全连接,全连接“神经元”用户自定。
- 输出层(output):隐藏层到输出层是全连接,softmax分类器。
整个过程通过不断输入批次数据,对网络以梯度下降的方式进行反向传播,在反向传播的过程中对参数进行不断更新,最后训练出一个进行词预测的任务模型,并且将训练好的模型中的C矩阵中每一列都作为对应one-hot编码中位置为1的词向量大小,这里的大小指的是1*300的维度。这个词向量就是我们最后要转化的结果。
Q = N ∗ D + N ∗ D ∗ H + H ∗ V Q=N*D + N*D*H + H*V Q=N∗D+N∗D∗H+H∗V
- 投影层的计算复杂度为 N ∗ D N*D N∗D,N为输入词语的个数,D是词向量的维度,也就是上面设定的300维;
- 隐藏层的计算复杂度为 N ∗ D ∗ H N*D*H N∗D∗H,H是隐藏层的节点数,上面假定为500维,因为投影层是将输入进行拼接,所以全连接层的输入为N*D,输出为H,所以整体的计算复杂度为 N ∗ D ∗ H N*D*H N∗D∗H;
- 输出层的计算复杂度为 H ∗ V H*V H∗V,V是输出向量的维数,也就是词表的大小。
一个简单模型在大数据量上的表现比复杂模型在少数据量上的表现会好。
接着看另一种本质相同的神经网络语言模型。
2.2 循环神经网络语言模型(RNNLM)
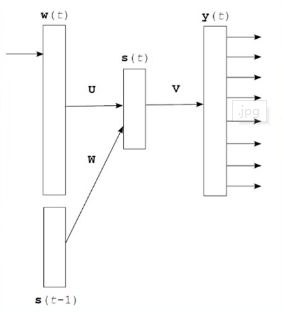
循环神经网络语言模型(RNNLM):基于循环神经网络的语言模型。
上图就是简单的循环神经网络语言模型的结构,其中t代表时间;
- w ( t ) w(t) w(t)表示第 t t t个时刻的当前输入单词,需要转换为词向量;
- s ( t − 1 ) s(t-1) s(t−1)表示隐藏层的前一次输出;
- s ( t ) s(t) s(t)表示当前时刻隐藏层的输出;
- y ( t ) y(t) y(t)表示在当前时刻 w ( t ) w(t) w(t)和前一时刻隐藏层 s ( t − 1 ) s(t-1) s(t−1)的输入下,句子接当前词的概率;
输入层:和NNLM一样,需要将当前时间步的one-hot表示的单词转化为词向量;
隐藏层:对输入和上一个时间步的隐藏输出进行全连接层操作;
s ( t ) = U ∗ w ( t ) + W ∗ s ( t − 1 ) + d s(t)=U*w(t)+W*s(t-1)+d s(t)=U∗w(t)+W∗s(t−1)+d
输出层:一个全连接层,后面接一个softmax函数来生成概率分布;
y ( t ) = b + V ∗ s ( t ) y(t)=b+V*s(t) y(t)=b+V∗s(t)
其中y是一个 1 ∗ V 1*V 1∗V的向量:
P ( w t ∣ w t − n + 1 , … , w t − 1 ) = exp ( y w t ) ∑ i exp ( y i ) P\left(w_{t} \mid w_{t-n+1}, \ldots, w_{t-1}\right)=\frac{\exp \left(y_{w_{t}}\right)}{\sum_{i} \exp \left(y_{i}\right)} P(wt∣wt−n+1,…,wt−1)=∑iexp(yi)exp(ywt)
循环神经网络语言模型,每个时间步预测一个词,在预测第n个词时使用了前n-1个词的信息。

循环神经网络的损失函数为:
Loss: L = − 1 T ∑ i = 1 T log p ( w i ∣ w 1 , … , w i − 1 ) \text { Loss: } L=-\frac{1}{T} \sum_{i=1}^{T} \log p\left(w_{i} \mid w_{1}, \dots, w_{i-1}\right) Loss: L=−T1i=1∑Tlogp(wi∣w1,…,wi−1)
之所以称为循环神经网络语言模型,就是 t t t时刻, s ( t ) s(t) s(t)会留下一个副本,在 t + 1 t+1 t+1时刻, s ( t ) s(t) s(t)会送到输出层,这样就相当于一个循环。循环神经网络语言模型最大优势在于可以真正地充分利用所有上下文信息来预测下一个词。而不是像前一个模型那样,只能开一个n个词的窗口,用前n-1个词来预测下一个词。从形式上看,这是一个非常终极的模型,毕竟语言模型能用到的信息该模型全都能用上,但是非常可惜的是循环神经网络语言模型在形式上非常好看,但是使用起来却是非常难以优化的。如果优化得不好,长距离的信息就会丢失,甚至还无法达到之前的模型那样开窗口看之前若干个词的效果。
计算复杂度: Q = H ∗ H + H ∗ V Q=H*H + H*V Q=H∗H+H∗V
- H是隐藏层的节点数
传统神经网络语言模型的缺点
- 计算复杂度过大:
- NNLM: Q = N ∗ D + N ∗ D ∗ H + H ∗ V Q=N*D + N*D*H + H*V Q=N∗D+N∗D∗H+H∗V,复杂度最大为隐藏层到输出层,即 H ∗ V H*V H∗V部分,因为输出是以词表大小作为维度的向量,这个维度通常在万级以上,因为语料库中的词通常在万级以上的。论文中提出一种分层softmax方法,能让计算复杂度减小到 l o g V logV logV,这样模型的复杂度主要由 N ∗ D ∗ H N*D*H N∗D∗H决定,也就是投影层到隐藏层的部分。
- RNNLM: Q = H ∗ H + H ∗ V Q=H*H + H*V Q=H∗H+H∗V,复杂度主要在 H ∗ V H*V H∗V,同样能经过分层softmax方法降低到 l o g V log V logV,复杂度开销最大变为 H ∗ H H*H H∗H。
- 参数更多
有没有什么办法可以解决计算复杂度比较大、参数较多的问题呢?word2vec的提出为解决这些问题应运而生了。word2vec的两个模型CBOW和Skip-gram能够很好地改善这种情况,不用大规模的计算就可以得到需要的词向量。具体的模型在下一节进行介绍。
3.语言模型评价指标——困惑度(Perplexity)
P ( s ) = P ( w 1 , w 2 , … , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) … P ( w n ∣ w 1 w 2 … w n − 1 ) P(s)=P\left(w_{1}, w_{2}, \dots, w_{n}\right)=P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) \dots P\left(w_{n} \mid w_{1} w_{2} \dots w_{n-1}\right) P(s)=P(w1,w2,…,wn)=P(w1)P(w2∣w1)…P(wn∣w1w2…wn−1)
P P ( s ) = P ( w 1 , w 2 , … , w n ) − 1 n = 1 P ( w 1 , w 2 , … , w n ) n P P(s)=P\left(w_{1}, w_{2}, \dots, w_{n}\right)^{-\frac{1}{n}}=\sqrt[n]{\frac{1}{P\left(w_{1}, w_{2}, \dots, w_{n}\right)}} PP(s)=P(w1,w2,…,wn)−n1=nP(w1,w2,…,wn)1
句子概率越大,语言模型越好,困惑度越小;
3.1 语言模型困惑度与Loss关系
对一句话求其损失,T是句子中词的个数:
Loss: L = − 1 T ∑ i = 1 T log p ( w i ∣ w i − n + 1 , … , w i − 1 ) \text { Loss: } L=-\frac{1}{T} \sum_{i=1}^{T} \log p\left(w_{i} \mid w_{i-n+1}, \dots, w_{i-1}\right) Loss: L=−T1i=1∑Tlogp(wi∣wi−n+1,…,wi−1)
P P ( s ) = P ( w 1 , w 2 , … , w T ) − 1 T = 1 P ( w 1 , w 2 , … , w T ) T P P(s)=P\left(w_{1}, w_{2}, \dots, w_{T}\right)^{-\frac{1}{T}}=\sqrt[T]{\frac{1}{P\left(w_{1}, w_{2}, \dots, w_{T}\right)}} PP(s)=P(w1,w2,…,wT)−T1=TP(w1,w2,…,wT)1
对困惑度公式取对数:
log ( P P ( s ) ) = − 1 T log ( P ( w 1 ) P ( w 2 ∣ w 1 ) … P ( w T ∣ w T − n + 1 , … , w T − 1 ) ) \log (P P(s))=-\frac{1}{T} \log \left(P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) \ldots P\left(w_{T} \mid w_{T-n+1}, \dots, w_{T-1}\right)\right) log(PP(s))=−T1log(P(w1)P(w2∣w1)…P(wT∣wT−n+1,…,wT−1))
log ( P P ( s ) ) = − 1 T ( log P ( w 1 ) + log P ( w 2 ∣ w 1 ) + ⋯ + log P ( w T ∣ w T − n + 1 , … , w T − 1 ) \log (P P(s))=-\frac{1}{T}\left(\log P\left(w_{1}\right)+\log P\left(w_{2} \mid w_{1}\right)+\cdots+\log P\left(w_{T} \mid w_{T-n+1}, \dots, w_{T-1}\right)\right. log(PP(s))=−T1(logP(w1)+logP(w2∣w1)+⋯+logP(wT∣wT−n+1,…,wT−1)
log ( P P ( s ) ) = − 1 T ∑ i = 1 T log p ( w i ∣ w i − n + 1 , … , w i − 1 ) \log (P P(s))=-\frac{1}{T} \sum_{i=1}^{T} \log p\left(w_{i} \mid w_{i-n+1}, \dots, w_{i-1}\right) log(PP(s))=−T1i=1∑Tlogp(wi∣wi−n+1,…,wi−1)
P P ( s ) = e L P P(s)=e^{L} PP(s)=eL
4.课时小结
- 摘要:论文高度概括,包含作者研究思路;
- 介绍:简述论文背景,提出写作目的,介绍前人工作;
- 模型结构:神经网络语言模型和循环神经网络语言模型;
第三课时:论文精读(下)
Word2vec 原理
- 语言模型基本思想:句子中下一个词的出现和前面的词是有关系的,所以可以使用前面的词预测下一个词;
- Word2vec基本思想:句子中相近的词之间是有联系的,比如今天后面经常出现上午、下午和晚上。所以Word2vec的基本思想就是用词来预测词。skip-gram使用中心词预测周围词,cbow使用周围词预测中心词;
前面学习了神经网络语言模型,严格意义上来说,它的效果还是不错的,但是计算量非常大,我们希望可以使用尽量少的计算资源得到我们想要的结果。所以作者提出了word2vec模型,word2vec就是简化版的神经网络语言模型,它实际上也是训练了一个语言模型,通过语言模型来获取词向量。
语言模型就是通过前n个词预测下一个词的概率,简单来说就是一个多分类器,简单总结神经网络语言模型的过程,输入词到one-hot表示,再连接一个全连接层,再连接若干层,最后接一个softmax分类器,就得到语言模型。
我们要做的就是将大批的文本输入训练,最后得到的第一个全连接层的参数就是词向量表。Word2vec中包含两种模型的算法,分别为CBOW和Skip-gram模型。
1.CBOW模型——介绍word2vec工具中的连续词袋模型
-
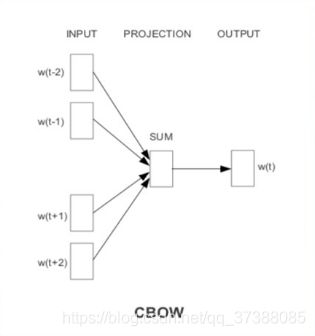
CBOW:Continuous Bag of Words,连续词袋模型,即利用中心词(Wt)的上下文(Context)来预测中心词(Wt)。
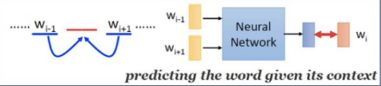
在上图中的CBOW模型中,输入的是已知的上下文词语,输出的是中心词 w i w_i wi。 -
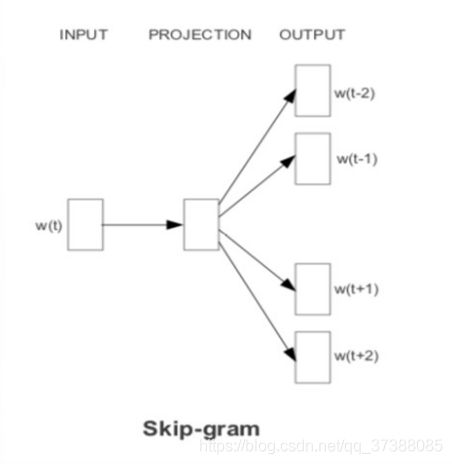
Skip-gram:跳字模型,是根据中心词(Wt)来预测周围的词,即预测上下文(Context)。
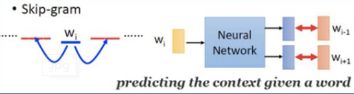
在上图的Skip-gram模型中,是根据中心词w_t来预测周围的词,也就是根据中心词来预测上下文。
CBOW模型和Skip-gram模型实际上是word2vec模型的两种不同思想的实现。
1.1 CBOW算法
- 目标函数: ι = ∑ w ∈ C l o g p ( w ∣ C o n t e x t ( w ) ) \iota = \sum_{w\in C}log p(w|Context(w)) ι=∑w∈Clogp(w∣Context(w))
- 连续词袋模型是通过上下文来预测中心词,所以很容易得到目标函数;就是已知上下文的词去预测中心词的概率,然后求一个最大似然估计函数。
- 使用双向上下文窗口
- 如下图,连续词袋模型的结构图相与神经网络语言模型相比,少了一些东西。通过结构图可以发现CBOW没有隐藏层,经过投影层之后不仅仅做向量的拼接,而是做了一个求和。为什么使用求和运算呢?之前我们在计算神经网络语言模型复杂度的时候,尽管使用分层softmax模型使隐藏层到输出层的计算复杂度由 H ∗ V H*V H∗V变成了 l o g V log V logV,但是由投影层到隐藏层的计算复杂度仍然很大。所以连续词袋模型(CBOW)干脆去掉了隐藏层,并且神经网络语言模型在得到每一个初始化的词向量之后,在投影层做的是拼接运算。比如上面举的例子,如果初始化的词向量是300维,输入四个词之后,拼接得到的词向量就是1200维的,词向量的维度就变得非常高了。所以在连续词袋模型中,就不进行拼接操作了。把拼接换成了向量的求和操作,求和之后还会做一个平均,用平均之后的词向量去预测中心词。这样我们不难理解为什么word2vec可以在CPU上运行,而且速度也相对较快,这就是因为减少了很多不必要的计算,模型已经省略了很多运算。
- 无隐层
- 对比于神经网络语言模型, CBOW模型使用双向上下文窗口,并且与上下文词序无关。也就是说,上下文所有的词对当前词出现的概率的影响权重是一样的。这也解释了模型为什么叫连续词袋模型,就如同在袋子中取词,取出数量足够的词就可以了。和取出词的前后顺序是没有关系的。
- 上下文词序无关(BoW)
- 输入层直接使用低维稠密向量表示
- 投影层简化为求和(平均)
用一个实例简单介绍一下CBOW模型的计算过程,假设语料库中只有四个简单的单词“I drink coffee everyday”,做这样的假设是为了在做参数表示的时候更加直观,实际语料库中词语一般都在万级以上,而且word2vec必须在大语料上训练才可以看到效果。
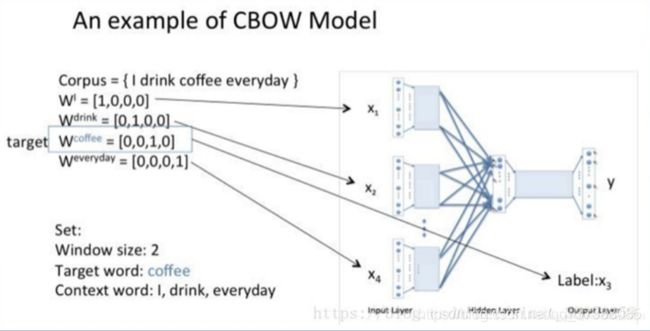
如上图所示,选择coffee作为中心词,窗口大小设为2,也就是说需要根据单词“I”,“drink”,“everyday”来预测“coffee”这个单词。
首先输入“I”,“drink”,“everyday”这三个单词的one-hot表示作为输入的上下文单词,而“coffee”作为经过连续词袋模型后要求的目标词语。
接着给一个初始化权重W,这个初始化权重矩阵的维度就是 V ∗ N V*N V∗N,也就是说,行数是我们设定的词向量的维度,为了直观,取值为3。实际上取值应该为300到500维的中间数,N是词表的大小,对于整个词表来说,N的值为4。
让权重矩阵乘于输入单词的one-hot表示,所得到的向量就是每个词的词向量。注意一下,这里的权重矩阵W和上面讲到的矩阵C一样,这就是模型最后需要求解得到的副产品——词向量的嵌入矩阵,这也是我们使用模型的真正目的。
W矩阵一开始是是随机初始化的,可以使用高斯分布等进行初始化,在训练过程中,会根据损失函数不断迭代调整矩阵的参数,学习完的优化矩阵就是真正的词向量矩阵。
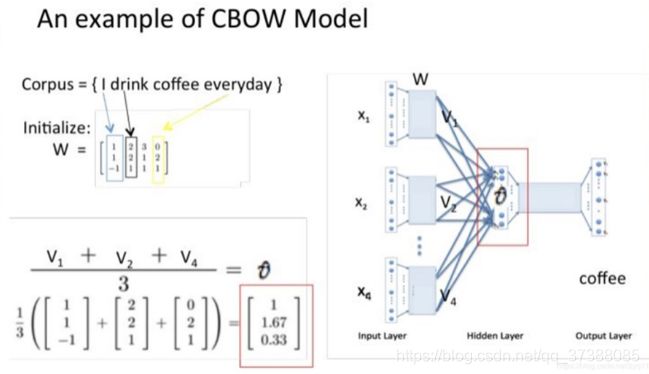
和神经网络语言模型相似,矩阵W和单词的one-hot向量相乘就相当于取出了各个词的词向量,如上图,可以看到“I”这个词做运算后,取出的向量是 [ 1 , 1 , − 1 ] [1,1,-1] [1,1,−1],“drink”取出的向量是 [ 2 , 2 , 1 ] [2,2,1] [2,2,1],“everyday”对应的词向量是 [ 0 , 2 , 1 ] [0,2,1] [0,2,1]。
进行乘法运算后词向量到达隐藏层,将得到的词向量进行求和取平均运算,最后得到了 v v v向量。这里的隐藏层和神经网络语言模型的隐藏层是不一样的,这里的隐藏层是投影层,只是改了一下叫法。
隐藏层到输出层之间有一个权重矩阵 W ′ W^{'} W′,这个输出权重矩阵是随机初始化得到的,维度为 N ∗ V N*V N∗V,N是语料库的大小,“V”是词向量的维数,设置这个维数的含义是什么呢?
输出权重矩阵乘于上一层得到的求和平均向量V后得到的是一个4*1维的向量,也就是说得到的这四个数经过最后的softmax线性计算就可以作为语料库词的概率表示。
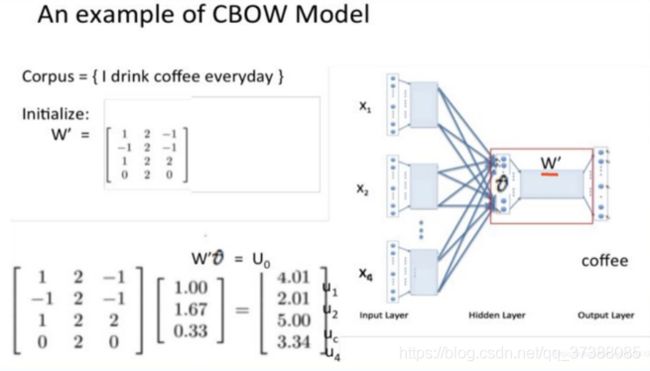
从图中可以看到得到的向量为 [ 4.01 , 2.01 , 5.00 , 3 , 34 ] [4.01,2.01,5.00,3,34] [4.01,2.01,5.00,3,34],其中的4.01表示的就是第一个单词,2.01表示第二个单词,5.00就是实际想要得到的单词“coffee”,3.44也就是第四个单词。
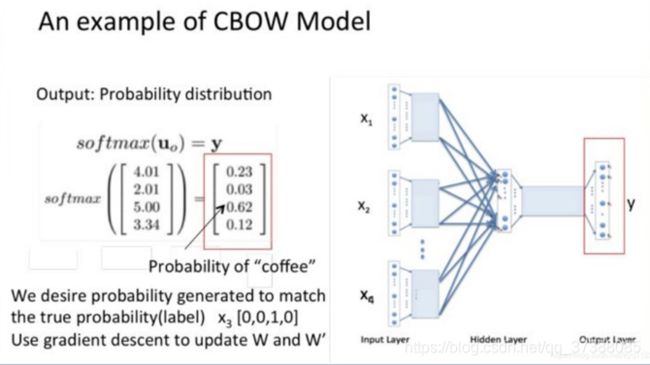
最后把上面得到的向量经过softmax层激活函数处理,得到了具有词表格维度的概率分布,其中概率最大的索引指示的就是刚才预测出的中间词。从上图中可以看到第三个词“coffee”正是我们想要的单词。
在训练过程中,把概率,也就是现在的0.62与“coffee”这个词的one-hot做比较,用随机梯度下降法更新权重矩阵 W W W和 W ′ W^{'} W′,我们希望计算的误差越小越好。这里假设我们此时得到的概率分布已经达到了设定的迭代次数。现在训练出来的矩阵 W W W就可以当做是word2vec的词向量表。
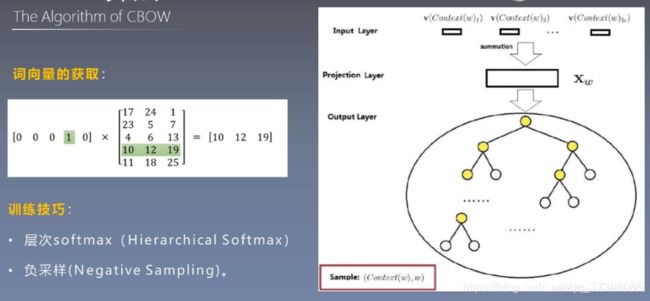
求对应单词的词向量就是一个查表的过程,任何一个单词的one-hot表示乘于矩阵 W W W都可以得到自己的词向量。上图的右侧图是整个连续词袋模型的网络结构,可以看到输入的是初始化向量,然后通过中心词周围的词进行向量求和,最后进行softmax激活函数就找到了概率最大的词向量。
在刚才的例子中,词表中只有四个词,运算相对简单,但实际上如果词表是十万级或者百万级以上,计算量仍然很大。所以google工程师就对word2vec的训练过程做了优化。优化的方式有两种,层次softmax(Hierarchical softmax)和负采样(Negative sampling)。
上图右侧圆圈中的层次softmax就是运用了哈夫曼树的相关知识,关于这两种技巧的具体原理先不做过多的解释。可以根据前面关于word2vec推荐的论文自行查阅学习。
训练连续词袋模型
连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。在同样的文本序列“the”,“man”,“loves”,“his”,“son”里,以“loves”为中心词。且背景窗口大小为2时,连续词袋模型关心的是,给定背景词“the”,“man”,“his”,“son”生成中心词“loves”的条件概率(如下图所示),也就是:
P ( " l o v e s " ∣ " t h e " , " m a n " , " h i s " , " s o n " ) P( "loves" | "the ", "man", "his", "son") P("loves"∣"the","man","his","son")
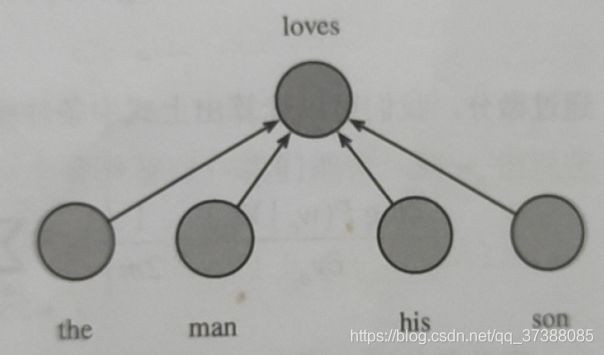
因为连续词袋模型的背景词有多个,我们将这些背景词向量取平均。设 v i ∈ R d \boldsymbol{v}_{i} \in \mathbb{R}^{d} vi∈Rd和 u i ∈ R d \boldsymbol{u}_{i} \in \mathbb{R}^{d} ui∈Rd分别表示词典中索引为i的词作为背景词和中心词的向量。设中心词 w c w_c wc在词典中索引为c,背景词 w o 1 , . . . , w o 2 m w_{o_1},...,w_{o_{2m}} wo1,...,wo2m在词典中的索引为 o 1 , . . . , o 2 m o_1,...,o_{2m} o1,...,o2m,那么给定背景词生成中心词的条件概率为:
P ( w c ∣ w 0 1 , ⋯ , w o 2 m ) = exp ( 1 2 m u c ⊤ ( v 0 1 + ⋯ + v 2 ln ) ) ∑ i ∈ V exp ( 1 2 m u i ⊤ ( v 0 1 + ⋯ + v 0 2 m ) ) P\left(w_{c} \mid w_{0_{1}}, \cdots, w_{o_{2 m}}\right)=\frac{\exp \left(\frac{1}{2 m} \boldsymbol{u}_{c}^{\top}\left(\boldsymbol{v}_{0_{1}}+\cdots+\boldsymbol{v}_{2_{\ln }}\right)\right)}{\sum_{i \in V} \exp \left(\frac{1}{2 m} \boldsymbol{u}_{i}^{\top}\left(\boldsymbol{v}_{0_{1}}+\cdots+\boldsymbol{v}_{0_{2 m}}\right)\right)} P(wc∣w01,⋯,wo2m)=∑i∈Vexp(2m1ui⊤(v01+⋯+v02m))exp(2m1uc⊤(v01+⋯+v2ln))
为了使符号更加简单,我们记 W o = { w o 1 , ⋯ , w o 2 m } \mathcal{W}_{o}=\left\{w_{o_{1}}, \cdots, w_{o_{2 m} }\right\} Wo={wo1,⋯,wo2m},且 v ˉ o = ( v o 1 + ⋯ + v o 2 m ) / ( 2 m ) \bar{v}_{o}=\left(v_{o_{1}}+\cdots+v_{o_{2 m}}\right) /(2 m) vˉo=(vo1+⋯+vo2m)/(2m),那么上式可以简写成:
P ( w c ∣ W o ) = exp ( u c ⊤ v ‾ o ) ∑ i ∈ V exp ( u i ⊤ v ‾ o ) P\left(w_{c} \mid \mathcal{W}_{o}\right)=\frac{\exp \left(\boldsymbol{u}_{c}^{\top} \overline{\boldsymbol{v}}_{o}\right)}{\sum_{i \in V} \exp \left(\boldsymbol{u}_{i}^{\top} \overline{\boldsymbol{v}}_{o}\right)} P(wc∣Wo)=∑i∈Vexp(ui⊤vo)exp(uc⊤vo)
给定一个长度为T的文本序列,设时间步t的词为 w ( t ) w^{(t)} w(t),背景窗口大小为m,连续词袋模型的似然函数是由背景词生成任一中心词的概率:
∏ t = 1 T P ( w ( t ) ∣ w ( t − m ) , ⋯ , w ( t − 1 ) , w ( t + 1 ) , ⋯ , w ( t + m ) ) \prod_{t=1}^{T} P\left(w^{(t)} \mid w^{(t-m)}, \cdots, w^{(t-1)}, w^{(t+1)}, \cdots, w^{(t+m)}\right) t=1∏TP(w(t)∣w(t−m),⋯,w(t−1),w(t+1),⋯,w(t+m))
训练连续词袋模型时,连续词袋模型的最大似然估计等价于最小化损失函数:
− ∑ t = 1 T log P ( w ( t ) ∣ w ( t − m ) , ⋯ , w ( t − 1 ) , w ( t + 1 ) , ⋯ , w ( t + m ) ) -\sum_{t=1}^{T} \log P\left(w^{(t)} \mid w^{(t-m)}, \cdots, w^{(t-1)}, w^{(t+1)}, \cdots, w^{(t+m)}\right) −t=1∑TlogP(w(t)∣w(t−m),⋯,w(t−1),w(t+1),⋯,w(t+m))
注意到
log P ( w c ∣ W o ) = u c ⊤ v ‾ o − log ( ∑ i ∈ V exp ( u i ⊤ v ‾ o ) ) \log P\left(w_{c} \mid \mathcal{W}_{o}\right)=\boldsymbol{u}_{c}^{\top} \overline{\boldsymbol{v}}_{o}-\log \left(\sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \overline{\boldsymbol{v}}_{o}\right)\right) logP(wc∣Wo)=uc⊤vo−log(i∈V∑exp(ui⊤vo))
通过微分,我们可以计算出上式中条件概率的对数有关任一背景词向量 v o i ( i = 1 , ⋯ , 2 m ) v_{o_{i}}(i=1, \cdots, 2 m) voi(i=1,⋯,2m)的梯度为:
∂ log P ( w c ∣ W o ) ∂ v o i = 1 2 m ( u c − ∑ j e V exp ( u j ⊤ v ˉ o ) u j ∑ i ∈ V exp ( u i ⊤ v ˉ o ) ) = 1 2 m ( u c − ∑ j ∈ V P ( w j ∣ W o ) u j ) \frac{\partial \log P\left(w_{c} \mid \mathcal{W}_{o}\right)}{\partial v_{o_{i}}}=\frac{1}{2 m}\left(u_{c}-\sum_{j_{e} V} \frac{\exp \left(u_{j}^{\top} \bar{v}_{o}\right) u_{j}}{\sum_{i \in V} \exp \left(u_{i}^{\top} \bar{v}_{o}\right)}\right)=\frac{1}{2 m}\left(u_{c}-\sum_{j \in \mathcal{V}} P\left(w_{j} \mid \mathcal{W}_{o}\right) u_{j}\right) ∂voi∂logP(wc∣Wo)=2m1⎝⎛uc−jeV∑∑i∈Vexp(ui⊤vˉo)exp(uj⊤vˉo)uj⎠⎞=2m1⎝⎛uc−j∈V∑P(wj∣Wo)uj⎠⎞
有关其它词向量的梯度同理可得,同跳字模型不同的一点在于,我们一般使用连续词袋模型的背景词向量作为词的表征向量。
1.2 Skip-gram算法 —— 跳字模型
- 利用中心词来预测上下文词
- 目标函数: £ = ∑ w ∈ C l o g p ( C o n t e x t ( w ) ∣ w ) \pounds =\sum_{w\in C}log \space p(Context(w)|w) £=∑w∈Clog p(Context(w)∣w)
- 输入层:只含当前样本的中心词w的词向量;
- 投影层:恒等投影,为了和CBOW模型对比;恒等投影,输入和输出是一样的;
- 输出层:和CBOW模型一样,输出层也是一颗Huffman树;
在看具体的运算流程之前,先给大家强调一下滑动窗口的两个参数,其中一个参数为skip_window,代表着从当前输入词的一侧,左边或者右边选取出词的数量。下图中有一个句子,设置skip_window的参数为2,假设当前输入的中心词是the,那么最终获得窗口中的词就是the quick brown,因为the左边没有词。当中心词左右两边都有两个词时,那就都可以把左右两边的词放进窗口,因为skip_window设置为2。随着滑动窗口一直在移动,整个窗口中锁定的词也在不断地变化;另一个常数叫num_skips,代表的是从整个窗口中选取多少个不同的词作为输出的上下文。设skip_window的参数为2,num_skips的参数设定为2。以the为中心词时,可以得到两组训练数据(the,quick)和(the,brown)。当以quick为中心单词的时候,就会得到三组输入输出形式的训练数据(quick,the),(quick,brown),(quick,fox)。以此类推,所得到的单词段就是需要得到的输出。
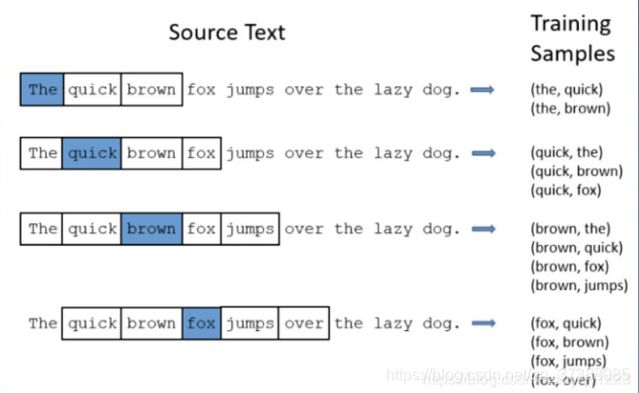
接下来看一下跳字模型的训练过程。
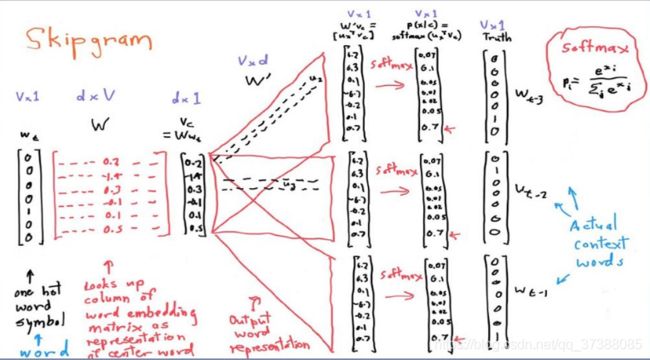
首先给定一个输入的中心词,以one-hot形式表示,维度为 V ∗ 1 V*1 V∗1, V V V是词表的大小。可以看到图中给出的是一个七维的向量;接着是一个随机初始化权重矩阵 w w w,矩阵维度为 d ∗ V d*V d∗V, d d d是我们想要得到的词向量的维度。用输入词的one-hot表示乘于这个权重矩阵 w w w得到的是一个 d ∗ 1 d*1 d∗1维的词向量 V c V_c Vc,这个词向量可以理解成输入词的分布式词向量表示。接着是一个 V ∗ d V*d V∗d维的初始化权重矩阵 W ′ W' W′,也就是用刚才得到的词向量 V c V_c Vc去乘于矩阵 W ′ W' W′,得到的就是输出向量。输出向量经过softmax函数,变成一个概率,然后就可以找到对应位置概率最大的判断为预测单词。根据位置写对应输出的one-hot向量,进而确定是哪个单词。 W ′ W' W′矩阵具有相同的参数,因此每次训练的时候就分别用中心词上下文对所有目标单词去计算最大交叉熵,目的就是最小化所有条件分布的乘积。优化后的 W W W矩阵仍然是我们希望得到的词向量矩阵。
假设给定一个长度为T的文本序列,设时间步t的词为 w ( t ) w^{(t)} w(t),,假设给定中心词情况下背景词的生成相互独立,假设背景窗口大小为m。跳字模型的参数是每个词所对应的中心词向量和背景词向量。训练中我们通过最大化似然函数来学习模型参数,即最大似然估计。这等价于最小化以下损失函数:
− ∑ t = 1 T ∑ − m ⩽ j ⩽ m , j ≠ 0 log P ( w ( t + j ) ∣ w ( t ) ) -\sum_{t=1}^{T} \sum_{-m \leqslant j \leqslant m, j \neq 0} \log P\left(w^{(t+j)} \mid w^{(t)}\right) −t=1∑T−m⩽j⩽m,j=0∑logP(w(t+j)∣w(t))
如果使用随机梯度下降,那么在每一次迭代里我们随机采样一个较短的子序列来计算有关该子序列的损失,然后计算梯度来更新模型参数。梯度计算的关键是条件概率的对数有关中心词向量和背景词向量的梯度。根据定义,首先看到:
log P ( w o ∣ w c ) = u o ⊤ v c − log ( ∑ i ∈ V exp ( u i ⊤ v c ) ) \log P\left(w_{o} \mid w_{c}\right)=\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}-\log \left(\sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \boldsymbol{v}_{c}\right)\right) logP(wo∣wc)=uo⊤vc−log(i∈V∑exp(ui⊤vc))
通过微分,我们可以得到上面公式中的 v c v_c vc的梯度:
∂ log P ( w o ∣ w c ) ∂ v c = u o − ∑ j ∈ V exp ( u j ⊤ v c ) u j ∑ i ∈ V exp ( u i ⊤ v c ) \frac{\partial \log P\left(w_{o} \mid w_{c}\right)}{\partial v_{c}}=u_{o}-\frac{\sum_{j \in V} \exp \left(u_{j}^{\top} v_{c}\right) u_{j}}{\sum_{i \in V} \exp \left(u_{i}^{\top} v_{c}\right)} ∂vc∂logP(wo∣wc)=uo−∑i∈Vexp(ui⊤vc)∑j∈Vexp(uj⊤vc)uj
= u o − ∑ j ∈ V ( exp ( u j ⊤ v c ) ∑ i ∈ V exp ( u i ⊤ v c ) ) u j =u_{o}-\sum_{j \in \mathcal{V}}\left(\frac{\exp \left(u_{j}^{\top} v_{c}\right)}{\sum_{i \in V} \exp \left(u_{i}^{\top} v_{c}\right)}\right) u_{j} =uo−j∈V∑(∑i∈Vexp(ui⊤vc)exp(uj⊤vc))uj
= u o − ∑ j ∈ V P ( w j ∣ w c ) u j =u_{o}-\sum_{j \in V} P\left(w_{j} \mid w_{c}\right) u_{j} =uo−j∈V∑P(wj∣wc)uj
它的计算需要词典中所有词以 w c w_c wc为中心词的条件概率,有关其它词向量的梯度同理可得。
训练结束后,对于词典中的任一索引为i的词,我们均得到该词作为中心词和背景词的两组词向量 v i v_i vi和 u i u_i ui。在自然语言处理中,一般使用跳字模型的中心词向量作为词的表征向量。
2.Word2vec模型复杂度讨论
回忆上面的内容,跳字模型的核心在于使用softmax运算得到给定中心词 w c w_c wc来生成背景词 w o w_o wo的条件概率:
P ( w o ∣ w c ) = exp ( u o ⊤ v c ) ∑ i ∈ V exp ( u i ⊤ v c ) P\left(w_{o} \mid w_{c}\right)=\frac{\exp \left(\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}\right)}{\sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \boldsymbol{v}_{c}\right)} P(wo∣wc)=∑i∈Vexp(ui⊤vc)exp(uo⊤vc)
该条件概率相应的对数损失为:
− log P ( w o ∣ w c ) = − u o ⊤ v c + log ∑ i ∈ V exp ( u i ⊤ v c ) -\log P\left(w_{o} \mid w_{c}\right)=-\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}+\log \sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \boldsymbol{v}_{c}\right) −logP(wo∣wc)=−uo⊤vc+logi∈V∑exp(ui⊤vc)
由于softmax运算考虑了背景词可能是词典V中的任一词,以上损失包含了词典大小数目的项的累加。在上面进行跳字模型或者连续词袋模型的参数推导时,由于条件概率使用了softmax运算,每一步的梯度计算都包含词典大小数目的项的累加。对于含有几十万或者上百万词的较大词典来说,每次的梯度计算开销可能过大。为了降低该计算复杂度,这里将介绍两种近似训练方法,负采样和层次softmax。
2.1 层次softmax
注意到,原始方法使用softmax运算考虑了背景词可能是词典中的任一词,假设词典有40000个词,softmax每次需要运算40000次。为了降低计算开销,我们先假设考虑使用两层的树结构来组织词表,即将词表中的词分成K组,并且每个词只能属于一个分组,每组大小为 v K \frac{v}{K} Kv。当词表大小为40000时,将词表中的所有词分到200组,每组200个词。这样只需要计算两次200类的softmax,比直接计算40000类的softmax加快100倍。
为了进一步降低softmax函数的计算复杂度,我们可以使用更深层的树结构来组织词汇表。假设用二叉树来组织词表中的所有词,二叉树的叶子节点代表词表中的词,非叶子结点表示不同层次上的类别。
如果我们使用平衡二叉树来进行分类,则条件概率估计可以转换为 l o g 2 ∣ V ∣ log_2|V| log2∣V∣个二分类问题,这时原始预测模型中的softmax函数可以使用logistic函数代替,计算效率可以加速 ∣ V ∣ l o g 2 ∣ V ∣ \frac{|V|}{log_2|V|} log2∣V∣∣V∣。
注意到,词典中每个词出现的次数(概率)是不同的,如果我们将词典转化为平衡二叉树,则出现频率高的词的条件概率估计开销和出现概率低的词的条件概率估计开销一样,这样会增加计算开销。如果让出现频率高的词更接近根节点,则能有效降低计算开销。这就相当于构建一个带权重的最短路径二叉树,也就是构建一个哈夫曼树。
层次softmax的构建
如下图,每一个非叶子结点都是一个向量,在跳字模型中,假设中心词词向量为 v c v_c vc,要求词I的概率,则可以表示为:
p ( I ∣ c ) = σ ( θ 0 T v c ) σ ( θ 1 T v c ) ( 1 − σ ( θ 2 T v c ) ) p(\mathrm{I} \mid c)=\sigma\left(\theta_{0}^{T} v_{c}\right) \sigma\left(\theta_{1}^{T} v_{c}\right)\left(1-\sigma\left(\theta_{2}^{T} v_{c}\right)\right) p(I∣c)=σ(θ0Tvc)σ(θ1Tvc)(1−σ(θ2Tvc))
= σ ( θ 0 T v c ) σ ( θ 1 T v c ) σ ( − θ 2 T v c ) =\sigma\left(\theta_{0}^{T} v_{c}\right) \sigma\left(\theta_{1}^{T} v_{c}\right) \sigma\left(-\theta_{2}^{T} v_{c}\right) =σ(θ0Tvc)σ(θ1Tvc)σ(−θ2Tvc)
上面公式中有 ( 1 − σ ( θ 2 T v c ) ) = σ ( − θ 2 T v c ) \left(1-\sigma\left(\theta_{2}^{T} v_{c}\right)\right)=\sigma\left(-\theta_{2}^{T} v_{c}\right) (1−σ(θ2Tvc))=σ(−θ2Tvc),这里是通过对sigmoid函数进行转化得到的,也就是 σ ( − x ) = 1 − σ ( x ) \sigma(-x)=1-\sigma(x) σ(−x)=1−σ(x)。
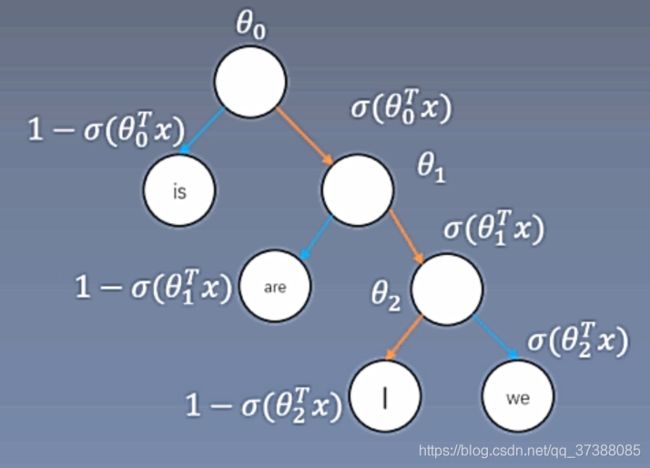
如下图,假设 L ( w ) L(w) L(w)为从二叉树的根节点到词w的叶节点的路径(包括根节点和叶节点)上的节点数。设 n ( w , j ) n(w,j) n(w,j)为该路径上第j个结点,并设该结点的背景词向量为 u n ( w , j ) u_{n(w,j)} un(w,j)。如下图中的词 w 3 w_3 w3的 L ( w 3 ) = 4 L(w_3)=4 L(w3)=4。层次softmax将跳字模型中的条件概率近似表示为:
p ( w ∣ w I ) = ∏ j = 1 L ( w ) − 1 σ ( [ n ( w , j + 1 ) = = ch ( n ( w , j ) ) ] ⋅ v n ( w , j ) ⊤ v w I ) p\left(w \mid w_{I}\right)=\prod_{j=1}^{L(w)-1} \sigma\left([n(w, j+1)==\operatorname{ch}(n(w, j))] \cdot v_{n(w, j)}^{\top} v_{w_{I}}\right) p(w∣wI)=j=1∏L(w)−1σ([n(w,j+1)==ch(n(w,j))]⋅vn(w,j)⊤vwI)

公式中的 σ \sigma σ函数与sigmoid激活函数的定义相同,leftChild(n)是结点n的左子结点:如果判断x为真,公式中的[x]=1,否则[x]=-1。我们计算一下上图中给定中心词 w c w_c wc生成背景词 w 3 w_3 w3的条件概率。我们需要将 w c w_c wc的词向量 v c v_c vc和根节点到 w 3 w_3 w3路径上的非叶子结点向量一一求内积。由于在二叉树中由根结点到叶结点 w 3 w_3 w3的路径上需要向左、向右再向左遍历看,我们得到:
P ( w 3 ∣ w c ) = σ ( u n ( w 3 , 1 ) ⊤ v c ) ⋅ σ ( − u n ( w 3 , 2 ) ⊤ v c ) ⋅ σ ( u n ( w 3 , 3 ) ⊤ v c ) P\left(w_{3} \mid w_{c}\right)=\sigma\left(\boldsymbol{u}_{n\left(w_{3}, 1\right)}^{\top} \boldsymbol{v}_{c}\right) \cdot \sigma\left(-\boldsymbol{u}_{n\left(w_{3}, 2\right)}^{\top} \boldsymbol{v}_{c}\right) \cdot \sigma\left(\boldsymbol{u}_{n\left(\mathfrak{w}_{3}, 3\right)}^{\top} \boldsymbol{v}_{c}\right) P(w3∣wc)=σ(un(w3,1)⊤vc)⋅σ(−un(w3,2)⊤vc)⋅σ(un(w3,3)⊤vc)
由于 σ ( x ) + σ ( − x ) = 1 \sigma(x)+\sigma(-x)=1 σ(x)+σ(−x)=1,给定中心词 w c w_c wc生成词典V中任一词的条件概率之和为1这一条件也将满足:
∑ w ∈ V P ( w ∣ w c ) = 1 \sum_{w \in V} P\left(w \mid w_{c}\right)=1 w∈V∑P(w∣wc)=1
综上,当词典V很大时,层次softmax训练中每一步的梯度计算开销相较未使用近似训练时大幅降低。
2.2 负采样
softmax计算开销大,是因为每一步的梯度计算都包含字典大小数目的项的累加,为了降低复杂度,负采样舍弃了softmax多分类,将多分类变为一个二分类。
将一个多分类变为二分类,我们需要有正样本和负样本。以跳字模型为例,将中心词和背景词一起出现作为正样本,也就是将背景词 w o w_o wo出现在中心词 w c w_c wc的背景窗口看做一个事件,并将该事件的概率计算为:
P ( D = 1 ∣ w c , w o ) = σ ( u o ⊤ v c ) P\left(D=1 \mid w_{c}, w_{o}\right)=\sigma\left(\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}\right) P(D=1∣wc,wo)=σ(uo⊤vc)
对于模型来说,上述事件的概率越大越好。负采样通过采样获得负样本,负采样根据分布 P ( w ) P(w) P(w)采样K个未出现在背景窗口中的词,即噪声词(这样虽然有可能随机采样到背景词,但是当词表很大时,采样得到背景词的概率很小,因此忽略此影响)。注意对于每个正样本,不能只采样一个负样本,因为可能会出现偏差,因为正样本是真实的,而负样本是采样得到的,所以一般情况下会采样K个负样本(一般是3-10个)。每个负样本出现的概率为:
P ( D = 1 ∣ w c , w k ) = σ ( u k ⊤ v c ) P\left(D=1 \mid w_{c}, w_{k}\right)=\sigma\left(\boldsymbol{u}_{k}^{\top} \boldsymbol{v}_{c}\right) P(D=1∣wc,wk)=σ(uk⊤vc)
通过负采样,每一个正样本都有对应的K个负样本,我们的目的是增加正样本出现的概率,降低负样本出现的概率。负采样得到的似然函数可以表示为:
∏ i = 1 T ∏ − m ⩽ j ⩽ m , j ∗ 0 P ( w ( t + j ) ∣ w ( t ) ) \prod_{i=1}^{T} \prod_{-m \leqslant j \leqslant m, j * 0} P\left(w^{(t+j)} \mid w^{(t)}\right) i=1∏T−m⩽j⩽m,j∗0∏P(w(t+j)∣w(t))
上述公式中的条件概率被近似为:
P ( w ( t + j ) ∣ w ( t ) ) = P ( D = 1 ∣ w ( t ) , w ( t + j ) ) ∏ k = 1 , w k ∼ P ( w ) K ( 1 − P ( D = 1 ∣ w ( t ) , w k ) ) P\left(w^{(t+j)} \mid w^{(t)}\right)=P\left(D=1 \mid w^{(t)}, w^{(t+j)}\right) \prod_{k=1, w_{k} \sim P(w)}^{K} \left(1-P\left(D=1 \mid w^{(t)}, w_{k}\right)\right) P(w(t+j)∣w(t))=P(D=1∣w(t),w(t+j))k=1,wk∼P(w)∏K(1−P(D=1∣w(t),wk))
设文本序列中时间步t的词 w ( t ) w^{(t)} w(t)在词典中的索引为 i t i_t it,噪声词 w k w_k wk在词典中的索引为 h k h_k hk。有关以上条件概率的对数损失为:
− log P ( w ( t + ȷ ) ∣ w ( t ) ) = − log P ( D = 1 ∣ w ( t ) , w ( t + j ) ) − ∑ k = 1 , w k ∼ P ( w ) K log ( 1 − P ( D = 1 ∣ w ( l ) , w k ) ) -\log P\left(w^{(t+\jmath)} \mid w^{(t)}\right)=-\log P\left(D=1 \mid w^{(t)}, w^{(t+j)}\right)-\sum_{k=1, w_{k} \sim P(w)}^{K} \log \left(1-P\left(D=1 \mid w^{(l)}, w_{k}\right)\right) −logP(w(t+ȷ)∣w(t))=−logP(D=1∣w(t),w(t+j))−k=1,wk∼P(w)∑Klog(1−P(D=1∣w(l),wk))
= − log σ ( u i t + j ⊤ v i t ) − ∑ k = 1 , w k ∼ P ( w ) K log ( 1 − σ ( u h k ⊤ v i t ) ) =-\log \sigma\left(\boldsymbol{u}_{i_{{t+j}}}^{\top} \boldsymbol{v}_{i_{t}}\right)-\sum_{k=1, w_{k} \sim P(w)}^{K} \log \left(1-\sigma\left(\boldsymbol{u}_{h_{k}}^{\top} \boldsymbol{v}_{i_{t}}\right)\right) =−logσ(uit+j⊤vit)−k=1,wk∼P(w)∑Klog(1−σ(uhk⊤vit))
= − log σ ( u i t + j ⊤ v i t ) − ∑ k = 1 , w k ∼ P ( w ) K log σ ( − u h k ⊤ v i t ) =-\log \sigma\left(u_{i_{t+j}}^{\top} v_{i_{t}}\right)-\sum_{k=1, w_{k} \sim P(w)}^{K} \log \sigma\left(-u_{h_{k}}^{\top} v_{i_{t}}\right) =−logσ(uit+j⊤vit)−k=1,wk∼P(w)∑Klogσ(−uhk⊤vit)
现在训练中每一步的梯度计算开销不再与词典大小相关,而与K线性相关。当K取较小的常数时,负采样每一步的梯度计算较小。
2.2.1 负采样原理
P ( w ) = U ( w ) 3 4 Z P(w)=\frac{U(w)^{\frac{3}{4}}}{Z} P(w)=ZU(w)43
上述公式中的 U ( w ) U(w) U(w)是词w的词频,Z是归一化参数,使得求解之后的概率依旧为1;举个例子,词库中有两个词a和b,其中 U ( a ) = 0.01 U(a)=0.01 U(a)=0.01, U ( b ) = 0.99 U(b)=0.99 U(b)=0.99。则词a的采样频率为
P ( a ) = 0.01 ∗ ∗ 0.75 0.01 ∗ ∗ 0.75 + 0.99 ∗ 0.75 = 0.03 P(a)=\frac{0.01 * * 0.75}{0.01 * * 0.75+0.99 * 0.75}=0.03 P(a)=0.01∗∗0.75+0.99∗0.750.01∗∗0.75=0.03
P ( a ) = 0.99 ∗ ∗ 0.75 0.01 ∗ ∗ 0.75 + 0.99 ∗ 0.75 = 0.97 P(a)=\frac{0.99 * * 0.75}{0.01 * * 0.75+0.99 * 0.75}=0.97 P(a)=0.01∗∗0.75+0.99∗0.750.99∗∗0.75=0.97
这样可以减少频率大的词的抽样概率,增加频率小的词的抽样概率;这是因为一些重要的词出现的概率比较小,一些不重要的词比如the出现的概率比较大,通过上述采样方法,可以提高出现频率小的词被采样到的概率。
总结一下层数softmax和负采样的关系,层次softmax基本思想是将softmax转化为多个sigmoid,通过这种方式可以大规模较少计算量;负采样是将一个多分类问题转换成二分类问题,也相当于将softmax转化为sigmoid。
2.3 重采样(二次采样)
文本数据中一般会出现一些高频词,如英文中的“the”“a”和“in”等。通常来说,在一个背景窗口中,一个词(如“chip”)和较低频率词(如“microprocessor”)同时出现比和较高频词(如“the”)同时出现对训练词嵌入模型更有效。因此在训练词嵌入模型时可以对词进行二次采样。具体来说,数据集中每个被索引词 w i w_i wi将有一定概率被丢弃,该丢弃概率为
P ( w i ) = m a x ( 1 − t f ( w i ) , 0 ) P\left(w_{i}\right)=max\left(1-\sqrt{\frac{t}{f\left(w_{i}\right)}},0\right) P(wi)=max(1−f(wi)t,0)
其中 f ( w i ) f(w_i) f(wi)是数据集中词 w i w_i wi的个数与总词数之比,常数t是一个超参数(实验中设置为 1 0 − 4 10^{-4} 10−4)。可见,只有当 f ( w i ) > t f(w_i)>t f(wi)>t时,我们才有可能在二次采样中丢弃词 w i w_i wi,并且越高频的词被丢弃的概率越大。
具体实现就是我们随机生成一个0-1之间的随机数,如果这个随机数的值小于 P ( w i ) P(w_i) P(wi),则该词会被丢弃。
2.4 word2vec关键技术总结
word2vec主要包括两种模型,分别为跳字模型和连续词袋模型,其中跳字模型是用中心词预测背景词,而连续词袋模型是用背景词预测中心词。word2vec有两种加速训练的方法,分别为负采样和层次softmax,负采样将一个多分类问题转化为二分类问题,其中一个正样本是由一对背景词和中心词组成,负样本是由一对中心词和随机采样得到的词组成,层次softmax使用哈夫曼树构建一个二叉树,将softmax转换为多个sigmoid,简化运算。还有一个技术就是重采样或者说是二次采样,该方法会随机将一些高频词丢弃。
3.模型复杂度
3.1 模型复杂度的概念
论文中给出了模型复杂度的概念:
O = E × T × Q O=E \times T \times Q O=E×T×Q
- O是训练复杂度;
- E是训练迭代次数;
- T是数据集大小;
- Q是模型计算复杂度;
简单来说,E代表要训练多少轮,T代表每一轮要训练多少次,Q代表每一次训练多长时间,总的时间复杂度就是三者相乘。对于不同模型,E和T是一样的,所以我们只需要比较Q。论文中求Q的方法比较特殊,论文使用参数的数目来替代时间复杂度,也就是说一次计算需要求解的参数数量来代替模型复杂度。
3.2 NNLM模型复杂度
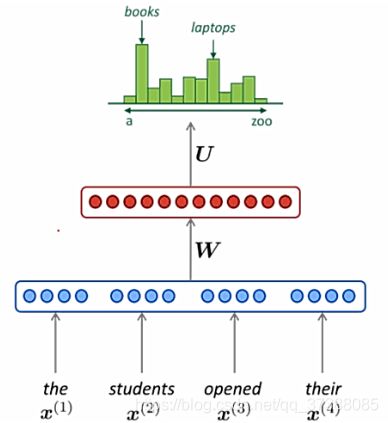
Q = V ∗ H + N ∗ D ∗ H + N ∗ D Q = V*H + N*D*H + N*D Q=V∗H+N∗D∗H+N∗D
公式中的N是指输入的N个上文词(用前N个词预测下一个词,所以输入层是N*D个参数),D表示每个词的词向量维度,V代表词表的大小,H是隐藏层的大小;
输入层到隐藏层是全连接,输入层的维度为 N ∗ D N*D N∗D,隐藏层的维度为H,所以输入层到隐藏层的W的参数数量为 N ∗ D ∗ H N*D*H N∗D∗H,隐藏层到输出层是一个全连接层,隐藏层的维度为H,输出层使用到softmax计算词典中每个词的概率,所以输出层的维度是词表的大小,所以隐藏层到输出层的参数矩阵为 V ∗ H V*H V∗H。
NNLM的输出层也可以使用层次softmax,这样隐藏层到输出层的参数矩阵可以表示为 H ∗ l g V H*lgV H∗lgV。
3.3 RNNLM模型复杂度

这里使用D表示每个词的维度,隐藏层的维度为H,则w(t)的参数数量为 1 ∗ D 1*D 1∗D,输入层到隐藏层的参数矩阵的参数数量为 D ∗ H D*H D∗H,s(t-1)是上一个隐藏层的输出,上一个隐藏层的输出与当前隐藏层的参数矩阵的参数数量为 H ∗ H H*H H∗H,输出层的维度为词表的数量,所以隐藏层到输出层的参数矩阵的参数数量为 H ∗ V H*V H∗V,RNNLM的输出层同样可以使用层次softmax,所以隐藏层到输出层的参数数量可以表示为 H ∗ l g V H*lgV H∗lgV
所以RNNLM的模型复杂度为:
O = 1 ∗ D + D ∗ H + H ∗ H + H ∗ V O = 1*D + D*H + H*H + H*V O=1∗D+D∗H+H∗H+H∗V
按论文中的说法,D和H的维度是一样的,因此公式中的 1 ∗ D + D ∗ H + H ∗ H 1*D + D*H + H*H 1∗D+D∗H+H∗H可以表示为 H ( 1 + 2 H ) H(1+2H) H(1+2H),可以常数项消去得到 H ∗ H H*H H∗H,这样可以得到化简后的模型复杂度 O = H ∗ H + V ∗ H O = H*H + V*H O=H∗H+V∗H
3.4 Skip-Gram模型复杂度
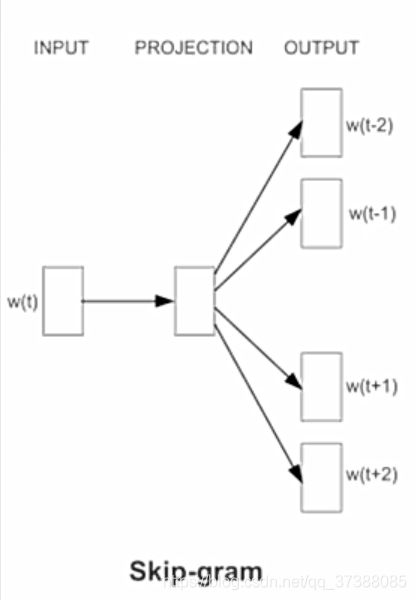
跳字模型,输入是一个中心词,设每个词的维度为D,词表大小为V,则输入的参数数量为 1 ∗ D 1*D 1∗D,投影层的维度为 D ∗ V D*V D∗V,通过softmax得到输出每个词的概率,这里同样可以使用层次softmax简化运算,这样投影层到输出的参数矩阵为 D ∗ l g 2 D*lg2 D∗lg2。因为要基于中心词计算C个背景词,因此上述操作需要重复C词。所以跳字模型的复杂度为:
Q = C ( D + D ∗ V ) Q=C(D+D*V) Q=C(D+D∗V)
如果跳字模型使用层次softmax,则模型复杂度变为:
Q + C ( D + D ∗ l g V Q+C(D+D*lgV Q+C(D+D∗lgV
对于使用负采样的跳字模型,则模型的复杂度为:
Q = C ( D + D ∗ ( K + ! ) ) Q=C(D+D*(K+!)) Q=C(D+D∗(K+!))
公式中的K是负样本个数,1指的是正样本,对于每一个正样本都有K个负样本,因此投影层到输出层的矩阵参数数量为 D ∗ ( K + 1 ) D*(K+1) D∗(K+1)。
3.5 CBOW模型复杂度
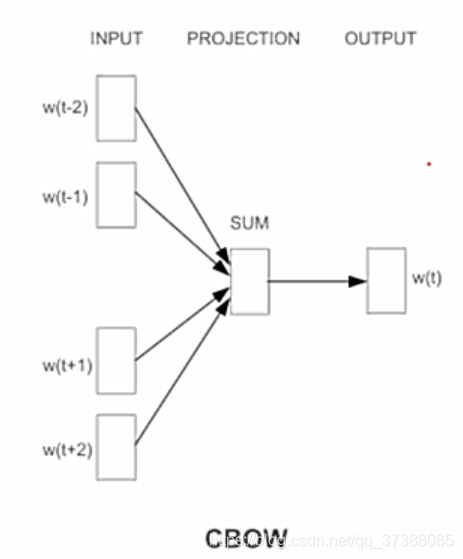
原始的CBOW模型的输入需要N个背景词,每个背景词的维度为D,因此输入的参数数量为 N ∗ D N*D N∗D,然后输入的N个词进行平均操作之后得到一个D维的向量,投影层到输出层需要一个softmax操作,因此参数矩阵的参数数量为 D ∗ V D*V D∗V,所以CBOW模型的原始模型复杂度为:
Q = N ∗ D + D ∗ V Q=N*D+D*V Q=N∗D+D∗V
和跳字模型类似,使用层序softmax之后CBOW的模型复杂度为:
Q = N ∗ D + D ∗ l g V Q=N*D+D*lgV Q=N∗D+D∗lgV
使用负采样之后得到的CBOW模型复杂度为:
Q = N ∗ D + D ∗ ( K + 1 ) Q=N*D+D*(K+1) Q=N∗D+D∗(K+1)
3.6 模型复杂度对比
前馈神经网络NNLM:
Q = N ∗ D + N ∗ D ∗ H + H ∗ log 2 V Q=N * D+N * D * H+H * \log _{2} V Q=N∗D+N∗D∗H+H∗log2V
循环神经网络RNNLM:
Q = H ∗ H + H ∗ log 2 V Q=H * H+H * \log _{2} V Q=H∗H+H∗log2V
CBOW+层次softmax:
Q = N ∗ D + D ∗ log 2 V Q=N * D+D * \log _{2} V Q=N∗D+D∗log2V
Skip-Gram+层次softmax:
Q = C ( D + D ∗ log 2 V ) Q=C\left(D+D * \log _{2} V\right) Q=C(D+D∗log2V)
CBOW+负采样:
Q = N ∗ D + D ∗ ( K + 1 ) ) Q=N * D+D *(K+1)) Q=N∗D+D∗(K+1))
Skip-Gram+负采样:
Q = C ( D + D ∗ ( K + 1 ) ) Q=C(D+D *(K+1)) Q=C(D+D∗(K+1))
4.实验和结果——介绍论文中的模型的实验设置和运行结果
对于词向量好坏的评测,业界最常用的最快的评测方式是计算词之间的相似度任务和与之相关的词汇类比任务,这两个方法都是内部评价方法。
- 相似度任务(word similarity task)
- 相似度任务,目的是评估词向量模型在两个词之间的语义紧密度和相关性能力。比如说男人和女人,男孩和女孩,中国和北京等这些词段之间的相似度。
- 评价指标:斯皮尔曼等级相关系数,衡量两个变量的依赖性指标,利用单调方程评价两个统计变量的相关性,如果数据中没有重复值,并且两个变量x和y完全是单调相关的,斯皮尔曼相关系数就为+1或者-1。也就是说,绝对值越接近1,相似度就越大。 ρ = ∑ i ( x i − x ˉ ) ( y i − y ˉ ) ∑ i ( x i − x ˉ ) 2 ∑ i ( y i − y ˉ ) 2 \rho =\frac{\sum_i(x_i-\bar{x})(y_i-\bar {y})}{\sqrt{\sum_i(x_i-\bar {x})^2 \sum_i(y_i-\bar{y})^2}} ρ=∑i(xi−xˉ)2∑i(yi−yˉ)2∑i(xi−xˉ)(yi−yˉ)
- 词汇类比任务(word analogy task)
- 词汇类比任务,考察了用词向量来推断不同单词之间的语义关系的能力。在这个任务中,假如有3个单词A,B,S已经给出,目标就是判断出第四个单词T能满足在A与B相似的基础上推断出T和S也是相似的。可以根据矢量的加减做到这一点,因为word2vec生成的词向量在空间上具有特定的关系,比如说希望从向量空间上求一个向量,这个向量到罗马的向量空间距离就等于法国减去巴黎的空间向量距离。
- vec(法国) - vec(巴黎) = answer_vector - vec(罗马)
- answer_vector = vec(法国) - vec(巴黎) + vec(罗马)
这两个任务的评测脚本一般都能在网上找到,近两年来词向量仅仅在这两个任务上进行评测已经不能得到公认了。要想得到公认,词向量的好坏需要应用到具体的任务中进行评测,包括句子分类,文本分类,命名体识别等任务中,这些任务就是外部任务。但是这两个任务是最基本的评测方式,论文中也进行了这部分的实验。
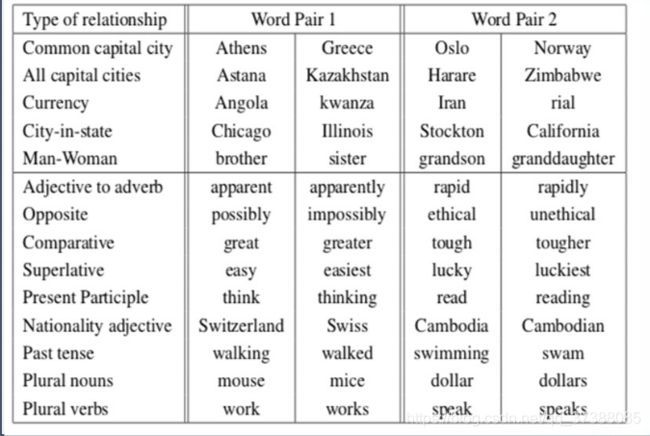
在论文中,为了进行实验,论文定义了一个复杂的测试集,包括了五种语义问题以及九个类型的语法问题,图中展示的就是每个类别的两个样本集的展示。例如在语义问题上有国家的首都,雅典和希腊就是一个词对。还有美国的州府,芝加哥和伊利诺伊就是一个词对。还有性别,比如说哥哥和妹妹等等。
在语法的问题上,也规定了词的形态,有反义词,比较级,最高级等等。
制作这个测试集的原因是作者想在实验结果中更好地展示模型的有效性。
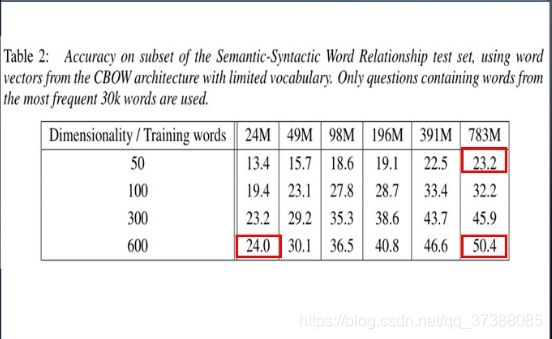
实验首先利用了训练数据的子集进行训练,评价各种模型。把单词表限制在频率最高的三万个单词当中。看一下使用连续词袋模型得到的一些结果。行代表语料库的大小,列表示词向量的维度。可以看到随着词向量维度的增加以及语料库单词的增多,模型的准确率是越来越好的。当语料中有783M单词的时候,词向量如果取600维,准确率达到实验表中最高的50.4%,这也就意味着在训练词向量的过程中要使用相对大的数据集和较高的维度训练。但是增加二者也意味着运算量的增加。
接着看一下不同模型的比较,下图展示了论文的改进模型都是优于之前的模型的。可以看到在相同的语料(783M)和词向量的维度(300)的条件下,跳字模型在语义下(semeantic)表现比较出色,在语法下(syntactic)相对也很好,准确率都能到达50%以上。连续词袋模型在语法下表现不错,但是还是弱于跳字模型,在语义上表现非常糟糕。

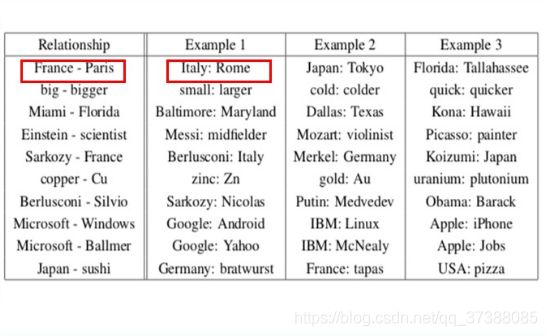
接着看一下使用DistBelief分布式框架训练的模型的比较,在大规模语料上,通过使用NNLM,也就是神经网络语言模型训练高维度的词向量基本上是不可能的,成本太高,图中显示训练100维的词向量需要14天和180个CPU支持。但是word2vec模型不需要那么多的计算资源。而且在大规模语料加高强度的情况下,连续词袋模型在语义上的表现开始并不弱于跳字模型了。
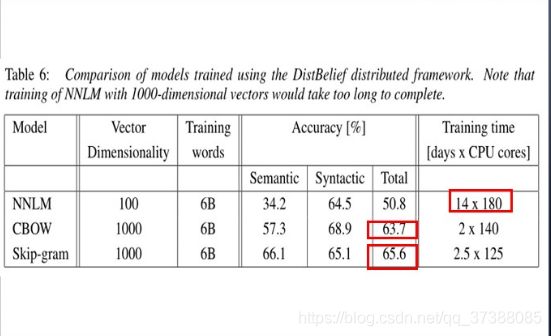
接下来看一下模型学习到的关系示例,图中展示了符合各种各样关系的单词对,依照之前提到的词汇类比任务,通过两个单词的向量加减来定义单词之间的关系。例如vec(Pairs) - vec(France) + vec(Italy) = vec(Rome)。最后用这种方法得到许多类似于这样的单词对,可以看出,准确率是相当高的,在大规模的预料库中可能会得到更好的结果。
5.讨论和结论
超参数选择:
请问,利用genism做word2vec的时候,词向量的维度和单词数目有没有一个比较好的对照范围呢?
- dim一般在100-500之间选择;
- dim初始值为词典V的大小的1/4次方,例如V=10k,dim=100;
- 在训练词向量的时候忽略出现频率小于min_count的词,min_count一般在2-10之间选择;
word2vec存在的问题:
- 对每个局部上下文窗口单独训练,没有利用包含在全局共现矩阵中的统计信息;
- 假如给定一个单词apple,怎么确定是水果apple还是苹果公司呢?对多义词无法很好的表示和处理,因为使用了唯一的词向量。只用一个固定的词向量来做这些表达显然是不合理的。所以有研究人员在之后的研究中提取出了其它的一些词向量处理方式glove;
- glove,利用全局信息编码词向量
总结——论文创新点
- 提出了两种从大规模数据集中计算连续向量表示的模型,简化了结构,大大减小了计算量,从而可以使用更高维度,更大的数据量;
- 能在较少的资源上进行运算;
- 在大规模语料上得到高质量的词向量;
- 论文使用的分层softmax和负采样在开篇阶段引入的论文里有介绍,想了解的可以看论文。