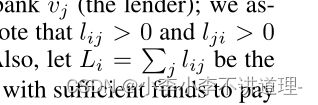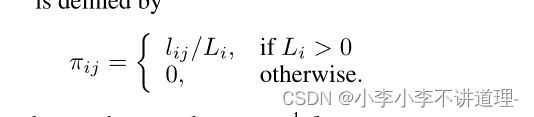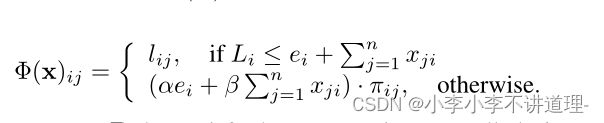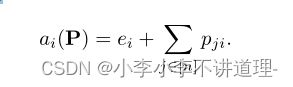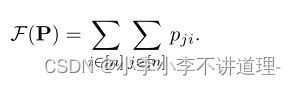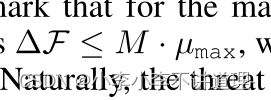论文2：Forgiving Debt in Financial Network Games

目录

​编辑

1.摘要  

2.结论

3.介绍

 4.工作

最优现金注入

---

1.摘要  

        金融系统由网络表示，其中节点对应于银行，有向标记边对应于银行之间的债务合约。一旦确定了付款时间表，我们假设如果银行有足够的资金，银行不能拒绝向其贷方之一付款，则系统的流动性被定义为网络中支付的总和。最大化系统流动性是任何金融当局的自然目标，因此，我们研究金融当局向某些银行提供救助资金或免除其他银行的债务以最大化流动性的环境，并研究实现这一目标的有效方法. 我们研究了贪婪救助政策与最优救助政策相比的近似比率，并且我们分别研究了寻找最优债务消除和预算约束最优救助政策的计算难度。我、们还从博弈论的角度研究金融系统。我们观察到，如果这有助于其中一个借款人保持偿付能力并避免与违约相关的成本，那么消除一些新债务可能符合银行的最佳利益。假设银行的福利（即效用）与他们从网络收到的收款一致，我们定义并分析了希望通过战略性地放弃一些收款来最大化其效用的银行之间的博弈。此外，我们通过考虑救助付款来扩展之前的游戏。在正式定义上述博弈之后，我们证明了纯纳什均衡的存在性和质量。

2.结论

贡献

1.金融当局通过注入资金或消除债务来最大化网络中的流动性。

2.银行通过对贷款人免除一些债务，来获得更大的效益。

3.分析博弈与那什均衡的性质。

4.引入了the Effect of Anarchy（无政府效应）的概念，将初始网络中的流动性与最差纳什均衡(分别为最佳纳什均衡)中的流动性进行比较。

未解决的问题：

1.考虑到一些优化问题的计算难度，考虑近似算法是有意义的。

2.从博弈论的角度来看，也可以 从机构设计的角度考虑问题，在银行薄弱的情况下设计激励兼容的政策来保留所有即将到来的负债。

3.介绍

网络：显示银行之间的负债的相互关系，节点对应银行，边对应负债关系。

银行总资产：外部资产和收入

违约：银行资产不足以覆盖其负债，资产价值将减少。

三个原则偿还债务：

        1.绝对优先原则：资产充足的银行必须全额支付其负债

        2.有限责任原则：资产不足以偿还负债的银行将违约，将所有资产支付给贷方。

        3.比例性：在违约情况下，向贷方支付的款项按各自的债务比例支付。

        满足上述支付的称为清算支付和最大清算支付

衡量系统健康程度的一个自然指标：一个金融网络的总流动性是通过清算时支付的总和来衡量。

研究：研究金融监管机构对选定的银行进行救助、免除债务的可能性，目的最大化系统流动性。

金融当局，也就是政府或者其他监管机构，通过干预介入希望保持流动性尽可能高。消除债务可以对系统流动性产生积极的影响，因为借款人因为撤销债务而避免了违约成本，使资金流动增加。

 定义一个game：在金融网络上进行边缘去除，其中银行作为agent，她希望最大化她们的总资产，并且可能有意放弃一部分应得的收入来实现这一目标。

我们的贡献：

1.当监管机构可以适当地消除债务或注入资金来修改网络时，考虑如何最大化系统流动性相关的计算问题。

2.考虑game，agent选择免除一些债务来获取更大的利益

3.通过求解线性规划，给出了在无违约成本的多项式时间内如何计算最优现金注入策略。当面对比较多的违约成本时，这是一个NP难问题。

4.基于LP算法（线性规划）需要用可预算的知识，研究了贪婪现金注入策略的近似比，对于债务去除，我们证明了找到去除后使系统流动性最大化的债务集是np困难的，相关的优化问题也是np困难的。

4.对于边缘去除博弈，无论是否有机构注入资金，我们研究了纳什均衡的存在性和质量，同时也解决了计算复杂度问题。

5.除了“Price of Anarchy”  和 "Price of Stability"这些公认 的概念，本文还引入“Effect of Anarchy” ，作为衡量均衡质量的新指标。

在一个game中，全局最优解，一般来说不可能达到，一般都是达到纳什均衡解，均衡解可能不止一个，也有好有坏，那么为了反映这个纳什均衡的解的情况到底好不好，好到什么程度？坏到什么程度？就有学者提出了POA和POS。

POA等于这个game中的全局最优解 比 纳什均衡解中的最小值，也就是说，POA越大，意味着纳什均衡解中差的那一面越差。

POS等于这个game中的全局最优解 比 纳什均衡解中的最大值，POS越接近1，代表这个纳什均衡解好的那一面越好

纳什均衡（Nash equilibrium），又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果任意一位参与者在其他所有参与者的策略确定的情况下，其选择的策略是最优的，那么这个组合就被定义为纳什均衡。

一个策略组合被称为纳什均衡，当每个博弈者的均衡策略都是为了达到自己期望收益的最大值，与此同时，其他所有博弈者也遵循这样的策略。

金融网络由A financial network N = (V, E)表示，其中V代表所有银行的集合，E代表包含银行之间的有向边，

Lij表示vi（借款人）对vj（贷款人）借的钱。

银行总负债：

相对负债矩阵：

Pij表示表示vi到vj的实际支付，银行Vi对外的支付总额：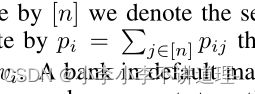

违约的银行可能需要清算其他违约成本，这里定义为α，β∈【0,1】，为违约成本建模，

 Given clearing payments P（清算款项P）:定义银行Vi的总资产为外部资产加上流入款项的总和。

 Manimal clearing payments(最大清算支付）： [Eisenberg and Noe, 2001; Rogers and V er-
aart, 2013]提出在多项式时间内计算，

通过测验系统的总流动性F(P)作为网络的支付总和：

 

 监管机构对银行的 threat index μ：威胁指数（自己理解为影响因子），代表监管机构向Vi银行注入一笔资金，用该参数来衡量总流动性的变化多少，一个单位的现金代表足够下的金额，因此现金注入后，所有违约银行将不会发送任何变化。我们注意到，对于总流动性来说：大

μmax为最大威胁指数，也就是有偿付能力的银行为0，违约银行的至少为1

 

  是所有的违约银行集合，因为L代表该银行的所有负债，α代表该银行的总资产。

“威胁指数”一词旨在捕捉银行现金流减少甚至银行违约对网络构成的“威胁”;该指数可以被认为是计算了所有违约债权人，这些违约债权人将在该银行的潜在违约后出现。

 总结：

 4.工作

最优现金注入

 第一种情况：不考虑违约成本

定理1 ：最优现金注入策略的计算可在多项式时间内计算

由于最优策略的一些缺点：现金注入并不是单调的，基于LP的算法非常依赖于可用预算的知识。

为了缓解这些特性：将注意力转移到贪婪算法上

最优债务免除

定理4：计算去除边缘集的使系统流动性最大化的问题是np困难的。

定理5：在有违约代价的网络中，以下三个问题是NP-hard。计算一个边缘集，它的消除:a)确保系统偿付能力和最大化系统流动性，b)确保系统偿付能力和最小化删除的负债数额，c)保证给定代理不再违约和最小化删除的负债数额。

 纳什均衡（Nash equilibrium），又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果任意一位参与者在其他所有参与者的策略确定的情况下，其选择的策略是最优的，那么这个组合就被定义为纳什均衡。

一个策略组合被称为纳什均衡，当每个博弈者的均衡策略都是为了达到自己期望收益的最大值，与此同时，其他所有博弈者也遵循这样的策略。

Effect of Anarchy   EoA:衡量原始网络（不去除边）的系统流动性与最好最坏纳什均衡之间的差异

结论：

本文研究了边缘移动博弈中纳什均衡的存在性和质量，同时我们也解决了在违约成本和/或现金注入是否适用的不同假设下的计算复杂性问题。我们对边缘去除博弈的无政府效应的研究结果表明，令人惊讶的是，在存在违约成本的情况下，即使最糟糕的纳什均衡在流动性方面也可以任意优于原始网络。然而，在没有违约成本的情况下，情况发生了逆转，我们观察到，就流动性而言，原始网络可能比最差均衡要好得多;这与《无政府价格》的类似结果是一致的。我们从基本情况的一些结果开始，即没有违约成本;回想一下，对于α = β = 1的保持结果，我们在报表中没有提及违约成本。

我们的第一个结果利用了这样一个事实:对于没有现金注入的边去除游戏，保留所有边的策略轮廓是一个(不一定是唯一的)纳什均衡。

定理6。没有现金注入的边缘消除博弈总是承认纳什均衡。

定理7。在没有现金注入的边缘去除游戏中，混乱效应是无界的，稳定效应最多为1。

我们的下一个结果表明，一旦我们允许现金注入，纳什均衡可能不存在。

定理8。有一个带现金注入的去边博弈不承认纳什均衡。

定理9。在边缘消除游戏中(是否有现金注入)，稳定的代价是无限的。

定理10。在现金注入的边缘去除游戏中，无政府状态的影响至少是n−1。

定理11。现金注入的去边博弈的稳定性效应为Ω(n)。

我们现在提出了一系列的结果，在违约成本存在，但不允许现金注入的情况下。与既没有违约成本也没有现金注入的情况相反，我们表明纳什均衡不再保证存在;下一个结果是定理8的补充。

定理12。有一种有违约成本但没有现金注入的去边博弈不承认纳什均衡。

然而，对于某些受限拓扑，纳什均衡的存在是有保证的;特别是，保持所有边都是纳什均衡。

定理13。如果金融网络是一棵树或一个循环，有违约成本但没有现金注入的去边博弈总是承认纳什均衡

引理1。有违约成本但没有现金注入的边去博弈满足以下条件:给定任何网络和任何战略轮廓，任何单方面的边去，只会微弱地提高相应银行的总资产，也会微弱地提高网络中其他所有银行的总资产。因此，系统的总流动性增加了

事实上，即使是最坏的纳什均衡的系统流动性也可以任意高于原始网络。

要明白这一点，考虑定理14证明中的网络，该定理承认一个唯一的纳什均衡，其总流动性任意高于原始网络。

定理14。当存在违约成本但没有现金注入时，稳定性效应任意地接近于0。

定理15。在有违约成本的边缘消除博弈中，以下问题是np困难的:a)确定纳什均衡是否存在，b)计算纳什均衡，当纳什均衡保证存在时，c)计算最佳对策策略，d)计算使系统流动性最大化的策略轮廓。