XGB(有监督学习)和多维时序模型结合——预测风电出力

新能源风力发电机上保存有很多实时传感器的感应数据。

解决的问题：

1，想要通过传感器数据预测未来一段时间出力功率。

2，单XGB等有监督的机器学习模型，根据输入感应器数据预测出力功率，有一个问题，是用不了预测时间段的传感器参数数据（因为预测时间段的数据没有发生）。

3，时序模型，可以对某一列传感器数据预测未来一段时间的值。

4，通过时序模型对多维度的传感器数据都预测出未来值，使用这个未来值作为XBG(有监督学的输入)更好的预测出风电机出力功率。

在之后的研究中发现对于不稳定维度数据，该方法有奇效，在后文说明。

目录

解决的问题：

数据说明

数据指标介绍

 算法内容

数据分析，维度稳定性评估

时序预测模型

时序模型重新构建数据集

Xgb+时序模型预测数据集

结果输出：

结论点：

---

数据说明

数据是百度平台举办比赛，开源出来的数据：

清洗后的数据和源码链接：

链接：https://pan.baidu.com/s/1JDoHgp-9cXmt72X5lm1d4w?pwd=w1xz 
提取码：w1xz 
且用且珍惜！！

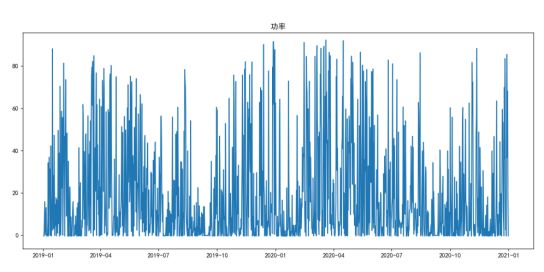
数据来自风电场及光伏电站的实际出力数据，运行记录数据、实测气象数据以及数值天气预报生成的场站气象预测报数据，考虑了实际电网运行中可能遇到的检修、故障以及限电场景，选取的风电场及光伏电站分布于华北、华中、西北等区域，覆盖戈壁、山地、内陆平原、丘陵、海上及山地和高原叠加等多种地形。

数据集包括 27 个新能源场站（14 个风电场、13 个光伏电站）2019 年、2020 年两年的历史出力数据、运行记录数据、实测气象数据以及天气预报数据。数据集命名为 dataset 文件夹，文件夹中包括场站基本信息汇总表、各场站运行数据、运行记录数据、气象预测数据。参赛者根据数据集自行拆分训练集和验证集。

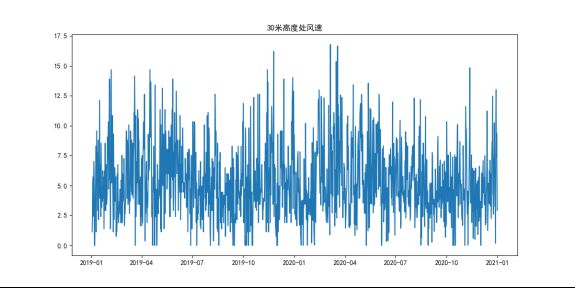
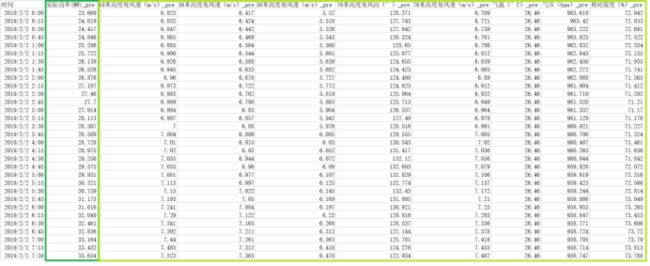
场站基本信息包括场站名称，额定容量，发电单元型号，发电单元数量及扩容信息。厂站出力表含时间（北京时间）和实际功率，时间步长为 15 分钟。测风数据包括 10 米高度处风速、10 米高度处风向、30 米高度处风速、30 米高度处风向、50 米高度处风速、50 米高度处风向、70 米高度处风速、70 米高度处风向、风机轮毂高度处风速、风机轮毂高度处风向、气温、气压、相对湿度等数据我们基本上使用的就是这些数据。

还有些气象数据（表头Y_前缀）起报时间（UTC）、预报时间（UTC）、30 米温度、动量通量、30 风向、100 米风速、70 米风速、30 米风速、10 米风速、100 米风向、70 米风向、10 米风向、海平面气压、云量、潜热通量、感热通量、短波辐射通量、长波辐射通量、地表水压、总降水、大尺度降水、对流降水、2 米温度、2 米相对湿度等数据。

数据指标介绍

 算法内容

import joblib
import pandas as pd
import numpy as np
from fbprophet import Prophet
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

数据分析，维度稳定性评估

df = pd.read_csv("JSFD003_base_1.csv", index_col="Unnamed: 0")
df["时间"] = pd.to_datetime(df['时间'])

def smooth_test(col):
    name = col.split("（")[0]
    smooth_df = df.loc[:, ['时间', col]]
    smooth_df = smooth_df.set_index("时间")
    y_ = smooth_df[col][::50].astype('float')
    # y_ = smooth_df['实际功率(MW)'][::].astype('float')

    # -------------一阶差分数据---------------------------
    y_diff = y_.diff(1).dropna()

    # -----------------绘制图形---------------------------
    '''
    可视化数据即绘制时间序列的折线图，看曲线是否围绕某一数值上下波动（判断均值是否稳定），
    看曲线上下波动幅度变化大不大（判断方差是否稳定），看曲线不同时间段波动的频率[~紧凑程度]
    变化大不大（判断协方差是否稳定），以此来判断时间序列是否是平稳的。
    '''
    plt.figure(figsize=(12, 6))
    plt.plot(y_)
    plt.title(rf"{name}")
    plt.show()
    # plt.savefig(rf"专利/{name}折线图.png")

    plt.figure(figsize=(12, 6))
    plt.plot(y_diff)
    plt.title(rf"{name}_一阶差分")
    plt.show()
    # plt.savefig(rf"专利/{name}一阶差分.png")

    '''
    可视化统计特征，是指绘制时间序列的自相关图和偏自相关图，根据自相关图的表现来判断序列是否平稳。
    自相关也叫序列相关，是一个信号与自身不同时间点的相关度，或者说与自身的延迟拷贝--或滞后--的相关性，是延迟的函数。不同滞后期得到的自相关系数，叫自相关图。
    （这里有一个默认假设，即序列是平稳的，平稳序列的自相关性只和时间间隔k有关，不随时间t的变化而变化，因而可以称自相关函数是延迟（k）的函数）
    平稳序列通常具有短期相关性，对于平稳的时间序列，自相关系数往往会迅速退化到零（滞后期越短相关性越高，滞后期为0时，相关性为1）；
    而对于非平稳的数据，退化会发生得更慢，或存在先减后增或者周期性的波动等变动。
    '''
    import statsmodels.api as sm
    from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
    # 例子
    # X = [2,3,4,3,8,7]
    # print(sm.tsa.stattools.acf(X, nlags=1, adjusted=True))
    fig, ax = plt.subplots(2, 2)

    plot_acf(y_, ax=ax[0][0])
    ax[0][0].set_title(rf"ACF:{name}")
    plot_pacf(y_, ax=ax[0][1])
    ax[0][1].set_title(rf'PACF:{name}')

    plot_acf(y_diff, ax=ax[1][0])
    ax[1][0].set_title(rf'ACF:{name}_diff')
    plot_pacf(y_diff, ax=ax[1][1])
    ax[1][1].set_title(rf'PACF:{name}_diff')
    plt.show()
    # plt.savefig(rf"专利/{name}自相关图和偏自相关图.png")

平稳性可视化效果:

 

 

等，对每一列做个平稳性分析，做选取较为平稳有使用价值的数据字段。 再本项目中

最终选择特征量为：

['实际功率(MW)', '10米高度处风速（m/s）',  '30米高度处风速（m/s）', '50米高度处风速（m/s）', '50米高度处风向（°）', '70米高度处风速（m/s）', '气温（°C）','气压（hpa）', '相对湿度（%）',]

时序预测模型

 时序预测法是根据历史统计数据的时间序列，对未来的变化趋势进行预测分析。一般来说，时间序列由四种变化成分组成，如长期趋势变化、季节性变化、周期性变化和随机波动。 一些简单的预测模型可用来预测上述三种趋势变化，如指数平滑模型、移动平均模型等。常用的时序性模型有arima，prophet，lstm，我们这里先使用prophet进行时序预测。

对比图示例。 

时序模型重新构建数据集

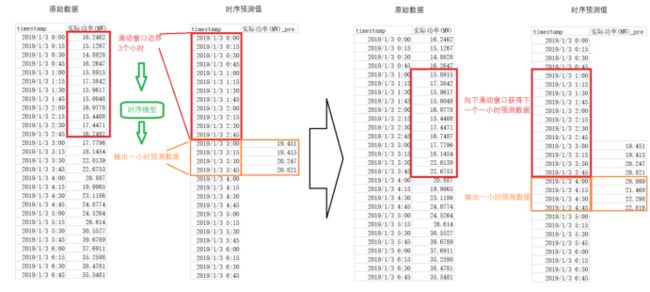
本项目中使用时序模型，滑动窗口的方式构建各个参数字段时序预测值构成的数据集。

通过滑动窗口获取预测数据组成的训练数集的步骤。

单列滑动窗口形成数据（以功率为例）

以滑动窗口为3小时，预测一小时举例子：

 

上图表示，黄框中的一小时数据（4条）是由时序模型通过钱三小时数据（12条）预测形成。

滑动窗口中的3小时数据，每间隔一小时的向下滑动（4条间隔），可以由新的窗口中的数据产生新的一小时的预测数据。

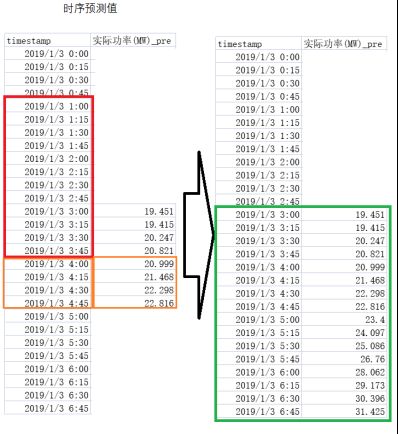
依次向下移动窗口，补全下面数据我们就得到了绿框中的数据，这些居于时序模型的预测数据是处了第一个滑动窗口对应的时间段没有数据，其他的时间段都有相应的”y_pre”数据。

接下来我们将真实值和滑动窗口预测值画折线图做对比：

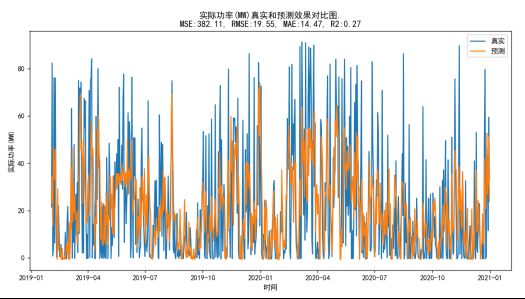
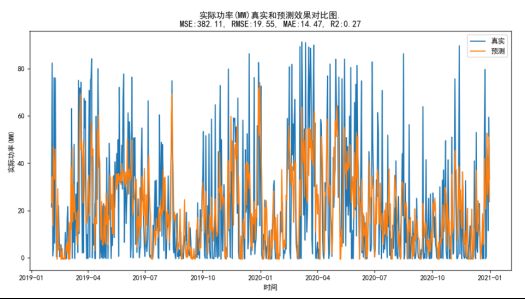 我们可以发现，真实值和预测值值波动趋势相似的，但是预测值的振幅要比真实值轻微了许多。这里预测值比真实值表现出了更好的数据平稳性。也许功率的数据这一变化表现的不是很明显，我们在看下对特征中风速的处理之后的对比，看起来会更清晰些。

 

整合其他列数据：

对功率列整理完成后，在对另外8列特征依次做相同的处理，并且将第一次滑动窗口所在的时刻的行去掉（因为没有预测数据），得到这样的数据：

 

 我们使用这样的经过滑动窗口时序预测之后的数据，训练我们的有监督模型（XGB）模型。会比原始数据表现出更好的拟合性。这些数据就是通过滑动窗口获取预测数据组成的训练数集。

def phet(phet_df, col, stat_time):
    # phet_df = phet_df.loc[:, ['时间', str]]
    phet_df = phet_df.rename(columns={'时间': 'ds', col: 'y'})
    print(phet_df)
    # 判断fit数据集是否有数
    if len(phet_df) > 2:
        # 拟合模型
        m = Prophet()
        m.fit(phet_df)
        # 构建待预测日期数据框，periods = 1 代表除历史数据的日期外再往后推 15分钟，即未来15分钟
        future = m.make_future_dataframe(periods=stat_time, freq='15min')
        # 预测数据集
        forecast = m.predict(future)
        # forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail()
        forecast['yhat_upper'] = forecast['yhat_upper'] * 1.01
        forecast['yhat_lower'] = forecast['yhat_lower'] * 0.99
        # print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']])
        # trend = forecast['yhat'].tolist()

        # 展示预测结果
        # m.plot(forecast)
        # m.plot(forecast).savefig('qushi.png')
        # 预测的成分分析绘图，展示预测中的趋势、周效应和年度效应
        # m.plot_components(forecast)
        # # m.plot_components(forecast).savefig('three_img.png')
        # plt.show()

        # 创建预测值df
        # res_df = pd.DataFrame()
        # res_df['时间'] = forecast['ds'][-stat_time:]
        # res_df[col] = round(forecast['yhat'][-stat_time:])
        # # #增加预测上限和下限制
        # res_df["yhat_upper"] = round(forecast['yhat_upper'][-stat_time:])
        # res_df["yhat_lower"] = round(forecast['yhat_lower'][-stat_time:])
        # # # # 保留小数
        # # res_df[col] = round(res_df[col], 2)
        # print(res_df)

        thres_df = round(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']][-stat_time:], 3)
        thres_df[col] = phet_df["y"][-stat_time:].tolist()
        thres_df.columns = ['时间', col + '_pre', col + '_l', col + '_u', col]
        print(thres_df)
        # print(thres_df)
        # print(thres_df.shape)
        return thres_df
    else:
        print('数据量不够')
        return None


# 时序数据处理
def data_loder():
    # 选出要分析的列
    DFdata = df.loc[:, ['时间', '实际功率(MW)', '10米高度处风速（m/s）', '10米高度处风向（°）', '30米高度处风速（m/s）',
                        '30米高度处风向（°）', '50米高度处风速（m/s）', '50米高度处风向（°）', '70米高度处风速（m/s）',
                        '70米高度处风向（°）', '风机轮毂高度处风速（m/s）', '风机轮毂高度处风向（°）', '气温（°C）',
                        '气压（hpa）', '相对湿度（%）', ]]
    # 获取开始预测时间
    '''
    表示从'2021/7/1 19:00:00'开始，每三分钟为一个单位，到'2021/7/14 23:59:30'为止
    输出样例 ['2021-07-14 23:42:00', '2021-07-14 23:45:00','2021-07-14 23:48:00','2021-07-14 23:51:00','2021-07-14 23:54:00', '2021-07-14 23:57:00']
    times=pd.date_range(start='2021/7/1 19:00:00',end='2021/7/14 23:59:30',freq='3min')
    '''
    times = pd.date_range(start='2019/2/2 23:45:00', end='2020/12/31 23:45:00', freq='1D')
    columns = ['实际功率(MW)', '10米高度处风速（m/s）', '30米高度处风速（m/s）', '50米高度处风速（m/s）', '70米高度处风向（°）',
               '70米高度处风速（m/s）', '气温（°C）', '气压（hpa）', '相对湿度（%）']
    # print(times)

    # 预测值df
    pre_df = pd.DataFrame()
    # print(times[0]-datetime.timedelta(hours=1))
    for t in times:
        pre_ = pd.DataFrame()
        for col in columns:
            # 选出时间区间的df
            new_df = DFdata[DFdata['时间'] < t][-(96 * 30 + 96):-96]
            # print(new_df)
            stat_time = 96
            pre = phet(new_df, col, stat_time)

            # pre[col] = new_df[col][-1:].tolist()
            # break
            # 合并预测值、阈值
            if col == columns[0]:
                pre_ = pre
                continue
            pre_ = pd.merge(pre_, pre, on='时间', how='inner')
            break
        pre_df = pre_df.append(pre_)
        # yield pre_df
        print('=============================', pre_df.shape, '==========================')
        break
    # pre_df.to_csv(f'综合指标时序预测结果.csv')

 画图的代码：

def pic_com(col):
    df_com = pd.read_csv("综合指标时序预测结果_修正后.csv")
    df_com["时间"] = pd.to_datetime(df_com['时间'])
    # print(df_com.columns.tolist())
    df_com_tar = df_com.loc[:, ["时间", col, rf"{col}_pre"]]

    # ================计算差距mse,mae,rmse,r2=============
    df_test = df_com_tar.sample(frac=0.2, replace=False, axis=0, random_state=1)
    # print(len(df_com_tar))
    # print(len(df_test))
    # print(df_test.info())

    y_ture = df_test[col]
    y_pre = df_test[rf"{col}_pre"]
    # print(len(y_ture))
    from sklearn.metrics import mean_squared_error  # MSE
    from sklearn.metrics import mean_absolute_error  # MAE
    from sklearn.metrics import r2_score

    MSE = mean_squared_error(y_ture, y_pre)
    RMSE = np.sqrt(MSE)
    MAE = mean_absolute_error(y_ture, y_pre)
    R2 = r2_score(y_ture, y_pre)
    # print(MSE,RMSE,MAE,R2)

    # =====================画折现对比图===================
    Xtime_list = df_com_tar["时间"].tolist()[::96]
    Yture_list = df_com_tar[rf"{col}"].tolist()[::96]
    Ypre_list = df_com_tar[rf"{col}_pre"].tolist()[::96]

    plt.figure(figsize=(12, 6))
    plt.plot(Xtime_list, Yture_list)
    plt.plot(Xtime_list, Ypre_list)
    plt.title(col + "真实和预测效果对比图.\nMSE:%.2f, RMSE:%.2f, MAE:%.2f, R2:%.2f" % (MSE, RMSE, MAE, R2))
    plt.xlabel('时间')  # 为x轴命名为“x”
    plt.ylabel(rf"{col}")  # 为y轴命名为“y”
    plt.legend(['真实', '预测'])  # 打出图例
    plt.show()

 滑动窗口生成的新的数据还需要进一步处理修正，比如风速实际不会小于0 ，但是在滑动窗口预测时则有可能小于0.,这些不是正常范围的值需要再处理一下。

def correction():
    '''
    预测表修正列：
    实际功率(MW)_pre ：值小于0.5的 = 0.5
    10米高度处风速（m/s）：值小于0的 = 0
    30米高度处风速（m/s）：值小于0的 = 0
    50米高度处风速（m/s）：值小于0的 = 0
    70米高度处风速（m/s）：值小于0的 = 0
    相对湿度（%）：值小于0的 = 0
    '''
    df_before = pd.read_csv("综合指标时序预测结果.csv")
    df_before.drop('Unnamed: 0', axis=1, inplace=True)

    df_before['实际功率(MW)_pre'] = df_before['实际功率(MW)_pre'].apply(lambda x: -0.5 if x < -0.5 else x)
    df_before['实际功率(MW)_l'] = df_before['实际功率(MW)_l'].apply(lambda x: -0.5 if x < - 0.5 else x)
    df_before['实际功率(MW)_u'] = df_before['实际功率(MW)_u'].apply(lambda x: -0.5 if x < -0.5 else x)

    df_before['10米高度处风速（m/s）_pre'] = df_before['10米高度处风速（m/s）_pre'].apply(lambda x: 0 if x < 0 else x)
    df_before['10米高度处风速（m/s）_l'] = df_before['10米高度处风速（m/s）_l'].apply(lambda x: 0 if x < 0 else x)
    df_before['10米高度处风速（m/s）_u'] = df_before['10米高度处风速（m/s）_u'].apply(lambda x: 0 if x < 0 else x)

    df_before['30米高度处风速（m/s）_pre'] = df_before['30米高度处风速（m/s）_pre'].apply(lambda x: 0 if x < 0 else x)
    df_before['30米高度处风速（m/s）_l'] = df_before['30米高度处风速（m/s）_l'].apply(lambda x: 0 if x < 0 else x)
    df_before['30米高度处风速（m/s）_u'] = df_before['30米高度处风速（m/s）_u'].apply(lambda x: 0 if x < 0 else x)

    df_before['70米高度处风速（m/s）_pre'] = df_before['70米高度处风速（m/s）_pre'].apply(lambda x: 0 if x < 0 else x)
    df_before['70米高度处风速（m/s）_l'] = df_before['70米高度处风速（m/s）_l'].apply(lambda x: 0 if x < 0 else x)
    df_before['70米高度处风速（m/s）_u'] = df_before['70米高度处风速（m/s）_u'].apply(lambda x: 0 if x < 0 else x)

    df_before['相对湿度（%）_pre'] = df_before['相对湿度（%）_pre'].apply(lambda x: 0 if x < 0 else x)
    df_before['相对湿度（%）_l'] = df_before['相对湿度（%）_l'].apply(lambda x: 0 if x < 0 else x)
    df_before['相对湿度（%）_u'] = df_before['相对湿度（%）_u'].apply(lambda x: 0 if x < 0 else x)

    # df_res = df_before.loc[:,['实际功率(MW)_pre', '10米高度处风速（m/s）_pre', '30米高度处风速（m/s）_pre', '70米高度处风速（m/s）_pre', '相对湿度（%）_pre']]
    # print(df_before.describe())
    df_before.to_csv("综合指标时序预测结果_修正后.csv")

Xgb+时序模型预测数据集

检测设备上所记录的实时气象数据，存在稳定性较差的特性。这样的数据特性训练有监督的学习算法，容易使得简单模型抓不住数据中的规律欠拟合，而复杂模型容易拟合规律细节而过拟合，反映在杨验证集中的评分就不太理性。

我们发现使用滑动窗口时序预测应用于以往的数据中，可以形成又预测数据组成的训练数集和。这些预测数据对比真实数据展现了稳定性上的提上。所以在有监督训练XGB模型阶段，使用特征的预测数据集，有利于提高模型的性能。最总在验证集上提升表现。

结果输出：

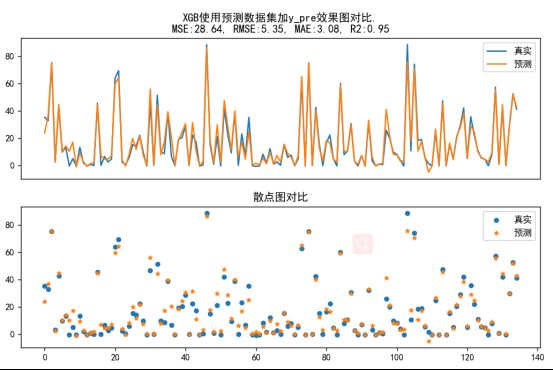
Xgb使用预测数据做数据集训练，在验证集上的效果：

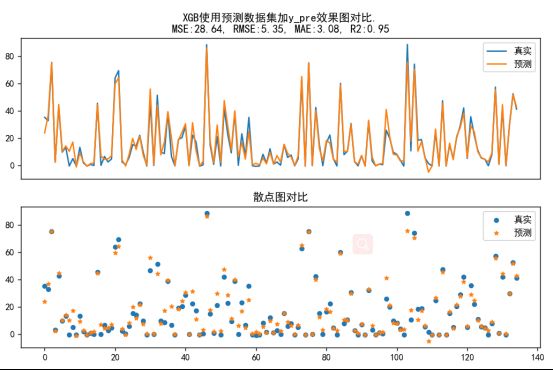
 Xgb使用预测数据增加加y_pre（功率的滑动窗口预测值）做数据集训练，在验证集上的效果：

def Xgb():
    # 数据加载
    df_corr = pd.read_csv("综合指标时序预测结果_修正后.csv")
    df_corr["时间"] = pd.to_datetime(df_corr["时间"])

    DFdata = df_corr.loc[:, ['时间', '实际功率(MW)', '10米高度处风速（m/s）_pre', '30米高度处风速（m/s）_pre',
                             '50米高度处风速（m/s）_pre', '70米高度处风向（°）_pre', '70米高度处风速（m/s）_pre',
                             '气温（°C）_pre', '气压（hpa）_pre', '相对湿度（%）_pre']]
    feature_name = ['10米高度处风速（m/s）_pre', '30米高度处风速（m/s）_pre',
                    '50米高度处风速（m/s）_pre', '70米高度处风向（°）_pre', '70米高度处风速（m/s）_pre',
                    '气温（°C）_pre', '气压（hpa）_pre', '相对湿度（%）_pre']

    target_name = "实际功率(MW)"

    X = DFdata[feature_name]
    y = DFdata[target_name]

    xbg_model = XGBRegressor(
        # 一、通用参数
        booster='gbtree',  # 设置基础模型是谁？可以树 可以线性模型
        # 二、booster参数设置，比如树相关的深度、叶子节点
        n_estimators=150,
        max_depth=17,
        random_state=0,
        # 三、任务参数， 主要设置目标函数
        eval_metric='mlogloss',
        use_label_encoder=False,
    )

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)

    '''
    from sklearn.model_selection import GridSearchCV  # cv网格认证最好的参数
    param_grid = {"n_estimators": range(50, 151, 50), "max_depth": range(10, 31, 10)}
    grid = GridSearchCV(xbg_model, param_grid=param_grid, cv=2)
    grid.fit(X_train, y_train)
    print(grid.best_params_)
    '''
    # print(X_train.shape, y_train.shape)
    xbg_model.fit(X_train, y_train)

    y_pred = xbg_model.predict(X_test)
    from sklearn.metrics import mean_squared_error  # MSE
    from sklearn.metrics import mean_absolute_error  # MAE

    # print("均方误差", mean_squared_error(y_test, y_pred))
    # print("均方根误差RMSE", np.sqrt(mean_squared_error(y_test, y_pred)))
    # print("平均绝对误差MAE", mean_absolute_error(y_test, y_pred))
    # print("R2", xbg_model.score(X_test, y_test))

    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(mean_squared_error(y_test, y_pred))
    MAE = mean_absolute_error(y_test, y_pred)
    R2 = xbg_model.score(X_test, y_test)

    # 可视化
    # 以样本编号为x轴；真实结果作为y轴
    # y_pred y_test下采样，采样间距100(为了画图方便)
    x_data = np.arange(len(X_test[::100]))
    y_pred_1 = y_pred[::100]
    y_test_1 = y_test[::100]

    fig = plt.figure(figsize=(10, 6))

    fig.add_subplot(2, 1, 1)  # 1行2列的第一个子图， 激活第一个子图
    plt.plot(x_data, y_test_1)  # 真实结果
    plt.plot(x_data, y_pred_1)  # 预测结果
    plt.legend(["真实", "预测"])
    plt.title(f"XGB使用预测数据集效果图对比.\nMSE:%.2f, RMSE:%.2f, MAE:%.2f, R2:%.2f" % (MSE, RMSE, MAE, R2))
    plt.xticks([])

    fig.add_subplot(2, 1, 2)  # 2行1列的第一个子图， 激活第一个子图
    plt.scatter(x_data, y_test_1,
                marker='o',  # 点的样式，圆圈
                s=20,  # 点的大小
                )
    plt.scatter(x_data, y_pred_1,
                marker='*',  # 点的样式，圆圈
                s=20,  # 点的大小
                )
    plt.title("散点图对比")
    plt.legend(["真实", "预测"])
    # plt.savefig(rf"images_metrics/{fd_name}厂模型指标.jpg")
    plt.show()
    # xbg_model.fit(X, y)
    # joblib.dump(xbg_model, 'xgb_y_pre.model')

结论点：

1， 该方法可以解决一个现实问题：有监督学习预测未来数据的能力。（在风电机传感器未采集到未来指标数据的情况下，依旧可以创造出输入数据使用有监督学习得到目标结果。）

 2，该方法在数据稳定性上，增进了数据的稳定性，从而提高了XGB(有监督学习模型)性能。正是这个原因，本来建立在预测数据（滑动窗口预测数据集）上的预测模型（XBG）在感官上应该性能下降才是，但是在是实验结果上性能上升的原因。对于不稳定维度数据，该方法有奇效。

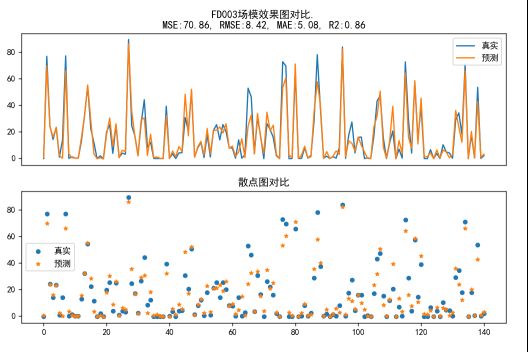
3，这个方法相比较而言性能分值都有所提高：

时序模型预测功率值：R2得分0.27

 

XBG根据已发生的指标数据预测功率值：R2得分0.86

 

XGB(有监督学习)和多维时序模型结合的方式分值最高，且不受未来数据的束缚。