模式识别系列（五）对偶支撑向量机和核向量机

1.对偶支撑向量机

1.1对偶问题

1.1.1线性规划对偶问题

  在提出对偶支撑向量机之前，先得有对偶的概念。对偶就是对同一个问题，从不同的角度描述。举一个简单的例子，当周长一定，面积最大的矩形是正方形，而当面积一定，周长最小的矩形是正方形，这就是两个对偶的表述。再举一个例子，一个工厂可以选择出租设备或者生产产品，如果站在他的角度，那自然生产的利益要最大化，而站在租用设备的人的角度，他所付出的钱希望是最少的，从两边看对偶问题就是把一个最大值问题变成了最小值问题，因此线性规划中的对偶问题有如下标准型：
$$\begin{array}{rl}& \begin{array}{cccc}\min w=yb& & \max z& =cx\\ yA\ge c& & Ax& \le b\\ y\ge 0& & x\ge 0& \end{array}\end{array}$$
这两个问题就互为对偶问题。对偶问题满足弱对偶性，即上式中的前者大于等于后者，就好像高个中挑个矮的，要比矮个中挑个高的来的高。

1.1.2拉格朗日对偶问题

  拉格朗日对偶问题就是对拉格朗日函数进行对偶所形成的问题。首先，我们有一个目标函数的标准型：
$$\begin{array}{lc}\min & f(x)\\ \text{ s.t. }& c_i(x)\le 0,i=1,2,\cdots ,k\\ & h_j(x)=0,j=1,2,\cdots ,l\end{array}$$
那么我们就可以通过拉格朗日函数的方式将约束放进函数里
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)，a_i\ge 0$$
随后我们令拉格朗日函数最大化
$${\theta }_P(x)=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
假如有违反约束的值出现，比如$c_i(x)>0$ 或者$h_j(x)\ne 0$，由于$\alpha$和$\beta$是我们可以手动选择的，那么我们就可以选择一个趋向$+\infty$的$\alpha$，让上面的函数最大值是无穷，也就是没有最大值。而相反，当自变量$x$满足约束条件，${\theta }_p(x)$取极大值时，$\alpha$只能是0，而$\beta$对于函数值没有影响，最后的结果就是
$${\theta }_P(x)=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\left[f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)\right]=f(x)$$
由此一来，原问题就变成了
$$p^{\ast }=\underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
再从另外一个角度出发，由于$\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )=f(x)$那么自然而然$f(x)\ge L(x,\alpha ,\beta )$是成立的，因而
$$\min f(x)\ge \underset{x}{\min }L(X,\alpha ,\beta )=d$$
显然：
$$\underset{x}{\min }L(x,\alpha ,\beta )\le L(x,\alpha ,\beta )\le \underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
那么现在就可以考虑这样一个问题，令$d^{\ast }=\max d$,即：
$$d^{\ast }=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$
从形式上$p^{\ast }$和$d^{\ast }$正好形成对偶,而且满足弱对偶性，即$d^{\ast }\le q^{\ast }$。究其原因，就在于$d$和$q$的变量是不一致的，$d$的变量是$\alpha$和$\beta$，给出了原函数的一个下界，而$q$的变量是$x$，$q^{\ast }$求的是原函数的最小值，而我们知道，一个函数的下界是小于函数最小值的，但我们可以通过求下确界，也就是求$d^{\ast }$,来逼近函数的最小值，这就是拉格朗日对偶法的基本思想。如果原函数是一个凸函数，那么$d^{\ast }$=$p^{\ast }$是成立的，这就是强对偶性。
  本篇的内容是对偶SVM，我们花了这么多篇幅来解释拉格朗日对偶，原因就在于此：当原问题$p^{\ast }$不那么好求的时候，我们可以用对偶的$d^{\ast }$来求解，达到一个近似逼近的效果。

1.2概念提出

  首先我们来温习一下标准SVM的目标函数：
$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2\\ & \\ \text{ s.t. }& y_i\left(w^T\cdot x_i+b\right)\ge 1,i=1,2,\dots ,N\end{array}$$
那么求解的变量就有$d+1$个维度，在实际中，如果我们要拟合非线性的多项式，那么势必要对原始输入变量进行升维，比如将$(x1,x2)$变成$(x1,x2,x1x2,x{1}^2,x{2}^2)$，诸如此类。这还仅仅是二元二次，还有更高次的变换，这样很可能特征向量的维度就很高了，优化的困难无疑变大了。因此我们可以用上节提到的拉格朗日乘子法，改写目标函数：
$$\underset{w,b}{\min }\underset{{\alpha }_i\ge 0}{\max }\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^N{\alpha }_i(y_i{w}^T\cdot x_i+y_{i}b)+\sum _{i=1}^N{\alpha }_i$$
通过对偶拉格朗日，将目标函数改为：
$$\underset{{\alpha }_i\ge 0}{\max }\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^N{\alpha }_i(y_i{w}^T\cdot x_i+y_{i}b)+\sum _{i=1}^N{\alpha }_i$$
通过下界去逼近，此时这个目标函数就变成了了${\alpha }_i$的函数，而${\alpha }_i$就和维度一点关系都没有了，只和样本数量有关，这就转移了优化的难点。

1.3公式推导

  在上节我们给出了对偶向量机的拉格朗日对偶函数，那么这个函数怎么优化呢？首先我们看里面，是一个无约束的函数吧，那么是不是可以求极值点呢？，分别对$w$和$b$求偏导，得到以下结果：
$$\begin{array}{rl}& \frac{\partial L}{\partial b}=-\sum _{i=1}^N{\alpha }_i{y}_i\\ & \frac{\partial L}{\partial w}=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\end{array}$$
上面两个偏导都只有一个极值点，那么我们就可以令${\sum }_{i=1}^N{\alpha }_i{y}_i=0$,$w={\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i$,此时目标函数就变成了${\alpha }_i$的单变量函数，即：
$$\underset{{\alpha }_i\ge 0；{\sum }_{i=1}^N{\alpha }_i{y}_i=0；w={\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i}{\max }\frac{1}{2}\Vert \sum _{i=1}^N{\alpha }_i{y}_i{x}_i{\Vert }^2+\sum _{i=1}^N{\alpha }_i$$
之所以可以这么做，是因为在进行对偶后自变量发生了改变,整个是$\alpha$的函数，内外就可以分离了。
提出一个负号，问题就变成了：
$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^N{\alpha }_i\\ \text{ s.t }& \sum _{i=1}^N{y}_i{\alpha }_i=0;\\ & {\alpha }_i\ge 0,\text{ for }i=1,2,\dots ,N\end{array}$$

1.4对偶支撑向量机求解

对于上面一节的问题，我们可以对比二次规划的标准型：
$$\begin{array}{rl}& \min q(z)=\frac{1}{2}{z}^{T}Gz+z^{T}c\\ \text{s.t.}& a_i^{T}x\ge b_i,i\in \tau \end{array}$$
和上一篇一样，我们只需要令
$$z=\alpha ;G_{i,j}=y_i{y}_j{x}_i^T{x}_j;c=-1;{\mathbf{a}}_i^T=y_i;b_i=0$$
就能转化成二次规划问题了。

  求解出了${\alpha }_i$,就可以根据$w={\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i$得出向量$w$,根据$a_{i}n(1-y_i(w^T{x}_i+b))=0$,求得$b$。$a_n>0$的这些向量就是所谓的支撑向量，处在边界上的这些向量。

2.核向量机

2.1问题提出

  核向量机是基于对偶向量机的。在对偶向量机中，虽然优化的维度不随特征的维度增加而增加，但是并不代表向量的特征维度不会影响计算复杂度，可以看到，式中有一项$x_i^{T}xj$,复杂度很高的。因此就提出了核向量机的概念，即——升维后的内积是不是可以由升维前的内积直接得到。

2.2核函数和核矩阵

  假设$\varphi (x)$是升维的函数，那么核函数用数学语言描述就是：
$$K<x,z>=<\varphi (x),\varphi (z)>$$
K表示对的内积进行变换。举一个具体的例子，假如说$\varphi (x)=(x^2,\sqrt{2}xy,y^2)$, $K<x_1,x_2>=(x_1^T{x}_2{)}^2$,那么显然：
$$\begin{array}{rl}\varphi (x_1{)}^T\varphi (x_2)=& <(x_1^2,\sqrt{2}{x}_1{y}_1,y_1^2),(x_2^2,\sqrt{2}{x}_2{y}_2,y_2^2)>\\ =& x_1^2{x}_2^2+2x_1{y}_1{x}_2{y}_2+y_1^2{y}_2^2\\ =& (x_1{y}_1+x_2{y}_2{)}^2\\ =& (x_1^T{x}_2{)}^2\end{array}$$
核函数的方式，等于说仅仅计算了升维前的内积，可以大大减少计算量。常用的多项式核函数有如下的形式：
$$K(x_i,x_j)=(\alpha +\beta x_i^T{x}_j{)}^n$$
另外高斯核函数也是常用的核函数，形式如下：
$$K(x_i,x_j)=e^{-\frac{\Vert x_i-x_j{\Vert }^2}{2{\sigma }^2}}$$
高斯核又称无穷维度的核函数，原理很简单，用微积分里的麦克劳林展开公式展开这个指数函数就行了，会发现是一个无穷维度多项式求和的形式。在sklearn库里常用的RBF核就是高斯核，参数gamma就正比于$\frac{1}{{\sigma }^2}$,我个人的理解$\sigma$类似于一个样本的影响范围，当它很大，高斯函数就比较平缓，一个正样本会增加附近样本的正向概率，当它很小，一个正样本很可能只能保证自己的正向概率，类比起来就像是连绵的群山和山洞里的钟乳石这样。
  当然，我们自然可以自己设计这么一个核函数,要求就是满足核矩阵板正定，也就是
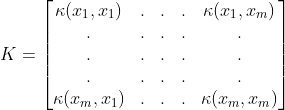半正定$x^{T}Kx\ge 0$,这方面没有学习，有兴趣可以自己搜索相关内容

2.3核向量机

  有了上面的基础，核向量机也就自然而然可以写出来了，形式为：
$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K<x_i,x_j>-\sum _{i=1}^N{\alpha }_i\\ \text{ s.t }& \sum _{i=1}^N{y}_i{\alpha }_i=0;\\ & {\alpha }_i\ge 0,\text{ for }i=1,2,\dots ,N\end{array}$$
到这里，支撑向量机部分施工完毕。