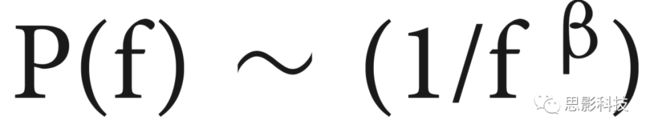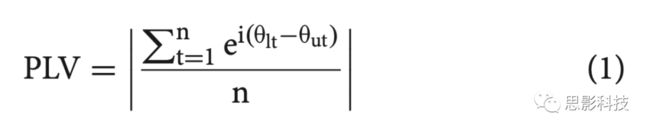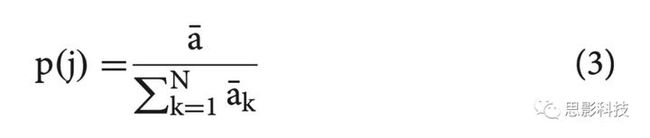神经元振荡中相位幅值耦合的量化:锁相值、平均向量长度、调制指数和广义线性模型交叉频率耦合
相位振幅耦合是研究脑电和脑磁图中认知过程的一个很有前途的方法。由于概念新颖,文献中采用了多种方法来计算相幅耦合。本文利用模拟数据对锁相值(PLV)、平均向量长度(MVL)和调制指数(MI)这三种最常用的相幅耦合测量方法和广义线性模型交叉频率耦合(GLM-CFC)方法的性能进行了比较。我们结合了以前的文章的优点,并使用一个真实的数据模拟检查调节变量,并提供推论的统计数据,以比较所有四个指标的相位-幅度耦合。分析表明,当存在单相(monophasic)耦合时,这四个指标都能成功地区分耦合强度和耦合宽度。而MVL对耦合强度和宽度的调制最敏感,只有MI和GLM-CFC可以检测到双相(biphasic)耦合。在接近Nyquist频率时,4个指标的耦合值都受数据长度、信噪比和采样率等调节因子的影响。MI对这些调节因子的混杂影响最鲁棒。基于我们的分析,我们推荐MI用于耦合形式未知的噪声和短数据。对于有着单相耦合和高信噪比的高质量和长的数据,推荐使用MVL。理想情况下,对一个数据集同时报告两个指标。本文发表在Frontiers in Neuroscience杂志。
关键词:相位幅值交叉频率耦合;锁相值;平均向量长度;调制指数;GLM-CFC;
1.引言
相位幅值耦合是研究认知过程的一种很有前途的方法。相位幅值耦合的计算方法目前还没有统一的规定,但文献中所用的相位幅值计算方法存在很大的异质性。从理论角度来看,这些大部分都是合理的。本文利用模拟脑电图数据,对三种常用的相幅耦合测量方法的性能进行了全面的比较,为选择这些方法提供了经验证据。测量方法是Mormann等人使用的锁相值(PLV), , Canolty等人使用的平均向量长度(MVL),以及Tort等人使用的调制指数(MI)。此外,还检查了GLM-CFC。
从以前的观点来看,首先检测到的振幅调制是特定频段的振幅波动,在这些信号成分在快速傅里叶变换(FFT)中变得明显。因为FFT方法只能揭示高频振荡在低频振荡上的振幅(一个信号的特征),这些幅值调制不应该被误解为解释较低频率的瞬时相位和较高频率的振幅包络之间的真正的时间耦合(两个信号之间的关联和相位-幅值耦合的定义)。这种方法既不能提取低频本身,也不能提取其瞬时相位。
如今一些使用广泛的相位幅值耦合,如PLV(也叫同步指数SI),MVL,MI,包络信号相关 (envelope-to-signal correlation,ESC),广义线性模型方法(GLM),相位均分并结合ANOVA(BA),和加权锁相因子(wPLF)。最近有方法使用互信息来计算相幅耦合。互信息的计算对数据量和噪声很敏感,但在处理非线性关系时比较有利。所有这些测量都使用带通滤波信号的瞬时相位和振幅来计算耦合强度值。然而,不同的测量方法在概念和数学原理上有很大的不同。
在以往的研究中,我们将几种相位幅值耦合方法与模拟和实际数据进行了比较。Tort等人进行了迄今为止最广泛的比较,包括上面列出的大部分方法,并评估了它们对噪声的耐受性、幅值独立性、对多模态的敏感性和对调制宽度的敏感性方面的性能。他们得到的结果为,MI在所有方面都得到了很好的评价,而PLV在所有方面都得到了很差的评价。MVL在某些方面有良好的评价(例如,对噪声的耐受性),但存在其他方面的弱点(例如,幅值依赖性)。
Penny等人介绍了GLM方法,并在噪声水平、耦合相位、数据长度、采样率、信号非平稳性和多模态等方面与PLV、MVL和包络信号相关性进行了比较。他们发现,这些方法可以在不同程度上区分有耦合和没有耦合的模拟数据,范围从低于机会随机水平到完全区分。在较差的条件下(高噪声、低采样率等),这些方法的性能各不相同,但是,所有方法在较好的条件下(较长数据、较低噪声等)表现同样良好。
Kramer和Eden提出了一种新的GLM方法(GLM-CFC),证明是有效的,并且表现得和MI一样好。这种方法的优点是它可以解释调制引起的振幅强度的百分比变化,这种方法的置信区间易于计算和测量,而且可以检测双相耦合。该方法的缺点是计算时间特别长,因为需要生成GLM的设计矩阵并对其进行拟合。
Onslow等人比较了三种相位振幅耦合测量(MVL,包络-信号相关,交叉频率相干),他们发现“没有一种测量总是优于其他的”。他们得出的结论是,每种方法似乎都特别适合于特定的数据条件。例如,MVL适用于有噪声的数据、探索性分析(分析一个宽频谱)以及提供频段的幅值功率较低的情况。
Samiee和Baillet对PLV、MVL和MI进行了统计比较,特别关注了数据长度效应和在宽频率范围内探索性分析中找到贡献耦合频率的准确性。在这里,所有三种测量方法在精确寻找耦合频率方面表现得同样好。然而,他们的结果表明,在上述探索性分析中,MVL对耦合强度的估计最正确,而就检测正确的耦合频率而言,MI对噪声最鲁棒。作者表明,当使用复杂的方法检测数据中的相位和振幅的实际耦合频率时,MVL的性能可以显著提高,这种方法允许对非常短的数据段估计耦合强度。
上述引用的结论并没有指出计算相幅耦合的唯一的最佳方法。它们更确切地表明,大多数(但不是全部)使用的衡量标准表现良好,受到各种混杂因素的同等影响。尽管有多种测量方法可用,但79%的研究使用适合于相位振幅耦合的PLV、MVL或MI。这三种方法确实是最常用的。为什么会这样呢?PLV是一个长期使用的方法,相位-相位耦合测量很容易适应于相位-幅度测量的目的。MVL的主要应用可能是由于其数学上的直接性。MI在概念上是直观的。
大多数研究都使用了非常简单的数据模拟方法。通常,正弦振荡是在较低的提供相位的频率和较高的提供振幅的频率构造的。相位-幅度耦合是通过将两个信号相乘来实现的,然后从所构造的信号中提取振幅,并从较低频率的纯正弦振荡中提取相位。两个信号都加入白噪声。这种方法有两个缺点。这两个正弦信号都反映了一个简单的相幅耦合原型,但在真实的神经元数据中,纯正弦振荡不能被滤波;相反,包含不同数量的不同频率的频带被提取。其次,在模拟数据中加入白噪声,但是已知的是分形布朗噪声是大脑动力学固有的,而不是白噪声。
因为迄今为止,没有一个现有的综述同时满足真实模拟脑电图数据的要求,为测量方法的比较提供推断统计,研究相位振幅耦合的调节因子,并包括三个最广泛使用的测量方法(PLV,MVI和MI),本文对这些方法进行了新的比较。此外,GLM-CFC也包括在比较中。我们的目标是将之前所有结论的最佳方面结合起来。根据Kramer和Eden所描述的过程,对脑电图数据进行了较为逼真的模拟,研究了几种调节因子(多模态、数据长度、采样率、噪声水平、调制强度和调制宽度)的影响。根据所述方法,Onslow等人对相位振幅耦合测量的灵敏度和特异性进行了检查。对于所有这些比较,提供了推论统计。
2.材料与方法
脑电图数据仿真与相位幅值耦合的实现
脑电图数据的一个特征是其频谱与功率成正比
。也就是说,频率f越高,振幅P(f)越弱。β指数定义了振幅下降的强度。白噪声定义为β = 0,粉红噪声定义为β= 1,布朗(红)噪声β= 2。不同的研究表明,人类大脑活动的频谱与分形布朗(红色)噪声有关,其中2<β<3。因此,我们使用Zhivomirov提供的MATLAB代码产生布朗噪声,以模拟脑电图数据(图1A)。
对模拟数据的低频相位进行滤波,称为相位时间序列,带宽为2Hz。然后对相同的数据的高频振幅进行滤波,称为振幅时间序列,具有较宽的带宽。高频振幅时间序列的准确带宽应取决于相位时间序列的频率。由于对数据进行了滤波,总是包含调制频率的边界频带(即高频的中心频率±低频的上边界)。
采用了EEGLAB中的零相位汉明窗正弦有限脉冲响应(FIR)滤波器(pop_eegfiltnew)。该函数自动选择滤波器的最优阶数和过渡带宽,以精确选择滤波器带宽。低频为5 - 7Hz(用于theta-低gamma耦合)和8 - 10Hz(alpha-高gamma耦合)。高频设置为33-47Hz(用于theta-低gamma耦合)和50-70Hz(用于alpha-高gamma耦合)。
随后,利用MATLAB的信号处理工具箱,通过Hilbert变换提取相应的时间序列的相位和振幅。然后对连续的相位和幅值时间序列进行分割。这样做是为了引入数据的不连续性,这也存在于真实数据中。对连续数据进行滤波、希尔伯特变换,相位或幅度提取,以防止后期分段的数据出现滤波或其他伪迹。
然后对每个模拟数据集进行修改。对长度为42、105和180 s的数据集进行降采样。这个数据量足以模拟30个试次,长度分别为400、2500和5000 ms,再加上额外的30秒,以便在分割数据时引入数据的不连续。选择这些参数来反映事件相关脑电图数据的典型特征:(1)每一种计算相位振幅耦合的条件下,至少有30个试次;(2)试次长度在400 ~5000ms之间(3)试次之间的数据不连续性。采样率设置为1000Hz。此外,为了研究采样率的影响,模拟数据被重新采样到500Hz。噪声按因子0.9、1.0和1.1来模拟不同的信噪比。比例因子0.9、1.0和1.1,对应于噪声信号强度分别为90、100和110%(与数据信号强度相比)。实现了四种调制强度:无耦合时I = 0.0,增加耦合强度时I = 0.9, I = 1.0, I = 1.1 (I = 1.0表示2倍原始振幅强度)。这些值属于以前的研究范围。汉宁窗的长度在一个低频周期的22.5 ~ 27.5%之间,以调制不同的相位振幅调制的“宽度”。:这个宽度相当于一个周期的四分之一,因此涵盖了低频周期的峰值(或低谷)阶段。在此阶段,高频幅值增加。所有参数都实现了单、双相耦合。
图1 脑电图信号仿真及相位幅值耦合计算
(A)(从左到右)分别是首先产生布朗噪声原始信号,然后经过带通滤波,提取出慢的提供相位的低频(8-10hz,红线)和快的提供振幅的高频(50-70hz,深蓝线)。之后是非耦合和耦合的振幅图和相位图。
(B)4个指标的情况:
PLV:每条黑线表示两个信号在一个数据点的相位延迟。红色向量是所有黑色向量的平均值。上面的面板显示不一致、分散的相位滞后。分散的相位滞后导致相对较短的平均向量(红线)。左下面板显示了一个相对恒定的相位滞后,在0°左右。相对恒定的相位滞后导致相对长的平均向量。
MVL:每个黑点表示解析信号的一个数据点。在耦合的情况下,部分点(或向量)是特别长的(反映了强的振幅)。红色向量是所有黑色向量的平均值。它反映了耦合强度(短为无耦合-长为耦合)。
MI:所有可能的相位从-180°到180°以20°为间距分箱为18个。每个条形反映了提供相位的频率的特定相位对应的提供幅度的信号的平均振幅。此相位幅值图用香农熵进行量化。均匀分布的Shannon熵是最大的(上面板)。Kullback-Leibler距离度量给定的分布(例如下面板中的分布)与均匀分布(如上面板所示)的偏离程度。数据中相幅耦合越多,给定的相幅图偏离均匀分布越多,MI值越高。
GLM-CFC:散点图中的每个圆表示一个数据点。如果没有相位幅值耦合,振幅值在所有可能的相位值上是相当相似的。在这种情况下,水平线是数据最好的模型,而相位值没有预测能力。如果存在相位幅值耦合,在某些相位值时幅值特别高。在这种情况下,遵循振幅模式的曲线将最好地模拟数据。在相幅耦合的情况下,曲线(红线)与表示无耦合的水平线(黑线)不同。在没有相位振幅耦合的情况下,曲线与水平线表示没有耦合的模型几乎没有区别。
测量相位振幅耦合为了计算相幅耦合,首先对原始数据进行感兴趣频带的带通滤波。其次,将带通滤波后的带通信号转换为复数解析信号。最后,从解析信号中提取相位或振幅。所有这些步骤基本上可以在MATLAB中用四行代码实现:
Mormann等人对锁相值的应用对于PLV的计算,从低频滤波的解析信号中提取相位,从高频滤波的解析信号中提取幅值。然后振幅时间序列再次经过希尔伯特变换并从“第二次”解析信号中相位提取。通过这些步骤,可以得到每个数据点的两个时间序列的相位角。对于每个数据点,从相位时间序列的相位角中减去希尔伯特变换的振幅时间序列的相位角,得到相位角差。这些相位角差可以在极平面上以长度为1的向量表示,其中的角表示各自的相位角差(图1B,左外面板)。两个时间序列之间的恒定相位滞后表明相幅耦合。恒定的相位滞后导致极平面上的向量具有相似的方向。然后取所有向量的平均值:如果它们有恒定的相位滞后,它们指向相同的方向,导致一个相当长的平均向量。如果存在可变相位滞后,则向量分散在极面周围,导致较短的平均向量。平均向量的长度表示相幅耦合的量(耦合强度)。向量的方向表示两个时间序列之间的平均相位滞后,从相位滞后可以推断出首选耦合相位。PLV的计算公式如下:
其中n为数据点总数,t为一个数据点,θlt为数据点t的低频相位角,θut为希尔伯特变换后的高频振幅时间序列的相位角。该指标的逻辑是:如果存在相位幅值耦合,高频时间序列的幅值将在低频处振荡。在这种情况下,从该信号中提取瞬时相位信息将给低频的瞬时相位信息返回某些恒定的相位滞后。否则,提取的是低频的瞬时相位的不一致的相位滞后,说明没有相位幅值耦合。该方法的一个潜在缺点是,如果希尔伯特变换的振幅时间序列不以特定的频率振荡,将提取到无效的相位信息。在提取相位信息之前,可以通过对低频范围的希尔伯特变换的振副时间序列进行滤波来抵消这一缺点。需要注意的是,有意义的相位信息只能从窄带振荡中提取。希尔伯特变换的振幅时间序列不一定是这样的窄带振荡。
Canolty等的平均向量长度(MVI)Canolty等提出的相位幅值耦合指标是MVL,从低频滤波后的解析信号中提取相位,从高频滤波后的解析信号中提取幅值。MVL利用对应解析信号的每个复数(即每个数据点)的相位角和幅值,比较直接地估计耦合程度。解析时间序列的每个复值都是极平面上的一个向量。当所有向量的一部分的幅度M在一个特定的相位或在一个狭窄的相位范围内特别高时,就存在相位振幅耦合(图1B,左内面板)。对所有向量取平均值将创建一个具有特定相位和长度的平均向量(图1B中的红色向量)。这个向量的长度表示相幅耦合的量。方向代表振幅最强的平均相位。当不存在耦合时,所有向量相互抵消,平均向量将变短。那么它的方向不代表任何有意义的相位。MVL的计算公式如下:
其中n为数据点总数,t为一个数据点,at为数据点t的振幅,θt为数据点t的相位角。这一方法附带三个警告:(1)值依赖于高频振幅的一般绝对振幅(独立于离群值);(2)振幅异常值对MVL有较大的影响;(3)相位角往往不是均匀分布的。所有的警告都可以被非参数置换检验抵消。在引言中引用的结论之一发现MVL是幅度依赖的问题。然而,这只适用于原始的,而不是置换的MVL。为了完整性起见,Özkurt和Schnitzler提出了一种直接的MVL,它是幅值归一化的,范围在0到1之间。当对MVL和直接MVL应用置换检验时,返回的值基本上是相同的。也就是说,当与置换检验一起应用时,两种测量都是可互相替代的。在没有置换检验的情况下,建议使用直接MVL,因为它考虑了原始数据中可能的振幅差异。
Tort等人的调制指数(MI)
Tort等人提出了一种非常不同的计算相位幅值耦合的方法,但不管怎样,它都是基于相同参数的解析信号、幅值大小和相位角。根据Tort等人计算的MI,−180°到180°所有可能的相位首先分箱(bin)为随意选择的数量。Tort等人使用18个bins,每个20度,之后很多作者也参考这个值。Bins的数量会影响结果,下文将对此进行解释。低频相位的每个相位bin中,高频振幅的平均幅值由下式计算并归一化:
其中,ā为单个bin的平均振幅,k为bins的运行指数,N为bins的总数;p是一个有N个值的向量。在这些计算的帮助下,我们得到了相位幅值图的数据,它以图形的方式描绘了实际的相位幅值耦合(图1B,右内面板)。
随后计算香农熵,表示一个变量的固有信息量的一种度量。如果Shannon熵不是最大的,则该变量具有冗余性和可预测性。当每个相位bin的振幅相等,Shannon熵最大(均匀分布,图1B,右内面板)。香农熵的计算公式如下:
其中p是每个相位bin的归一化的平均振幅的向量,N是bins的总数。如果以后要应用置换检验,那么使用哪个对数基数并不重要。香农熵依赖于使用的bins的数量,这就是MI同样依赖于bins的数量的原因。Bins的数量越大,香农熵可以变得越大。根据最初的研究和其他大多数研究,这里使用了18个bins。
相位振幅耦合的定义是一个明显偏离均匀分布的分布。Kullback-Leibler距离是两个分布的差别的度量,计算公式如下:
其中U为均匀分布,X为数据分布,N为bins的总数,H(p)为根据式4得出的香农熵。均匀分布用log(N)表示。最终的原始MI由以下公式计算:
式中,KL(U, X)为根据式5求得的Kullback-Leibler距离,N为bins总数。
Kramer和Eden的GLM-CFC
对于这个测量,使用数学函数(连接函数:这里是对数连接函数),用一组预测变量(指的是低频相位)来预测一组响应变量(指的是高频振幅)。GLM扩展了线性回归模型,允许响应变量的非正态分布(例如伽马分布)和非线性连接函数(例如,对数连接函数)。因此,它们最适合于相位-振幅耦合:相位和振幅确实呈现非线性关系,瞬时振幅值(从振幅包络线中提取)总是实数和正值,这在伽马分布(而不是正态分布)中得到最好的反映。
在计算GLM-CFC时,从低频滤波的解析信号中提取相位,从高频滤波的解析信号中提取幅值。然后可以在散点图中描绘相位和振幅值(比较图1B,右外面板)。如果数据中存在相位幅值耦合,则在某一相位值时幅值特别高。如果没有相位幅值耦合,振幅值在所有可能的相位值上是相当相似的。在这种情况下,水平线是数据最好的模型,而相位值没有预测能力。如果数据中存在相位-幅值耦合,遵循幅值模式的曲线(三阶多项式)是最好的数据模型。
在相位振幅耦合的情况下,曲线--样条模型(图1B中的红线,右外面板)不同于没有耦合的水平线--零模型(图1B中的黑线,右外面板)。在没有相位幅值耦合的情况下,样条模型与零模型几乎没有差别。也就是说,样条模型与零模型的差异越大,数据中出现的相幅耦合越多。事实上,GLM-CFC发现了两个模型之间的最大绝对差异,并将此差异计算为百分比变化。
模型曲线非常类似于三阶多项式。然而,使用的不是多项式,而是放置在控制点之间的一组样条,它们在-pi和pi之间均匀间隔。这组样条更容易计算,而且它的特性可以比多项式更好的控制。另一方面,引入一种自由度(控制点的数量),这可能会影响结果。因此Kramer和Eden纳入了Akaike信息标准(AIC)的评价,以确定最优控制点的数量。
置换检验
为了量化导出值的意义,所有方法都要经过置换检验。对于置换检验,将观察到的耦合值与洗牌耦合值的分布进行比较。通过计算原始相位时间序列和置换幅值时间序列(反之亦然)之间的耦合值来构造洗牌耦合值。随机在幅值时间序列某数据点上将数据分为两部分,并将两部分的顺序颠倒,构造出置换幅值时间序列。这种生成替代数据的方法是最保守的,因为它保留了脑电图数据的所有特征,除了所研究的相位角和幅值之间的时间关系。洗牌通常重复200-1000次(这里我们使用1000次结果更稳定)。将观察到的耦合值标准化为洗牌耦合值的分布,公式如下:
其中CV为耦合值,µ为平均值,σ为标准差(SD)。只有当观察到的CV大于95%的洗牌值(可以假设洗牌后的幅值时间序列和相位时间序列没有相关)时,才被定义为显著。
统计分析
显著性水平设为p<0.05。对显著性结果进行进一步的事后分析,采用Dunn多重比较程序或事后t检验。报告显著结果的效果量ω2。
相位振幅耦合测量的特异性
在第一步中,通过将调制强度设为I = 0,模拟了5000个没有耦合的数据集。分别对频率对5-7 Hz(相位时间序列)/ 33-47 Hz(幅值时间序列)和8-10 Hz(相位时间序列)/50 -70 Hz(幅值时间序列)进行了仿真。每个数据集的数据长度(400,2500,5000 ms),采样率(500,1000 Hz)和噪声水平(90,100,110%)有所不同,结果总共有90,000个数据集进行耦合计算。相位-振幅耦合值一般采用4 × 3 × 2 × 3方差分析(ANOVA),对PLV、MVL、MI、GLM-CFC四个指标采用重复测量方差分析,比较数据长度(400、2500、5000 ms)、采样频率(500、1000 Hz)和噪声水平(90、100、110%)。
如上所述,执行了非参数置换检验。对原始的相位幅值耦合值进行了z标准化。z值1.64对应的p值为5%。
测量的特异性通过计算假阳性(根据之前分析中发现的显著临界z值)来分析,这取决于(1)方法,(2)数据长度,(3)采样率和(4)噪声水平。为了能够进行方差分析,5000个模拟被分为100个子样本。对每个子样本的假阳性进行计数。采用4 ×3 × 2 × 3重复测量方差分析,自变量是(PLV、MVL、MI、GLM-CFC)、数据长度(400、2500、5000 ms)、采样率(500、1000 Hz)和噪声水平(90、100、110%),因变量假阳性率。
相位振幅耦合的敏感性作为调节变量的函数
通过模拟100个独立数据集,并修改每个数据集的参数(1)调制强度、(2)调制宽度、(3)多模态、(4)数据长度、(5)采样率和(6)噪声水平,量化了相位-幅度耦合测量的性能。计算6个两因素方差分析。每个方差分析包括重复测量因子指标类型,并分别结合重复测量因子调制强度(90、100、110%)、调制宽度(一个低频周期的22.5、25.0、27.5%)、多模态(单相、双相)、数据长度(400、2500、5000 ms)、采样率(500、1000 Hz)、噪声等级(90,100,110%)。
3.结果
相位幅值耦合测量的特异性Theta-低gamma耦合(5-7Hz--33-47Hz)
相位-幅值耦合值不随数据长度、采样率或噪声水平而变化。由于大量的模拟(n = 5000),一些其他的主效应和交互作用变得显著。但所有效应量均ω2<0.01,因此这些差异可以忽略不计。相位-振幅耦合值随计算方法的不同而不同(F(3,14997) = 4471.38, p < 0.01,ω2 = 0.40)。事后t检验显示GLM-CFC(均值±SE:0.29±0.00)显著大于其他所有方法[PLV:0.02±0.00,t(4999) = 74.75, p<0.01,ω2= 0.36;MVL:0.02±0.00,t(4999) = 78.09,p<0.01,ω2=0.38;MI:0.00±0.00,t(4999) = 187.48, p<0.01,ω2= 0.78],其他方法之间差异不显著(ω2<0.01)。当将PLV的临界z值设为1.91,MVL设为1.91,MI设为1.94,GLM-CFC设为2.08时,有5%的模拟数据被错误地归类为有耦合。因此,这些值被定义为临界z值。这意味着PLV和MVL的特异性最高,MI次之,GLM-CFC的特异性最低。根据之前建立的临界z值,假阳性的数量确实因数据长度的不同而不同(F (2,198) = 35.57, p < 0.01,ω2= 0.19,Dunncrit = 0.14)。与中数据段(2500 ms:2.36±0.04)和长数据段(5000 ms:2.32±0.05)相比,在短数据段(400 ms;2.77±0.04)中会有更多的假阳性。中数据段和长数据段的假阳性率没有差异。采用数据长度与计算方法的交互来确定主效应(F (6594) = 51.66, p < 0.01,ω2=0.20,Dunncrit = 0.20),发现上述模式是由PLV和MVL驱动的。MI和GLM-CFC的假阳性率无差异。
alpha -高gamma耦合(8-10Hz--50-70Hz)
相位-振幅耦合值不随数据长度、采样率或噪声水平而变化。由于大量的模拟(n = 5000),一些其他的主效应和交互作用变得显著。但所有效应量均ω2 < 0.01,因此这些差异可以忽略。相位-振幅耦合值随方法的不同而不同(F(3,14997) = 3959.41, p < 0.01,ω2 = 0.37)。事后t检验发现,GLM-CFC(0.24±0.00)显著大于其他所有方法(PLV: 0.01 ± 0.00, t(4999) = 70.29,p < 0.01, ω2 = 0.33; MVL: 0.01 ± 0.00, t(4999) = 75.56,p < 0.01, ω2 = 0.36; MI: 0.00 ± 0.00, t(4999) = 161.05,p < 0.01, ω2 = 0.72),其他方法之间差异不显著(ω2<0.01)。
图2显示了alpha-高gamma耦合的PLV、MVL、MI和GLM-CFC的相位幅值分布。当将PLV的临界z值设置为1.86,MVL的临界z值设置为1.87,MI的临界z值设置为1.97,GLM-CFC的临界z值设置为2.05时,5%的模拟数据被错误地归类为有耦合。因此,这些值被定义为临界z值。这表明PLV和MVL的特异性最强,MI次之,GLM-CFC的特异性最低。
根据之前建立的临界z值,假阳性的数量确实因数据长度的不同而不同(F(2,198) = 4.72, p < 0.01, ω2 = 0.02, Dunncrit = 0.17)。与中段数据和长段数据相比,短段数据中假阳性明显更多。中段数据和长段数据的假阳性率没有差异。采用数据长度与计算方法的交互作用确定了主效应(F(6,594) = 13.28, p < 0.01, ω2 = 0.06, Dunncrit = 0.18),发现上述模式是由PLV和MVL驱动的,MI和GLM-CFC的假阳性率无差异。
图2 零假设下耦合值的概率分布:锁相值(左外板)、MVL(左内板)、MI(右内板)、GLM-CFC(右外板)。这些分布允许定义显著性阈值。红线表示临界的相位幅值耦合z值(5%)。相反,选择一个绝对的截线将导致最小的MVL假阳性,其次是PLV。GLM-CFC检测出的假阳性最多,其次是MI。
相位振幅耦合的敏感性作为调节变量的函数
计算方法对相位-振幅耦合测量的影响
Theta-低gamma耦合(5–7Hz--33–47 Hz)
PLV(1.22±0.05)和MVL(1.53±0.06)与MI(7.83±0.49)的绝对值差异不受其他因素的影响(主效应: F(3,297) = 220.33,p < 0.01, ω2 = 0.62, Dunncrit = 0.78)。PLV和MVL没有区别。GLM-CFC(3.91±0.18)与其他方法不同。
Alpha-高gamma耦合(8–10Hz--50–70 Hz)
PLV(1.77±0.06)和MVL(2.22±0.08)与MI(13.35±0.78)的绝对值差异不受任何其他因素的影响(主效应:F(3,297) = 250.07,p < 0.01, ω2 = 0.65, Dunncrit = 1.28)。PLV和MVL没有区别。GLM-CFC(5.52±0.23)与其他方法不同。
调制强度对相位-振幅耦合方法的影响
Theta-低gamma耦合 (5–7Hz--33–47Hz)
所有方法的耦合值都随调制强度的增大而增大(F(2,198) = 204.74, p < 0.01, ω2 = 0.58)。调制强度与计算方法的交互作用显著(F(6,594) = 154.84, p < 0.01, ω2 = 0.43)。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。调制强度对GLM-CFC的影响最大(0.31 <ω2 < 0.61),其次是MVL(0.21 <ω2 < 0.55)和MI(0.33 <ω2 < 0.54)。PLV对调制强度的敏感性最低(0.15 <ω2 < 0.50)。
Alpha-高gamma耦合(8–10 Hz--50–70 Hz)
所有方法的耦合值都随调制强度的增大而增大(F(2,198) = 215.60, p < 0.01, ω2 = 0.59)。调制强度与计算方法的交互作用显著(F(6,594) = 167.31, p < 0.01, ω2 = 0.45; Figure 3A)。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。调制强度对GLM-CFC(0.36 <ω2 < 0.66)和MVL (0.32<ω2<0.66)影响最大,其次为MI (0.33<ω2<0.57)。PLV对调制强度的敏感性最低(0.20 <ω2 < 0.60)。
耦合越强,PLV、MVL、MI和GLM-CFC越大。正如Tort等人所表明的,这种情况不是所有相位振幅耦合方法所固有的。由于研究人员不仅要证明相幅耦合的存在,而且要区分它的强度,因此能够做到这一点的方法是必不可少的。在所有四种方法中,GLM-CFC在不同调制强度因子水平上的区分效果最好,其次是MVL和MI。
调制宽度度对相位-振幅耦合方法的影响
Theta-低gamma耦合(5–7 Hz-33–47 Hz)
所有方法的耦合值都随调制宽度的增大而增大(F(2,198) = 118.61, p < 0.01, ω2 = 0.44)。调制宽度与计算方法的交互作用显著(F(6,594) = 79.45, p < 0.01, ω2 = 0.28)。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。调制宽度对MVL的影响最大(0.19 <ω2 < 0.51),其次是PLV (0.22 <ω2 < 0.48)。MI (0.15 <ω2 < 0.44)和GLMCFC (0.11 <ω2 < 0.45)对调制宽度的敏感性最小。
Alpha-高gamma耦合(8–10Hz--50–70 Hz)
所有方法的耦合值都随调制宽度的增大而增大(F(2,198) = 145.07, p < 0.01, ω2 = 0.49)。调制宽度与计算方法的交互作用显著(F(6,594) = 103.84, p < 0.01, ω2 = 0.34; Figure 3B)。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。调制宽度对MVL的影响最为明显,其次是PLV (0.10 <ω2 < 0.54)和GLM-CFC (0.11 < ω2 < 0.53)。MI对调制宽度最不敏感(0.12 <ω2 < 0.47)。
耦合宽度越宽,PLV、MVL、MI和GLM-CFC值越大。在所有四种方法中,MVL在调制宽度的不同因素水平之间区分最好。
图3:调制强度和宽度的敏感性:
(A)调制强度效应和(B)调制宽度效应各方法的平均(±SEM)相位幅度耦合值。所有方法的耦合值都随调制强度的增大而增大。然而,除了GLM-CFC, MVL在不同的调制强度因子水平之间区分最好。所有方法的耦合值都随调制宽度的增大而增大。在这里,PLV和MVL在调制宽度的不同因素水平之间区分最好。红线表示临界z值(显著性水平)。这条线以上的所有值表示显著的相位振幅耦合。对于每个效应,根据事后t检验,计算方法内的所有因子水平之间存在显著差异。
多模态对相位-振幅耦合方法的影响
Theta-低gamma耦合(5–7Hz--33–47 Hz)
单相耦合(4.89±0.24)比双相耦合总体上更强(2.36 ± 0.15;F(1,99) = 586.81, p < 0.01, ω2 = 0.75)。模态与计算方法的交互作用显著(F(3,297) = 73.81, p < 0.01,ω2 = 0.21)。PLV(2.42±0.10 vs. 0.02±0.01; t(99) = 25.20, p < 0.01, ω2 = 0.76)和MVL(3.04±0.12 vs. 0.02±0.01; t (99) = 25.54, p < 0.01,ω2 = 0.77)检测不到双相耦合。MI的单相耦合大于双相耦合(9.24 ± 0.53 vs. 6.41 ± 0.45; t(99) = 18.54, p < 0.01,ω2 = 0.63)。GLM-CFC在单相耦合中也比在双相耦合中更大(4.86 ± 0.22 vs. 2.96 ± 0.14; t(99) = 21.90,p < 0.01,ω2 = 0.71)。
Alpha-高gamma耦合(8–10Hz-50–70 Hz)
单相耦合(7.54±0.34)比双相耦合总体上更强(3.89 ± 0.23;F(1,99) = 782.07, p < 0.01, ω2 = 0.80)。模态与计算方法的交互作用显著(F(3,297) = 74.41, p < 0.01,ω2 = 0.22)。PLV(3.52 ± 0.12 vs. 0.02 ± 0.01; t(99) = 29.27, p < 0.01, ω2 = 0.81)和MVL(4.41 ± 0.15 vs. 0.02 ± 0.01; t(99) = 29.57, p < 0.01,ω2 = 0.81)检测不到双相耦合。MI的单相耦合大于双相耦合(15.40 ± 0.83 vs. 11.29 ± 0.74; t(99) = 19.22, p < 0.01,ω2 = 0.65)。GLM-CFC在单相耦合中也比在双相耦合中更大(6.83 ± 0.28 vs. 4.22 ± 0.19; t(99) = 24.78,p < 0.01, ω2 = 0.75; Figure 4A)。
也就是说,模态对四种方法的影响是非常不同的。PLV和MVL无法检测到双相耦合。由于MVL的数学表达(方程2, Figure 1B),这并不奇怪。在极平面上,峰和谷出现在相对的两侧:它们的均值会相互抵消。如果存在其他形式的双相耦合,MVL可以找到它,但可能会低估它的强度,并进一步返回扭曲的相位信息。因此,在解释结果之前,看一看极坐标图是很重要的。类似地,PLV不能检测双相耦合。对于双相耦合,波幅包络振荡速度是低频带的两倍。因此,上下频带之间的相位滞后横跨整个极平面。MI和GLM-CFC能够找到双相耦合,但双相耦合导致相幅耦合值降低;这种不希望发生的降低,GLM-CFC比MI更强烈。以往文献表明,双相耦合在实证数据中起很次要的作用。据我们所知,只有非常小的一部分研究使用了双相耦合。大多数研究都使用了单相耦合。
数据长度对相位-振幅耦合方法的影响
Theta-低gamma耦合(5–7Hz-33–47 Hz)
所有方法的耦合值随数据长度的增加而增加(数据长度的主效应:F(2,198) = 390.95, p < 0.01,ω2 = 0.72)。在最短的400毫秒内,没有一种方法可以检测到显著的耦合,即使在数据里设置了耦合。数据长度与计算方法的交互作用显著(F(6,594) = 251.91, p < 0.01, ω2 = 0.56)。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。MVL (0.60 <ω2 < 0.85)和PLV (0.57 <ω2 < 0.83)的数据长度效应最为显著,其次是GLM-CFC(0.56 <ω2 < 0.77)。数据长度对MI的影响最小(0.46 <ω2 < 0.62)。
Alpha-高gamma耦合(8–10Hz-50–70 Hz)
所有方法的耦合值随数据长度的增加而增加(数据长度的主效应:F(2,198) = 422.16, p < 0.01,ω2 = 0.74)。在最短的400毫秒内,没有一种方法可以检测到显著的耦合,即使在数据里设置了耦合。数据长度与计算方法的交互作用显著。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。MVL(0.75 <ω2 < 0.87)和PLV (0.73 <ω2 < 0.86)的数据长度效应最为显著,其次是GLM-CFC(0.66 <ω2 < 0.79)。数据长度对MI的影响最小(0.54 <ω2 < 0.62)。
总的来说,数据越长,PLV、MVL、MI和GLM-CFC耦合值越大。这种关联在本文模你的数据中虽然出现,但不能普遍适用。本文中耦合是连续地模拟到数据中的。如果耦合是瞬时的,并且不随数据长度成比例变化,则不需要应用此关系。潜在的一般规则是,耦合发生的数据越长,相位振幅耦合值就越强。这应该在后续分析中进行测试。该分析进一步表明,发现耦合所需的最小数据长度,当包括30个试次时,每个试次应至少应超过400毫秒。没有一种方法能够在最短的模拟时间400毫秒内检测到耦合。对于数据长度开发一个校正因子可能是有用的(例如,类似于对数据长度变化不敏感的成对相位一致性[pairwise phase consistency]),使相位振幅耦合值在各个研究中更具可比性。在四种方法中,混淆因子数据长度对MI的影响最小。
采样率对相位-振幅耦合方法的影响
Theta-低gamma耦合(5–7Hz- 33–47 Hz)
采样率对任何相幅耦合值[F(1,99) = 0.10, p = 0.75]均无影响,也没有交互效应。
Alpha-高gamma耦合(8–10Hz -50–70 Hz)
总体的耦合值随采样率的增加略有增加(F(1,99) = 38.65, p < 0.01, ω2 = 0.16)。采样率的效应因计算方法不同而不同(F(3,297) = 27.80,p < 0.01, ω2 = 0.09; Figure 4C)。对GLM-CFC (t(99) = 6.26, p < 0.01,ω2 = 0.16)影响最大,其次为MI(t(99) = 5.71, p < 0.01,ω2 = 0.14)。对PLV影响最小。
采样率因其对theta-低gamma耦合的影响不足而对alpha-高gamma耦合的影响较小而显得突出。第三组数据模拟测试了调制频率为16-18 Hz和调制频率为202-238 Hz时的PLV、MVL和MI。这一分析表明,采样率确实很重要,但只有在研究的上频带范围接近Nyquist频率时才有影响。四种方法中,MVL和PLV受采样率的影响最小。
噪声对相位-振幅耦合方法的影响
Theta-低gamma耦合(5–7Hz--33–47 Hz)
所有方法的耦合值随噪声的增大而减小(F(2,198) = 372.07, p < 0.01,ω2 = 0.71)。噪音与计算方法的交互作用显著。事后t检验表明,同一方法内各因子水平差异显著(p均< 0.01)。噪声对GLM-CFC的影响最为明显(0.65 < ω2 < 0.75)。MVL (0.42 < ω2 < 0.70)和MI(0.53 < ω2 < 0.62)为中度。PLV(0.30 < ω2 < 0.65)受噪声影响最小。
Alpha-高gamma耦合(8–10Hz -50–70 Hz)
所有方法的耦合值随噪声的增大而减小(F(2,198) = 417.74, p < 0.01,ω2 = 0.74)。噪声与计算方法的交互作用显著。噪声对GLM-CFC的影响最为明显(0.67 < ω2 < 0.79)。MVL (0.50 < ω2 < 0.80)和MI(0.55 < ω2 < 0.66)为中度。PLV(0.44 < ω2 < 0.74)受噪声影响最小。
总体而言,数据噪声越大,PLV、MVL、MI和GLM-CFC越小。这一方面不是我们所希望的,但却是可信的。噪声模糊了低频的相位和高频的幅值之间的关系。四种方法中,GLM-CFC方法效果最好,PLV受噪声影响最小。MVL比MI受影响更大。
图4:相位幅值耦合的调节测量:对于(A)多模态效应、(B)数据长度效应、(C)采样率效应和(D)噪声效应,每种方法的平均(±SEM)相位幅值耦合值。
交互作用效果
对每种方法分别进行六个方向的方差分析,揭示了所有因素(模态、数据长度、采样率、噪声、调制强度和调制宽度)的作用。特别是模态和数据长度与剩余因子的交互作用。采样率仅当分析频率接近 Nyquist频率时才显示出显著的交互作用。例如,MVL随着数据长度的增加而增加,但是当噪声增加时,MVL的增加就会减少(图5)。这种模式适用于每一个增加的因素。锁相值和MVL均未发现双相耦合。因此,对于这两种方法,所描述的主效应和交互作用模式只适用于单相,而不适用于双相耦合。对于MI和GLM-CFC,这种模式适用于单相和双相耦合。
我们的经验表明,这些方法与选择的频带组合无关。据我们所知,这些方法的频率依赖性没有数学上的原因。
与其他三种方法相比,GLM-CFC的调制强度最佳,对噪声最差。从其他因素看,其性能处于中等范围。GLM-CFC最重要的缺点是计算时间非常长,超过其他方法2个数量级(不计算置信区间),最多超过4个数量级(计算置信区间)。增加数据点会以类似的方式增加所有方法的计算时间(例如,数据点增加一倍,计算时间就增加一倍)。
通过对其他三种方法的比较,可以看出MI受多模态和数据长度的影响最小。然而,与MVL相比,它也像PLV一样对调制强度的变化不太敏感。与MVL和PLV相比,MI对调制宽度的敏感性更低。受到噪声的影响时,MVL和MI相似,且比PLV更强。
图5 相幅耦合MVL的调节变量之间的交互作用。交互作用有一个单调的模式。MVL随数据的正常而增加,但当噪声增加时,它的增加变少。这种模式适用于每一个增加的因素。红线表示临界z值(显著性水平)。这条线以上的所有值表示显著的相位振幅耦合。Dunn事后检验表明,每种方法各因子水平均存在显著差异。只有在400毫秒条件下的值在噪音水平之间没有差异。
4. 结论
对于长数据段,高采样率,高信噪比,建议使用MVL,因为它对调制强度和宽度比其他两种方法更敏感。对于更高噪声的数据,更短的数据,更低的采样率,建议使用MI,因为与其他两种方法相比,它受混杂因素的影响最小。如果不清楚跨频耦合是单相的还是双相的,就应该使用MI,尽管文献表明双相耦合可以忽略。
与其他两项指标相比,PLV并不突出。到目前为止,没有一项审查明确评价这一方法是积极的。它的使用可能存在问题,因为相位信息是从信号的波幅包络中提取的。相位信息只能从真正的振荡信号中正确提取;波幅包络不一定是这样。但是这个缺点可以通过先对振幅包络进行滤波,然后再从它提取相位信息来抵消。
由于MVL和MI具有互补的优点和缺点,因此对两者都进行计算是明智的。测量这两种方法的耗时方面是置换检验。另一方面,计算这两种指标不会大幅增加分析时间。
MI在数量上大于PLV和MVL。然而,即使在数值上有很大的定量差异,对于我们模拟中的所有四种方法从定性上来说,相位幅值耦合的重要性是相同的。计算方法之间的耦合强度的比较是有问题的,这种缺乏可比性提供了同时报告MVL和MI二者的另一个原因。
与MVL相比,MI的假阳性率不受任何混杂因素的影响。然而,MVL的这优势被一个MVL的劣势抵消了:MI的计算包括香农熵。熵值取决于bins的数量以及分到相同数量bins中的数据量。这是一个不良的自由度,但在计算MVL时不存在。
由于对混杂变量(如数据长度)的依赖,即使使用相同的方法,也很难比较各个研究的绝对耦合强度。另一方面,在一项研究中进行比较还是可以的。然而,应该确保在所有实验条件下和整个实验过程中信噪比是可比较的。
一般来说,建议通过置换检验使用标准化的相位振幅耦合测量法。它有助于对测量的解释。
Kramer和Eden指出,“目前还不存在评估跨频率耦合(CFC)的最佳分析方法”。即使某个计算方法很理想,较少受到混淆因素的影响,但至少要报告2种合理的计算方法从而使结论更可靠。
如需原文及补充材料或需要跨频率耦合数据分析请添加思影科技微信:siyingyxf或18983979082获取,如对思影课程及服务感兴趣也可加此微信号咨询。另思影提供免费文献下载服务,如需要也可添加此微信号入群,原文也会在群里发布,如果我们的解读对您的研究有帮助,请给个转发支持以及右下角点击一下在看,是对思影科技莫大的支持,感谢!