numpy序列预处理dna序列_使用GAN生成时间序列数据，DoppelGANger论文详解

序列数据(具有时间依赖性的数据)在业务中非常常见，从信用卡交易到医疗保健记录再到股票市场价格。 但是，隐私法规限制并极大地减慢了对研发至关重要的有用数据的访问。 这就产生了对具有高度代表性但又完全私有的合成顺序数据的需求，这至少可以说是具有挑战性的。

生成合成时间序列和顺序数据要比表格数据更具挑战性，在表格数据中，通常将与一个人有关的所有信息存储在一行中。 在顺序数据中，信息可以分布在许多行中，例如信用卡交易，并且保留行(事件)和列之间的相关性(变量是关键)。 此外，序列的长度是可变的。 有些案例可能只包含少量交易，而其他案例则可能包含数千笔交易。

序列数据和时间序列的生成模型已经得到了广泛的研究，但是，许多此类努力导致综合数据质量相对较差且灵活性较低。 在许多情况下，模型被设计为特定于每个问题，因此需要详细的领域知识。

在本文中，我们描述并应用了一种最新的强大方法的扩展版本，以生成合成顺序数据DoppelGANger。 它是基于生成对抗网络(GAN)的框架，具有一些创新，使生成复杂顺序数据集的合成版本成为可能。

我们通过引入两项创新来构建这项工作：

1. 一种学习策略，可加快GAN的收敛速度并避免模式崩溃。

1. 鉴别器中经过精心设计的噪声可使用差异会计处理策略的改进版本来提高模型的稳定性，从而使过程具有不同的私有性而不会降低数据质量。

时序数据生成的常用方法

用于时序数据生成的大多数模型都使用以下方法之一：

动态平稳过程通过将时间序列中的每个点表示为确定性过程的总和(加上一些噪声)而起作用。 这是使用自举等技术对时间序列进行建模的一种广泛使用的方法。 但是，必须纳入一些长期依赖性的先验知识，例如循环模式，以约束确定性过程。 这使得很难为具有复杂，未知相关性的数据集建模。

马尔可夫模型是一种通过将系统动力学表示为条件概率分布来对分类时间序列建模的流行方法。 诸如隐马尔可夫模型的变体也已用于对时间序列的分布进行建模。 这种方法的问题在于它无法捕获长期的复杂依赖关系。

自回归(AR)模型是动态平稳过程，其中序列中的每个点都表示为前n个点的函数。非线性AR模型(如ARIMA)非常强大。像马尔可夫模型那样的AR模型存在保真度问题-它们产生的简单模型无法捕获复杂的时间相关性。

递归神经网络(RNN)最近已用于深度学习中的时间序列建模。像自回归模型和马尔可夫模型一样，RNN使用以前时间步长的滑动窗口来确定下一个时间点。 RNN还存储一个内部状态变量，该变量捕获时间序列的整个历史记录。像长短期记忆网络(LTSM)一样，RNN在学习时间序列数据的判别模型方面也取得了巨大的成功，该模型可预测以样本为条件的标签。但是，RNN无法学习某些简单的时间序列分布。

基于GAN的方法或生成对抗网络模型已经成为一种流行的技术，用于生成或扩充数据集，尤其是图像和视频。但是，GAN在网络数据中保真度较差，网络数据既具有复杂的时间相关性，又具有混合的离散连续数据类型。尽管存在基于GAN的时间序列生成(例如，用于医疗时间序列)，但此类技术无法处理更复杂的数据，这些数据在长序列上显示出较差的自相关评分，同时容易出现模式崩溃。这是由于以下事实：数据分布是重尾且长度可变的。这似乎在很大程度上影响GAN。

引入DoppelGANger以生成高质量的合成时间序列数据

在本节中，我将探索最近的模型以生成综合顺序数据DoppelGANger。 我将使用基于GAN的此模型以及由循环单位组成的生成器，使用两个数据集生成交易数据的综合版本：银行交易和道路交通。 我们使用了对DoppelGANger模型的修改，以解决顺序数据生成模型的局限性。

由于以下问题，传统的生成对抗网络或GAN难以对顺序数据进行建模：

1. 它们没有捕获时间特征及其相关(不变)属性之间的复杂关联：例如，根据所有者的特征(年龄，收入等)，交易中的信用卡模式非常不同。

1. 时间序列内的长期相关性，例如昼夜模式：这些相关性与图像中的相关性在质量上有很大不同，图像具有固定的尺寸，不需要逐像素生成。

DoppelGANger结合了一些创新的想法，例如：

使用两个网络(一个多层感知机 MLP和一个递归网络)捕获时间依赖性

分离归因生成，以更好地捕获时间序列及其属性(例如用户的年龄，位置和性别)之间的相关性

批量生成-生成长序列的小批量堆叠

解耦归一化-将归一化因子添加到生成器以限制特征范围

DoppelGANger将属性的生成与时间序列解耦，同时在每个时间步将属性馈送到时间序列生成器。 这与传统方法相反，在传统方法中，属性和特征是共同生成的。

DoppelGANger的条件生成体系结构还提供了更改属性分布和对属性进行条件调整的灵活性。 这也有助于隐藏属性分布，从而增加隐私。

DoppelGANger模型还具有生成以数据属性为条件的数据特征的优势。

图1：原始DoppelGANger模型的示意图，两个生成器块和两个鉴别器。

该模型的另一个巧妙特征是它如何处理极端事件，这是一个非常具有挑战性的问题。顺序数据在样本中具有广泛的功能值并不少见-有些产品可能有成千上万笔交易，而另一些则只有几笔。对于GAN来说，这是有问题的，因为它肯定是模式崩溃的秘诀-样本将仅包含最常见的项目，而忽略罕见事件。对于图像-几乎所有工作都集中在GAN上-这不是问题，因为分布很平滑。这就是为什么DoppelGANger的作者提出了一种创新的方式来处理这些情况：自动归一化。它包括在训练之前对数据特征进行归一化，并将特征的最小和最大范围添加为每个样本的两个附加属性。

在生成的数据中，这两个属性通常会将要素缩放回现实范围。这分三个步骤完成：

· 使用多层感知器(MLP)生成器生成属性。

· 将生成的属性作为输入，使用另一个MLP生成两个"伪"(最大/最小)属性。

· 将生成的真实和假属性作为输入，生成要素。

将DoppelGANger模型放在银行交易数据上

首先，我们在银行交易数据集上评估了DoppelGANger。 用于训练的数据是合成的，因此我们知道真实的分布，可以在这里访问。 我们的目的是证明该模型能够学习数据中的时间依赖性。

如何准备数据？

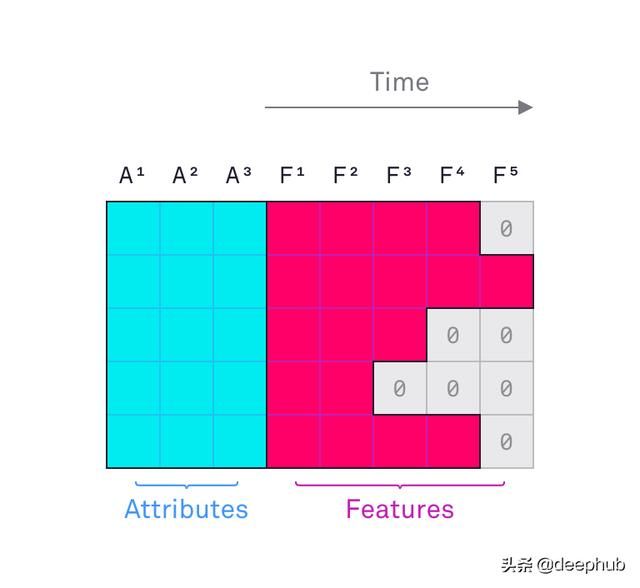
图2：作为一组属性和长度不同的特征处理的数据的示意图。

我们假设顺序数据由一组最大长度为Lmax的序列组成-在本例中，我们认为Lmax =100。每个序列都包含一组属性A(固定数量)和特征F(交易)。 在我们的例子中，唯一的属性是初始银行余额，其特征是：交易金额(正数或负数)以及两个描述交易的其他类别：标志和描述。

要运行模型，我们需要三个NumPy数组：

· data_feature：训练功能，采用NumPy float32数组格式。 大小为[(训练样本数)x(最大长度)x(特征的总尺寸)]。 分类特征通过一键编码存储。

· data_attribute：训练属性，为NumPy float32数组格式。 大小为[(训练样本数)x(属性的总维数)]。

· datagenflag：一组标志，指示功能的激活。 大小为[(训练样本数)x(最大长度)]。

另外，我们需要一个Output类的对象列表，其中包含每个变量，规范化和基数的数据类型。 在这种情况下，它是：

data_feature_outputs = [output.Output(type_=OutputType.CONTINUOUS,dim=1,normalization=Normalization.ZERO_ONE,is_gen_flag=False), # time intervals between transactions (Dif)    output.Output(type_=OutputType.DISCRETE,dim=20,is_gen_flag=False), # binarized Amount    output.Output(type_=OutputType.DISCRETE,dim=5,is_gen_flag=False),# Flagoutput.Output(type_=OutputType.DISCRETE,dim=44,is_gen_flag=False) # Description    ]

列表的第一个元素是事件Dif之间的时间间隔，其后是经过1个热编码的交易值(金额)，然后是标志，第四个元素是交易描述。 所有gen_flags都设置为False，因为它是一个内部标志，以后可以由模型本身进行修改。

该属性被编码为介于-1和1之间的归一化连续变量，以解决负余额问题：

data_attribute_outputs = [output.Output(type_=OutputType.CONTINUOUS,dim=1,normalization=Normalization.MINUSONE_ONE,is_gen_flag=False)]

此模拟中使用的唯一属性是初始余额。 每个步骤的余额只需添加相应的交易金额即可更新。

我们使用Hazy处理器对每个序列进行预处理，并以正确的格式对其进行整形。

n_bins = 20processor_dict = {            "by_type": {                  "float": {                    "processor": "FloatToOneHot", #FloatToBin"                    "kwargs": {"n_bins": n_bins}                  },                  "int": {                    "processor": "IntToFloat",                    "kwargs": {"n_bins": n_bins}                  },                  "category": {                    "processor": "CatToOneHot",                  },                 "datetime": {                    "processor": "DtToFloat",                  }                }        }from hazy_trainer.processing import HazyProcessorprocessor = HazyProcessor(processor_dict)

现在，我们将读取数据并使用formatdata函数对其进行处理。 辅助变量categoryn和category_cum分别存储变量的基数和基数的累积和。

data=pd.read_csv('data.csv',nrows=100000)    # read the datacategorical = ['Amount','Flag','Description'] continuous =['Balance','Dif']cols = categorical + continuousprocessor = HazyProcessor(processor_dict) #call Hazy processorprocessor.setup_df(data[cols]) # setup the processorcategories_n = [] # Number of categories in each categorical variablefor cat in categorical:    categories_n.append(len(processor.column_to_columns[cat]['process']))categories_cum = list(np.cumsum(categories_n)) # Cumulative sum of number of categorical variablescategories_cum = [x for x in categories_cum] # We take one out because they will be indexescategories_cum = [0] + categories_cumdef format_data(data, cols, nsequences=1000, Lmax=100, cardinality=70):''' cols is a list of columns to be processednsequences  number of sequences to use for training   Lmax is the maximum sequence length   Cardinality shape of sequences'''   idd=list(accenture.Account_id.unique()) # unique account ids   data.Date = pd.to_datetime(data.Date) # format date  # dummy to normalize the processors data['Dif']=np.random.randint(0,30*24*3600,size=accenture.shape[0])    data_all = np.zeros((nsequences,Lmax,Cardinality))   data_attribut=np.zeros((nsequences))   data_gen_flag=np.zeros((nsequences,Lmax))   real_df = pd.DataFrame()   for i,ids in enumerate(idd[:nsequences]):      user = data[data.Account_id==ids]      user=user.sort_values(by='Date')      user['Dif']=user.Date.diff(1).iloc[1:]       user['Dif']=user['Dif'].dt.seconds       user = user[cols]      real_df=pd.concat([real_df,user])      processed_df = processor.process_df(user)      Data_attribut[i] = processed_df['Balance'].values[0]      processed_array = np.asarray(processed_df.iloc[:,1:)      data_gen_flag[i,:len(user)]=1      data_all[i,:len(user),:]=processed_arrayreturn data_all, data_attribut, data_gen_flag

数据

数据包含大约1000万笔银行交易，我们将仅使用其中包含5,000个唯一帐户的100,000个样本，每个帐户平均20个交易。 我们考虑以下领域：

1. 交易日期

1. 交易金额

1. 平衡

1. 交易标记(5级)

1. 描述(44级)

以下是所用数据的标题：

表1：银行交易数据样本

如前所述，时间信息将被建模为两个连续事务之间的时间差(以秒为单位)。

图3：不同描述的交易直方图按收入和支出分开。

图4：不同时间分布的交易热图。

图5：交易金额的分布。

图6：初始余额的分布。 请注意，由于透支，某些账户的初始余额为负。

图7：一个月内的交易数量-收入和支出。 请注意，收入有非常明显的峰值。 综合数据必须捕获这些峰

运行代码

我们使用以下参数仅运行了100个轮次的代码：

import sysimport ossys.path.append("..")import matplotlib.pyplot as pltfrom gan import outputsys.modules["output"] = outputimport numpy as npimport pickleimport pandas as pdfrom gan.doppelganger import DoppelGANgerfrom gan.load_data import load_datafrom gan.network import DoppelGANgerGenerator, Discriminator, AttrDiscriminatorfrom gan.output import Output, OutputType, Normalizationimport tensorflow as tffrom gan.network import DoppelGANgerGenerator, Discriminator,     RNNInitialStateType, AttrDiscriminatorfrom gan.util import add_gen_flag, normalize_per_sample,     renormalize_per_samplesample_len = 10epoch = 100batch_size = 20d_rounds = 2g_rounds = 1d_gp_coe = 10.0attr_d_gp_coe = 10.0g_attr_d_coe = 1.0

请注意，生成器由具有softmax激活函数(用于分类输入)和线性激活(用于连续变量)的层列表组成。 生成器和鉴别器均使用Adam算法以指定的学习速率和动量进行了优化。

现在，我们准备数据以供网络使用。 realattributemask是一个True / False列表，其长度与属性数相同。 如果属性为(max-min)/ 2或(max + min)/ 2，则为False；否则为false。 否则为True。首先我们实例化生成器和鉴别器：

# create the necessary input arraysdata_all, data_attribut, data_gen_flag = format_data(data,cols)# normalise data(data_feature, data_attribute, data_attribute_outputs, real_attribute_mask) = normalize_per_sample(        data_all, data_attribut, data_feature_outputs,        data_attribute_outputs)# add generation flag to featuresdata_feature, data_feature_outputs = add_gen_flag(    data_feature, data_gen_flag, data_feature_outputs, sample_len)generator = DoppelGANgerGenerator(    feed_back=False,    noise=True,    feature_outputs=data_feature_outputs,    attribute_outputs=data_attribute_outputs,    real_attribute_mask=real_attribute_mask,    sample_len=sample_len,    feature_num_units=100,    feature_num_layers=2)discriminator = Discriminator()attr_discriminator = AttrDiscriminator()

我们使用了由两层100个神经元组成的神经网络，用于生成器和鉴别器。 所有数据均经过标准化或1热编码。 然后，我们使用以下参数训练模型：

checkpoint_dir = "./results/checkpoint"sample_path = "./results/time"epoch = 100batch_size = 50g_lr = 0.0001d_lr = 0.0001vis_freq = 50vis_num_sample = 5d_rounds = 3g_rounds = 1d_gp_coe = 10.0attr_d_gp_coe = 10.0g_attr_d_coe = 1.0extra_checkpoint_freq = 30num_packing = 1

训练的注意事项

如果数据很大，则应使用更多的轮次-作者建议使用400个时期，但在我们的实验中，我们发现如果网络不退化和模式崩溃，则可以达到1000个轮次。另外，请考虑时期数与批次大小有关–较小的批次需要更多的时期和较低的学习率。

对于那些不熟悉神经网络的人来说，批处理，随机和Minibatch梯度下降是机器学习算法的三种主要形式。批量大小控制训练神经网络时误差梯度估计的准确性。用户应注意学习期间批次大小，速度和稳定性之间的权衡。较大的批次需要较高的学习率，并且网络将学习得更快，但是它也可能不稳定，这对于GAN来说尤其是因为模式崩溃问题。

根据经验，生成器和鉴别器的学习率应该很小(在10–3到10–5之间)并且彼此相似。在本例中，我们使用10–4，而不是默认的10–3。

另一个重要参数是生成器和鉴别器上的回合数。 Wasserstein GAN(WGAN)需要两个组件才能正常工作：梯度裁剪和比生成器高的鉴别器(dround)。通常，对于发生器的每一轮，鉴别器的轮数在3至5之间。在这里，我们使用dround = 3和g_round = 1。

为了加快训练速度，我们对生成器使用了周期性的学习率，对鉴别器使用了固定的学习率。

目录samplepath存储在不同检查点收集的一组样本，这对于验证目的很有用。 损失函数的可视化可以在您提供的检查点目录上使用TensorBoard完成。 您可以使用参数extracheckpoint_freq控制检查点的频率。

请注意，这可能会占用大量磁盘空间。

run_config = tf.ConfigProto()tf.reset_default_graph() # if you are using spyder with tf.Session(config=run_config) as sess:    gan = DoppelGANger(        sess=sess,         checkpoint_dir=checkpoint_dir,        sample_dir=sample_dir,        time_path=sample_path,        epoch=epoch,        batch_size=batch_size,        data_feature=data_feature,        data_attribute=data_attribute,        real_attribute_mask=real_attribute_mask,        data_gen_flag=data_gen_flag,        sample_len=sample_len,        data_feature_outputs=data_feature_outputs,        data_attribute_outputs=data_attribute_outputs,        vis_freq=vis_freq,        vis_num_sample=vis_num_sample,        generator=generator,        discriminator=discriminator,        attr_discriminator=attr_discriminator,        d_gp_coe=d_gp_coe,        attr_d_gp_coe=attr_d_gp_coe,        g_attr_d_coe=g_attr_d_coe,        d_rounds=d_rounds,        g_rounds=g_rounds,g_lr=g_lr,d_lr=d_lr,        num_packing=num_packing,        extra_checkpoint_freq=extra_checkpoint_freq)    gan.build()    gan.train()

综合数据生成

训练模型后，您可以使用生成器根据噪声创建综合数据。 有两种方法可以做到这一点：

1. 纯噪声无条件生成

1. 属性的条件生成

在第一种情况下，我们生成属性和特征。 在第二种方法中，我们明确指定要使用哪些属性来条件化要素生成，以便仅生成要素。

以下是从中生成样本的代码：

run_config = tf.ConfigProto()total_generate_num_sample = 1000with tf.Session(config=run_config) as sess:    gan = DoppelGANger(        sess=sess,         checkpoint_dir=checkpoint_dir,        sample_dir=sample_dir,        time_path=time_path,        epoch=epoch,        batch_size=batch_size,        data_feature=data_feature,        data_attribute=data_attribute,        real_attribute_mask=real_attribute_mask,        data_gen_flag=data_gen_flag,        sample_len=sample_len,        data_feature_outputs=data_feature_outputs,        data_attribute_outputs=data_attribute_outputs,        vis_freq=vis_freq,        vis_num_sample=vis_num_sample,        generator=generator,        discriminator=discriminator,        attr_discriminator=attr_discriminator,        d_gp_coe=d_gp_coe,        attr_d_gp_coe=attr_d_gp_coe,        g_attr_d_coe=g_attr_d_coe,        d_rounds=d_rounds,        g_rounds=g_rounds,        num_packing=num_packing,        extra_checkpoint_freq=extra_checkpoint_freq)# build the network     gan.build()        length = int(data_feature.shape[1] / sample_len)    real_attribute_input_noise = gan.gen_attribute_input_noise(                total_generate_num_sample)    addi_attribute_input_noise = gan.gen_attribute_input_noise(                total_generate_num_sample)    feature_input_noise = gan.gen_feature_input_noise(                total_generate_num_sample, length)    input_data = gan.gen_feature_input_data_free(                total_generate_num_sample)# load the weights / change the path accordingly    gan.load(checkpoint_dir+'/epoch_id-100')# generate features, attributes and lengths    features, attributes, gen_flags, lengths = gan.sample_from(        real_attribute_input_noise, addi_attribute_input_noise,        feature_input_noise, input_data, given_attribute=None,        return_gen_flag_feature=False)#denormalise accordingly    features, attributes = renormalize_per_sample(        features, attributes, data_feature_outputs,        data_attribute_outputs, gen_flags,        num_real_attribute=1)

我们需要一些额外的步骤来将生成的样本处理为序列格式，并以1-hot编码格式返回向量。

nfloat = len(continuous)synth=np.zeros(features.shape[-1])for i in range(features.shape[0]):    v = np.concatenate([np.zeros_like(attributes[i]), np.zeros_like(features[i])],axis=-1)    v[attributes[i].shape] = attributes[i]    V[attributes[i].shape[0]:attributes[i].shape[0]+1] = feature[i,:,0]    for j, c in enumerate(categories_cum[:-1]):        ac = features[:,nfloat+categories_cum[j]-1:          nfloat+categories_cum[j+1]-1]        a_hot = np.zeros((ac.shape[0], categories_n[j]))            a_hot[np.arange(ac.shape[0]),ac.argmax(axis=1)] = 1        v[:,nfloat+categories_cum[j]:nfloat+categories_cum[j+1]]=a_hot    v=np.concatenate([np.array([i]*len(ac))[np.newaxis].T,v],axis=1)    synth = np.vstack([synth,v])    df = pd.DataFrame(synth[1:,1:],columns=processed_df.columns)formated_df = processor.format_df(df)formated_df['account_id']=synth[:,0] # add account_id

下面我们介绍了合成(生成)数据和真实数据之间的一些比较。 我们可以观察到，总的来说，生成的数据分布与真实数据分布相对匹配-图8和图9。

图8：生成的数据与实际数据之间交易(中间)和标志(底部)之间的序列长度(顶部)时间间隔的直方图。

唯一的例外是变量Amount的分布，如图9所示。这是由于该变量具有不平滑的分布这一事实。 为了解决这个问题，我们将其离散化为20个级别，从而实现了更好的匹配。

图9：使用连续编码(顶部)和二值一次热编码(底部)生成的实数与实数。

然后，我们使用模糊指标来计算相似度得分。 该分数是三个分数的平均值：直方图和直方图2D相似度(实际数据和合成数据直方图重叠的程度)以及列之间的互信息。 该分数确定了综合数据保留列之间相关性的程度。

将Amount视为连续变量时，我们获得的相似度得分为0.57，将其二进制化为20个仓位时，获得的相似度得分为0.63。 相似度得分如下：

from hazy_trainer.evaluation.similarity import Similaritysim = Similarity(metrics=['hist','hist2d','mi'])score = sim.score(real_df[cols], formated_df[cols])print(score['similarity']['score'])

但是，我们注意到，这个数字并不能真正说明整个故事，因为它没有明确衡量合成数据序列的时间一致性，而是独立对待每一行。

图10：模型随时间产生的交易金额(入金和出金)。

为此，我们使用了另一个关键指标：自相关，它测量时间t中的事件与时间t — ∆发生的事件之间的关系，其中∆是时间滞后。 为了测量关系，我们通过以下方式进行比较：

AC = i = 1T(Areali -Asynthetici)2 / i = 1T(Areali)2

以下是在实际数据和综合数据上花费的总金额(按天汇总)的自相关图。 我们可以看到两者具有非常相似的模式。

这仅适用于数值数据。 对于分类，我们可以使用相互信息。 对于我们的数据，我们得到AC = 0.71

图11：银行交易数据集的真实数据和综合数据的自相关。

交通流量数据集

为了证明顺序数据生成器的功能，我们在另一个更具挑战性的数据集上进行了测试：Metro Interstate Traffic Volume Data Set。 这是一个包含2012年至2018年每小时流量数据的数据集。正如我们在下图中看到的那样，该数据随着时间的推移相对一致，具有某些每日和每周的模式以及较大的每小时变化性。 来自生成器的综合数据必须重现所有这些趋势。

图12：交通量(每小时车辆)的直方图。

下图包含第一个月(2012年10月)的流量，其每日模式可能非常复杂：

图14：2012年10月的每小时流量模式。每次下降都代表一天。 周末在低流量模式中可见。

为了生成高质量的合成数据，网络必须预测正确的每日，每周，每月甚至每年的模式，因此长期相关性很重要。

图15：更多数据分布

在自相关方面，我们可以看到平滑的每日相关性-这很有意义，因为大多数流量具有对称行为。 早晨的高强度与晚上的高强度相关。

图15：实际流量数据与生成的流量数据的自相关。 对于更长的分支，合成数据的自相关开始偏离从真实数据获得的相关性

运行模型

在这种情况下，序列长度是固定的。 为了准备数据，我们使用每月和每周数据的滑动窗口生成了50,000个序列。 该数据集比以前的数据集要大得多，我们希望模型能够平稳运行而不会崩溃。

在这种情况下，我们还有更多的属性。 有些是根据数据构建的，例如"星期几"和"月份"：

· 温度

· 雨

· 雪

· 云

· 其他天气情况

· 节日

· 一周中的week

· 月

作为功能，我们只有每小时的流量。 由于我们要捕获具有最高粒度的变量，因此将所有数值离散化为20个bin，但将流量离散化为50个bin。 该模型运行了200个轮次，批次大小为20，学习率与以前相同。

结果

图17包含一个真实的和生成的样本。 我们可以看到，循环模式保持得很好，数据看起来很真实。

图17：500小时内的真实(顶部)和生成(底部)序列。 该模型是无条件运行的。 我们可以看到，综合数据很好地捕获了每日和每周的模式。

为了测试所生成数据的质量，我们提供一些指标—参见表2：

· 相似度-通过直方图和相互信息的重叠来衡量

· 自相关-超过30个时滞的实数与合成数之比

· 效果—用实数和合成数据训练时，通过预测误差的相对比率来衡量

我们使用带有自举的LSTM(长期短期记忆)模型作为基准。 该LSTM模型由两层组成，每层包含100个神经元，并使用30小时的滑动窗口。 这些属性是通过密集层添加的，并连接到网络的最后一个隐藏层。

从表2中可以看出，经过每周数据训练的DoppelGANger的性能相对较好，在引导技术方面表现出色。

表2：流量数据集的结果

我们添加了第三个指标，即顺序相互信息(SMI)。 它正在评估包含T列的矩阵上的互信息，其中每列对应于之前的t，t-1，t-2，…t-T时间步长发生的事件，并平均属性子集。

我们应该注意，该模型可以以属性为条件，因此我们可以针对特定的天气条件或一周中的某天或某个月的某天生成样本。

差异隐私实验

在最初的工作中，作者通过众所周知的向鉴别器添加噪声并削减其梯度的技术(DPGAN)在模型中引入了差异隐私。

但是，他们发现，一旦隐私预算ε变得相对较小(意味着合成数据变得更安全，它也会开始失去质量)(通过相对于真实数据的时间一致性来衡量)。如果数据的最终用途是提取详细的时间信息，例如事件之间的因果关系，则这可能是一个主要问题。

基于有关PPGAN(隐私保护的生成对抗网络)的最新工作，我们对注入到鉴别器梯度的噪声进行了一些修改。瞬间的会计将隐私丢失问题视为一个随机变量，使用其瞬间生成函数来控制变量的密度分布。此属性使PPGAN模型训练更加稳定。当生成非常长的序列时，与DPGAN的区别特别明显。

噪声由以下表达式给出：

ɸ= f + N(0，σ2f2)

其中是两个相邻点x和x'对查询f的敏感度：

△f = maxf(x)-f(x')2

该表达式表示，大多数信息点(最高灵敏度)将获得更多的噪声添加到渐变，因此不会影响其他点的质量。通过使用经过精心设计的噪声，我们能够在交通数据上保留88％的自相关，直到ε= 1。

结论

合成顺序数据生成是一个尚未完全解决的难题。 通过上面介绍的测试，我们证明了GAN是解决此问题的有效方法。

本文源代码：github/fjxmlzn/DoppelGANger

作者:Armando Vieira

deephub翻译组