【论文笔记】基于生成对抗网络的强化学习算法的研究

摘要

• 解决：强化学习在训练样本中出现的整体工作效率滞后问题
• 提出：基于生成对抗网络的强化学习算法
• 主要内容：将真实经验样本集作为模板，生成理论上可行的虚拟样本，通过智能体agent进行一次训练，智能体agent会将好的虚拟样本并入到真实样本集当中，提高训练样本的质量
• 结果：对比Q学习算法，其输出的目标函数收敛次数大约少于40次

关键词

• 强化学习；
• 生成对抗网络；
• 训练样本；
• 相对熵；
• 函数收敛

0 引言

生成对抗网络是最近提出的一类生成模型，其训练了生成器以优化区分器同时学习的成本函数。

学者	工作	优缺点	引用文献
汪，焦等。	ASE学习算法，改进样本的采样工序来提高目标函数的精确度。	数据学习过程和应用能力方法没有提及，无法获取数据训练或者计算的过程，工作效率滞后，也无法解决相关技术问题。	汪悦颀，焦在滨．基于继电保护同步时序信息特征的配电网故障诊断方法[J]. 南方电网技术，2019，13（4）：73-79.
王，傅等。	通过小计算获取大效果的Q学习算法，计算量比较小，该算法能够输出较佳的数据最优解，对于解决复杂数据问题具有突出的技术效果，能够通过随机的方式实现数据的动态变化，大大提高了数据应用能力。	训练样本的过程复杂，且对计算机系统性能要求过高	王改花，傅钢善. 网络学习行为与成绩的预测及学习干预模型的设计[J]. 中国远程教育，2019（2）：39-48.

1 相关理论

1.1 强化学习理论

1.2 生成对抗网络理论

生成对抗网络作为生成建模的一种方法，通过生成模型G和判别模型D两种不同的方式实现数据信息评估与分析。

实现数据信息生成对抗网络的判别模型能够将数据信息通过输入分类数据信息，进而将数据信息通过生成模型的方式进行输出，进一步将能够实现的基础数据样本信息通过信息$p(x)$的形式实现输出。

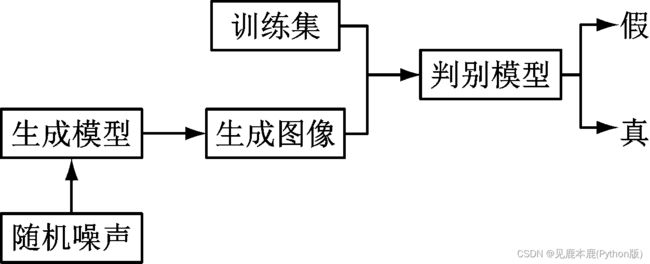
生成对抗网络模型的过程中，通常将对抗过程划分为极小、极大二元博 弈问题。

1. 将输出的噪声作为输入信息，并将输入的数据信息转化为样本数据集合$x-G$；
2. 通过判别模型也能够输出数据信息，并将数据样本数据信息集合记作为样本$x$，然后将样本数据集合$x$进行数据输入，其中输出样本数据信息通过分布式概率$D(x)$进行计算。
3. 通过判别模型输出的数据信息损失能够实现正确的信息分类，并通过平均对数概率实现网络数据信息损耗计算。

$$\underset{G}{\min }\underset{D}{\max }V(D,G)=E[\mathbf{log}D(x)]+E[\mathbf{log}(1-D(G(z)))]$$

生成模型的优化方向是使$D(x)$增 大，$D(G(z))$减小。判别模型输出的真实样本通过大概率取样，进而能够将生成模型样本概率值尽可能小；而判别模型与其理念相反。

训练样本过程：

1. $$V=E[\mathbf{log}D(x)]+E[\mathbf{log}(1-D(x))]$$
2. 写成积分形式：$$V={\int }_x[\mathbf{log}D(x)+\mathbf{log}(1-D(x))]\mathbf{d}x$$
3. 令：$\frac{\mathbf{d}V(G,D)}{\mathbf{d}D}=0$，得到：$$D(x)=\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$$其中$P_{data}$表示整个对抗模型训练出数据样本的概率，$P_G(x)$表示生成模型Ｇ训练出数据样本的概率。
4. 回代得到：$$V=-2\mathbf{log}2+2\mathbf{JSD}(P_{data}(x)|P_G(x))$$其中$\mathbf{JSD}$表示分布相似性的离散度。
5. 生成模型G训练出来的样本为：
   $$G=\underset{G}{\mathrm{argmin}}V(G,D)=\underset{G}{\mathrm{argmin}}[-2\mathbf{log}2+2\mathbf{JSD}(P_{data}(x)|P_G(x))]$$

判别模型的优先优化更有利于目标函数快速收敛，对训练样本的速度影响更大。

1.3 基于生成对抗网络的强化学习算法

1.3.1 算法总体结构框架

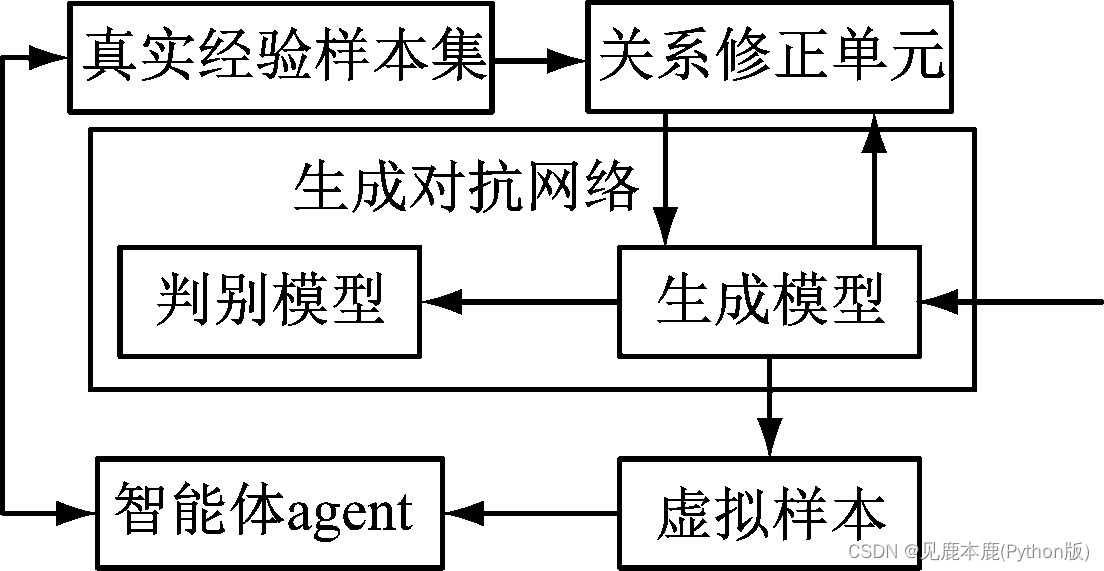
在训练初始情况下，将生成对抗网络算法模型的数学模型以及样本数据模型作为试验样本数据信息进行训练、分析，以生成新的样本，这种样本数据信息并不是历史数据所得出的真实经验，仅是理论上可行的数据样本，可称为虚拟样本。

真实经验样本集$C$和奖赏函数$r$表示如下：
$$C=[(s,a),(s^{\prime },r)]=[x_1,x_2]$$
通常通过生成有限的状态函数$s^{\prime }$实现数据信息的分析与计算

$$\begin{gathered} \mathbf{I}(x_1,x_2)=\mathbf{H}(x_2)-\mathbf{H}(x_2|x_1) \\ =P(x_2){\mathbf{log}}_{2}P(x_2)+P(x_2,x_1){\mathbf{log}}_{2}P(x_2|x_1) \\ =P(x_2,x_1){\mathbf{log}}_2(\frac{P(x_2,x_1)}{P(x_2)P(x_1)}) \end{gathered}$$

通过生成对抗网络算法模型生成经验样本集Ｇ:
$$C=[(s,a),(s^{\prime },r)]=[G_1,G_2]$$

引入相对熵（$KL$）的概念，用其表示$G_1$、$G_2$两者相似性。
$$D_{KL}(P||Q)=\sum _{i}p(i)\mathbf{log}\frac{p(i)}{q(i)}$$

2 实验与分析

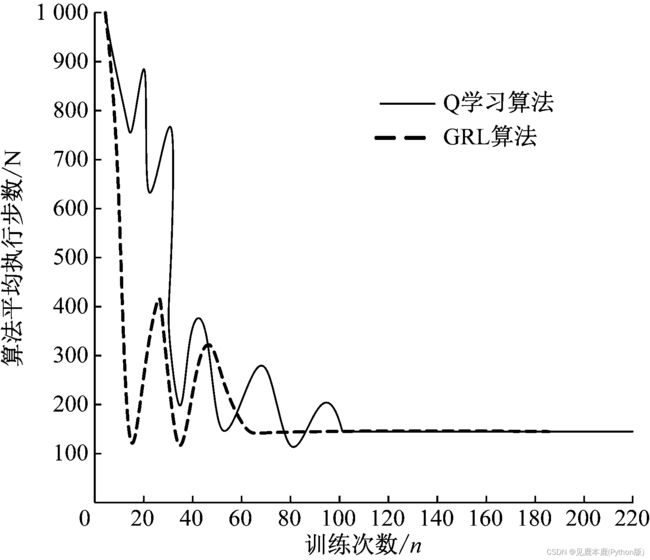
分析其原因在于采用生成对抗网络将真实经验样本集 $C$ 作为模板，生成新的虚拟样本并入到样本集 $C$ 当中，越早的加入生成新的虚拟样本，更新动作ａ的频率也就越大，因此在起始训练样本次数越低的情况下，用生成对抗网络的强化学习算法的系统性也就会更好，训练样本的速度也更快。

3 总结