一篇文章带你入门Pytorch

• 本教程假设你有一些神经网络的基础基础知识

---

0.安装Pytorch

• 1.我们可以从官网安装点击出发
• 2.我们也可以从镜像站安装，通过 pip install --upgrade torch torchvision -i https://pypi.tuna.tsinghua.edu.cn/simple

1.简单介绍Pytorch

pytorch是一个神经网络框架，可以快速的帮助我们搭建神经网络

2.Pytorch和Numpy

• pytorch和numpy几乎有差不多的功能

在numpy的我们的数据结构就是一个高维数组ndarray
在我们的Pytorch中，相当于numpy中ndarray的数据结构就是我们的Tensor。下面先了解一下Pytorch的基本用法吧！

# 引入torch模块(这就是我们的pytorch)        
import torch   
import numpy    
# 创建一个Tensor
torch_data = torch.Tensor([1,2,3]) 
# Torch ---> array 
np_data = torch_data.numpy()
# array ---> Torch
torch_data = torch.from_numpy(np_array)
# 求绝对值
torch.abs(torch_data)
# 创建一个全为1的矩阵
torch.ones((2,2)) 

• Pytorch的部分语法，都是和numpy相同的

3 激活函数

• 没有激活函数，我们的神经网络就永远只能处理线性问题，对于非线性问题，我们需要激活函数，来让我们的神经网络更好的处理非线性问题。
• 从torch.nn.function中引用
  很多的激活函数都可以从中引用，但有也有一小部分常用的需要我们从torch中引用

import torch.nn.functional as F 
import torch
# 引用方法
torch.rule()  # 这个必须要在torch中引用

F.sigmoid()
F.tanh()
F.softplus()

• 下面是几个激活函数的图片
  

4.误差反向传播

• 误差反向传播，是神经网络中的一个重要的功能，让我们不断更新我们神经元的权重，从而使我们的神经网络不断优化

import torch
from torch.autograd import Variable

x = torch.Tensor([[1,2],[3,4]])
# 开启反向传播的功能
x.requires_grad=True

y = torch.mean(x*x)  # v^2
# 进行误差反向传播
y.backward()
# 查看误差
print(x.grad)   

5.搭建一个简单的神经网络

# 导入我们需要的模块
import torch
import torch.nn.functional as F
import numpy as np

• 定义我们的神经网络

# 定义神经网络
class Net(torch.nn.Module):
	# n_feature 输入的神经元的数目  n_hidden 隐藏层中的神经元数目 n_output输入神经元的数目
    def __init__(self,n_feature,n_hidden,n_output,):
        super(Net,self).__init__()  # 必要步骤 调用父类
        # 定义我们的隐藏层
        self.hidden = torch.nn.Linear(n_feature,n_hidden)
        # 定义我们的输入层
        self.predict = torch.nn.Linear(n_hidden,n_output)
        
    def forward(self,x):
   		# 在我们的隐藏层，和输入层之间 加上我们的激活函数
        x = F.relu(self.hidden(x))
        x = self.predict(x)
        return x
       	
# 一个输入神经元   10个隐藏神经元 1个输出神经元
net = Net(1,10,1)
# 打印这个神经网络
print(net)

---

Out
Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)

• 快速定义我们的神经网络的方法

net2 = torch.nn.Sequential(
        torch.nn.Linear(1,10),
        torch.nn.ReLU(),
        torch.nn.Linear(10,1)
)
print(net2) # 和第一个的结果是一样的

---

6.优化器与误差函数

• 损失函数 （通过计算损失，来让我们优化我们的神经网络）
• 下面是均方误差来当我们的误差函数

loss_func = torch.nn.MSELoss()
# 对于分类的任务  使用交叉熵作为误差函数会更好一些
loss_func = CrossEntropyLoss()

• 优化器能让我们更快的更好的优化我们的神经网络
• 不同的优化器，将会有不同的效果

# 随机梯度下降的优化器
# Net是我们上节的神经网络 # Net.parameters() 是我们的神经网络的参数
net_SGD = Net() 
# 里面的的参数是： 我们神经网络的参数，和学习率，学习率，是我们更新参数的幅度
torch.optim.SGD(net_SGD.parameters(),lr=0.01) 

	学习率 大	学习率小
收敛速度	收敛速度快	收敛速度慢
缺点	容易在最优点震荡	容易过拟合

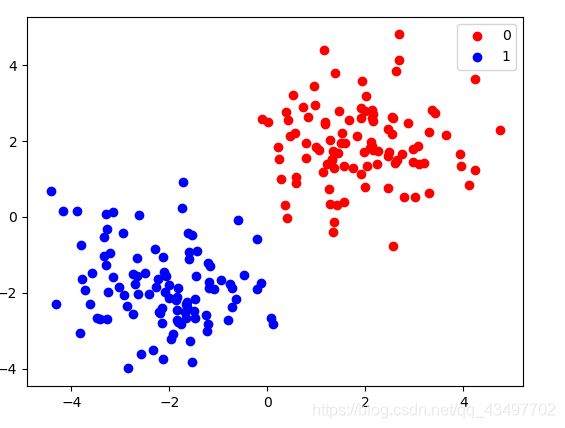
7.实战一个简单的分类任务

import torch 
import torch.nn.functional as F
import numpy as np

######创建一个假数据######
n_data = torch.ones(100,2)
# 第一个数据集
x0 = torch.normal(2*n_data,1)
y0 = torch.zeros(100)
# 第二个数据集
x1 = torch.normal(-2*n_data,1)
y1 = torch.ones(100)
# 合并数据集  --> 合并 并改变格式
x = torch.cat((x0,x1),0).type(torch.FloatTensor)     # 32位浮点数
y = torch.cat((y0,y1)).type(torch.LongTensor)         # 64 位整型

• 查看我们的数据
• 这个数据是只有两个特征的(x,y)
• 标签是0或1,红色的数据是第一个数据集，蓝色的数据是第二个数据集的。
  

######定义我们的神经网络#######
class Net(torch.nn.Module):
	# n_feature 输入的神经元的数目  n_hidden 隐藏层中的神经元数目 n_output输入神经元的数目
    def __init__(self,n_feature,n_hidden,n_output):
    	# 必要步骤 调用父类
        super(Net,self).__init__()
        self.hidden = torch.nn.Linear(n_feature,n_hidden)
        self.predict = torch.nn.Linear(n_hidden,n_output)
    def forward(self,x):
        x = F.relu(self.hidden(x))
        x =self.predict(x)
        return x
######实例化我们的神经网络######
net = Net(2,10,2)
optimizer = torch.optim.SGD(net.parameters(),lr=0.1)
loss_func = torch.nn.CrossEntropyLoss()      # 使用标签误差
######训练我们的神经网络######
for i in range(100):
    prediction = net(x)
    loss = loss_func(prediction,y)
    # 梯度归零
    optimizer.zero_grad()
    # 计算梯度
    loss.backward()
    # 更新结点
    optimizer.step()
    if i % 20 == 0:
        print(loss)

---

Out
tensor(0.5676, grad_fn=)
tensor(0.0800, grad_fn=)
tensor(0.0339, grad_fn=)
tensor(0.0204, grad_fn=)
tensor(0.0143, grad_fn=)

---

######作出预测######
x1 = torch.FloatTensor([2,2])  # !!! 必须要转换成Tensor的形式
np.argmax(net(x1).data.numpy)

######保存我们的神经网络######
#保留全部的神经网络
torch.save(net1 ,'net.pkl')
#只保留神经网络的参数
torch.save(net1.state_dict(), 'net_params.pkl' )
# 提取神经网络
net2 = torch.load('.//pkl//net.pkl')
# 用参数还原神经网络 ！！首先我们必须创造一个和原来具有一样结构的神经网络
net3 = torch.nn.Sequential(
torch.nn.Linear(2,10),
torch.nn.ReLu(),
torch.nn.Linear(10,2)
)
net3.load_state_dict(torch.load('.//pkl/net_params'))

Congratulations！ 你已经成功的开启了你的Pytorch的第一步！