LeetCode题解 - 深度优先搜索

深度优先搜索

广度优先搜索一层一层遍历，每一层得到的所有新节点，要用队列存储起来以备下一层遍历的时候再遍历。

而深度优先搜索在得到一个新节点时立即对新节点进行遍历：从节点 0 出发开始遍历，得到到新节点 6 时，立马对新节点 6 进行遍历，得到新节点 4；如此反复以这种方式遍历新节点，直到没有新节点了，此时返回。返回到根节点 0 的情况是，继续对根节点 0 进行遍历，得到新节点 2，然后继续以上步骤。

从一个节点出发，使用 DFS 对一个图进行遍历时，能够遍历到的节点都是从初始节点可达的，DFS 常用来求解这种 可达性 问题。

在程序实现 DFS 时需要考虑以下问题：

• 栈：用栈来保存当前节点信息，当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
• 标记：和 BFS 一样同样需要对已经遍历过的节点进行标记。

---

547. 省份数量（中等）

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

解题思路：可以把 n 个城市和它们之间的相连关系看成图，城市是图中的节点，相连关系是图中的边，给定的矩阵 isConnected 即为图的邻接矩阵，省份即为图中的连通分量。

计算省份总数，等价于计算图中的连通分量数，可以通过深度优先搜索或广度优先搜索实现，也可以通过并查集实现。

深度优先搜索的思路是很直观的，即图的遍历。遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 isConnected 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。遍历完全部城市以后，即可得到连通分量的总数，即省份的总数。

class Solution {
    public int findCircleNum(int[][] isConnected) {
        if(isConnected == null || isConnected.length == 0){
            return 0;
        }
        int n = isConnected.length;
        boolean[] visited = new boolean[n];// 定义 boolean 数组标识顶点是否被访问
        int circle = 0;// 定义 circle 来累计遍历过的连通域的数量
        for(int i = 0; i < n; i++){
            // 若当前顶点 i 未被访问，说明又是一个新的连通域，则遍历新的连通域且circle+=1.
            if( !visited[i]){
                dfs(isConnected, i, visited);
                circle ++;
            }               
        }
        return circle;
    }
        

    private void dfs(int[][] isConnected, int i, boolean[] visited){
        int n = isConnected.length;
        // 对当前顶点 i 进行访问标记
        visited[i] = true;
        for(int j = 0; j < n; j ++){
            // 继续遍历与顶点 i 相邻的顶点（使用 visited 数组防止重复访问）
            if(isConnected[i][j] == 1 && !visited[j]){
                dfs(isConnected, j, visited);
            }          
        }
    }
}

---

网格类问题的 DFS 遍历方法

参考链接

我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题，是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些，如果没有掌握一定的方法，DFS 代码容易写得冗长繁杂。

本文将以岛屿问题为例，展示网格类问题 DFS 通用思路，以及如何让代码变得简洁。

1. 网格问题的基本概念

我们首先明确一下岛屿问题中的网格结构是如何定义的，网格问题是由 m×n 个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。

岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子，数字为 1 的格子看成陆地格子，这样相邻的陆地格子就连接成一个岛屿。

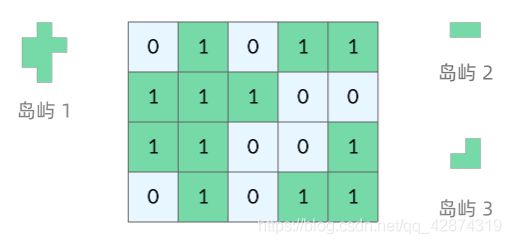
在这样一个设定下，就出现了各种岛屿问题的变种，包括岛屿的数量、面积、周长等。不过这些问题，基本都可以用 DFS 遍历来解决。

2. DFS 的基本结构

网格结构要比二叉树结构稍微复杂一些，它其实是一种简化版的图结构。要写好网格上的 DFS 遍历，我们首先要理解二叉树上的 DFS 遍历方法，再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的：

void traverse(TreeNode root) {
    // 判断 base case
    if (root == null) {
        return;
    }
    // 访问两个相邻结点：左子结点、右子结点
    traverse(root.left);
    traverse(root.right);
}

可以看到，二叉树的 DFS 有两个要素：「访问相邻结点」和「判断 base case」。

第一个要素是访问相邻结点。二叉树的相邻结点非常简单，只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构：一棵二叉树，它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。

第二个要素是 判断 base case。一般来说，二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义：一方面，这表示 root 指向的子树为空，不需要再往下遍历了。另一方面，在 root == null 的时候及时返回，可以让后面的 root.left 和 root.right 操作不会出现空指针异常。

对于网格上的 DFS，我们完全可以参考二叉树的 DFS，写出网格 DFS 的两个要素：

首先，网格结构中的格子有多少相邻结点？答案是上下左右四个。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说，网格结构是「四叉」的。

其次，网格 DFS 中的 base case 是什么？从二叉树的 base case 对应过来，应该是网格中不需要继续遍历、grid[r][c]会出现数组下标越界异常的格子，也就是那些超出网格范围的格子。

这样，我们得到了网格 DFS 遍历的框架代码：

void dfs(int[][] grid, int r, int c) {
    // 判断 base case
    // 如果坐标 (r, c) 超出了网格范围，直接返回
    if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length ) {
        return;
    }
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

3. 如何避免重复遍历

网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。这是因为，网格结构本质上是一个「图」，我们可以把每个格子看成图中的结点，每个结点有向上下左右的四条边。在图中遍历时，自然可能遇到重复遍历结点。

如何避免这样的重复遍历呢？答案是标记已经遍历过的格子。以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值置0，这样当我们遇到 0 的时候直接跳过即可：

void dfs(int[][] grid, int r, int c) {
    // 判断 base case
    if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length ) {
        return;
    }
    // 如果这个格子不是岛屿，直接返回
    if (grid[r][c] == 0) {
        return;
    }
    grid[r][c] = 0; // 将格子标记为「已遍历过」
    
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

这样，我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法。以下所讲的几个例题，其实都只需要在 DFS 遍历框架上稍加修改而已。

小贴士：把「已遍历过的陆地格子」标记为和海洋格子一样的 0，名曰「陆地沉没方法」，即遍历完一个陆地格子就让陆地「沉没」为海洋。这种方法看似很巧妙，但实际上有很大隐患，因为这样我们就无法区分「海洋格子」和「已遍历过的陆地格子」了。如果题目更复杂一点，我们可以每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了，0则为海洋格子

---

463. 岛屿的周长（简单）

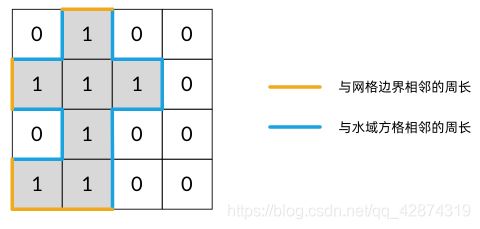
给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

解题思路：求岛屿的周长其实有很多种方法，如果用 DFS 遍历来求的话，有一种很简单的思路：对于一个陆地格子的每条边，它被算作岛屿的周长当且仅当这条边为网格的边界或者相邻的另一个格子为水域。 因此，我们可以遍历每个陆地格子，看其四个方向是否为边界或者水域，如果是，将这条边的贡献（即 1）加入答案 ans 中即可。我们可以画一张图，看得更清晰：

class Solution {
    int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    public int islandPerimeter(int[][] grid) {
        if(grid == null || grid.length == 0) return 0;
        int m = grid.length, n = grid[0].length;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j ++){
                if(grid[i][j] == 1){
                    return dfs(grid, i, j);// 题目限制只有一个岛屿，计算一个即可，如果是多个则需要计算累加和
                }
            }
        }
        return 0;
    }

    private int dfs(int[][] grid, int row, int col){
        int m = grid.length, n = grid[0].length;
        //如果是边界或者是水域，则返回周长1
        if(row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == 0){
            return 1;
        }
        if(grid[row][col] == 2){//如果之前遍历过则返回0
            return 0;
        }
        grid[row][col] = 2;//已经遍历过的方格置为2
        int perimeter = 0;
        for(int[] dir : directions){
            perimeter += dfs(grid, row + dir[0], col + dir[1]);
        }
        return perimeter;
    }
}

---

695. 岛屿的最大面积（中等）

给定一个包含了一些 0 和 1 的非空二维数组 grid 。一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。

输入：[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1

解题思路：要确定岛屿的最大面积，首先遍历二维数组中的每一个值，如果是0就跳过，如果是1就采用深度优先搜索方法，将此位置向四周扩散的节点都设为0，同时为这些为1的节点计数，直到所有的点都遍历结束，取出最大的面积即可。

class Solution {
    int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    int maxArea = 0;
    public int maxAreaOfIsland(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        int m = grid.length, n = grid[0].length;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){              
                maxArea = Math.max(maxArea, dfs(grid, i, j));//遍历 所有区域，将每一块区域进行计算 “相连陆地大小”并求出最大值
            }
        }
        return maxArea;
    }

    private int dfs(int[][] grid, int row, int col){
        int m = grid.length, n = grid[0].length;
        if(row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == 0){
            return 0;//深度优先遍历：直到到达边界条件或者不满足条件则返回
        }
		// 剪枝：将 当前这块区域 置为 水（避免之后搜索时重复计算同一块区域）
        grid[row][col] = 0;
        int area = 1;//当前岛屿初始面积为1
        for(int[] dir : directions){
            area += dfs(grid, row + dir[0], col + dir[1]);
        }
        return area;
    }  
}

---

200. 岛屿数量（中等）

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围。

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

解题思路：我们可以将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边相连。

为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 1，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0。最终岛屿的数量就是我们进行深度优先搜索的次数。

class Solution {
    int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    public int numIslands(char[][] grid) {
        if(grid == null || grid.length == 0){
            return 0;
        }
        int m = grid.length, n = grid[0].length;
        int IslandsNum = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] != '0'){
                    dfs(grid, i, j);
                    IslandsNum ++;
                }
            }
        }
        return IslandsNum;
    }

    private void dfs(char[][] grid, int row, int col){
        int m = grid.length, n = grid[0].length;
        if(row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == '0'){
            return;
        }
        grid[row][col] = '0';
        for(int[] dir : directions){
            dfs(grid, row + dir[0], col + dir[1]);
        }
    }
}

---

130. 被围绕的区域（中等）

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

注意：与边界连通的‘O’不需要被填充

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

解题思路：注意到题目解释中提到：任何边界上的 O 都不会被填充为 X。 所以我们会想到边界上的 O 要特殊处理，只要把边界上的 O 特殊处理了，那么剩下的 O 替换成 X 就可以了。问题转化为，如何寻找和边界联通的 O。

我们需要考虑如下情况。

X X X X
X O O X
X X O X
X O O X

这时候的 O 是不做替换的。因为和边界是连通的。为了记录这种状态，我们把这种情况下的 O 换成 T 作为占位符，待搜索结束之后，遇到 O 替换为 X（和边界不连通的 O）；遇到 T ，替换回 O(和边界连通的 O)。

如何寻找和边界联通的O? 从边界出发，对图进行 dfs即可。

class Solution {
    int[][] directions = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
    public void solve(char[][] board) {
        if(board == null || board.length == 0) return;
        int m = board.length, n = board[0].length;
        //从边界上的每一点出发，进行深度优先搜索，找到与边界连通的O
        for(int i = 0; i < m; i++){
            dfs(board, i, 0);
            dfs(board, i, n - 1);
        }
        for(int j = 0; j < n; j++){
            dfs(board, 0, j);
            dfs(board, m - 1, j);
        }
		//遍历整个矩阵，若遇到T则还原为O,若遇到O,则将他填充为X
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(board[i][j] == 'T'){
                    board[i][j] = 'O';
                }else if(board[i][j] == 'O'){
                    board[i][j] = 'X';
                }
            }
        }
    }

    private void dfs(char[][] board, int row, int col){
        int m = board.length, n = board[0].length;
        if(row < 0 || row >= m  || col < 0 || col >= n || board[row][col] != 'O'){
            return;
        }
	//将与边界连通的O替换为T
        board[row][col] = 'T';
        for(int[] dir : directions){
            dfs(board, row + dir[0], col + dir[1]);
        }
    }
}

---

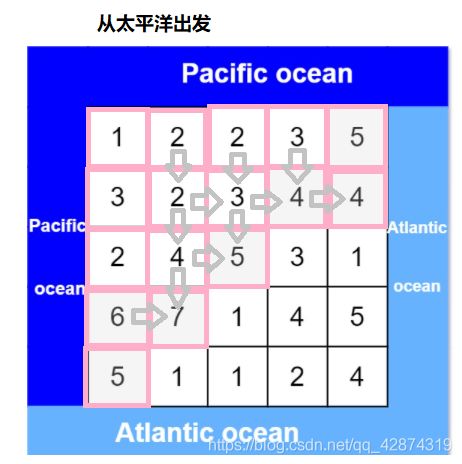
417. 太平洋大西洋水流问题（中等）

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

给定下面的 5x5 矩阵:

  太平洋 ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).

解题思路：对于一个点它能流动两边的大洋，那么反过来，两边大洋的水反着流就能达到这个点，那么与上题思路类似，我们从四个边界的点开始进行深度优先搜索。既然水开始倒流了，那么逻辑也需要反过来，因此只有将下一个点比当前的点大时或者等于当前点的高度时，水才能流过去。

找出所有这样的点我们需要怎么做？

1. 找出所有从太平洋出发的水所能达到的点
   

2. 找出所有从大西洋出发的水所能达到的点
   

3. 这些重合的点便是我们要找的点
   

class Solution {
    int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        if(heights == null || heights.length == 0) return res;
        int m = heights.length, n = heights[0].length;
        boolean[][] reachT = new boolean[m][n];
        boolean[][] reachW = new boolean[m][n];
        //从四个边界的点开始进行dfs，找到它们能够到达的点
        for(int i = 0; i < m; i++){
            dfs(heights, i, 0, reachW);
            dfs(heights, i, n - 1, reachT);
        }
        for(int j = 0; j < n; j++){
            dfs(heights, 0, j, reachW);
            dfs(heights, m - 1, j, reachT);
        }

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                //取两个集合的交集即为可以互相流动的位置
                if(reachT[i][j] && reachW[i][j]){
                    res.add(Arrays.asList(i, j));
                }
            }
        }
        return res;
    }

    private void dfs(int[][] heights, int i, int j, boolean[][] reach){
        int m = heights.length, n = heights[0].length;
        if(reach[i][j]) return;
        reach[i][j] = true;
        for(int[] dir : directions){
            int row = i + dir[0], col = j + dir[1];
            if(row < 0 || row >= m || col < 0 || col >= n || heights[row][col] < heights[i][j]){
                continue;
            }
            dfs(heights, row, col, reach);
        }
    }
    //或者以下方式
    //private void dfs(int[][] heights, int i, int j, boolean[][] reach){
        //int m = heights.length, n = heights[0].length;
        //reach[i][j] = true;
        //for(int[] dir : directions){
            //int row = i + dir[0], col = j + dir[1];
            //if(row >= 0 && row < m && col >= 0 && col < n && !reach[row][col]){
               // if(heights[row][col] >= heights[i][j]){
               //    dfs(heights, row, col, reach);
               // }  
           // }               
       // }
   // }
}