基于形态学的目标检测——统计大米数量

记录一下MATLAB期末考试大作业，因为学校提前放假，期末考试延迟到下学期 (ノへ￣、)
不对！我还没开始复习！我差点没时间复习！ヾ(≧▽≦*)o
MATLAB线下考试也改为了大作业，要求我们找一个Toolbox学习，最后自拟题目写个报告，思前想后，最终决定使用Image Processing Toolbox，一方面，我有一点点图像处理的基础，其次，我觉得这个方向在老师眼里会比较有前途（比较nb）
ok，废话不多说，下面就是肝了一个通宵的作业。

问题描述

这是MATLAB自带的大米图片（‘rice.png’） ，在Image Processing Toolbox的 入门实例 用到该图片，对图片进行预处理后，得到二值图，最后查找二值图中的所有连通分量，从而识别出所有大米。

而这是 @ctrlC&&ctrlV 拍的一张大米图片，与上面的图片相比，它的背景更加复杂，它的对象也更加复杂——大米不全是独立的、分离的，这意味着在一个连通分量内可能存在多个对象，直接统计所有分量将不再适用。

尝试识别并统计出第二张图片中所有大米的数量。

设计思路

可以看出，图片中间背景比周围更亮。为方便分析，需要对图像预处理，转化二值图像、去除背景噪声，此时，对连通分量做标签处理，最后对粘连的米粒对象做形态学上的处理，从而实现分离米粒的目的。

实现过程

• 载入图片

srcImage=imread('my_rice.jpg');
figure, imshow(srcImage), title('原始图片');

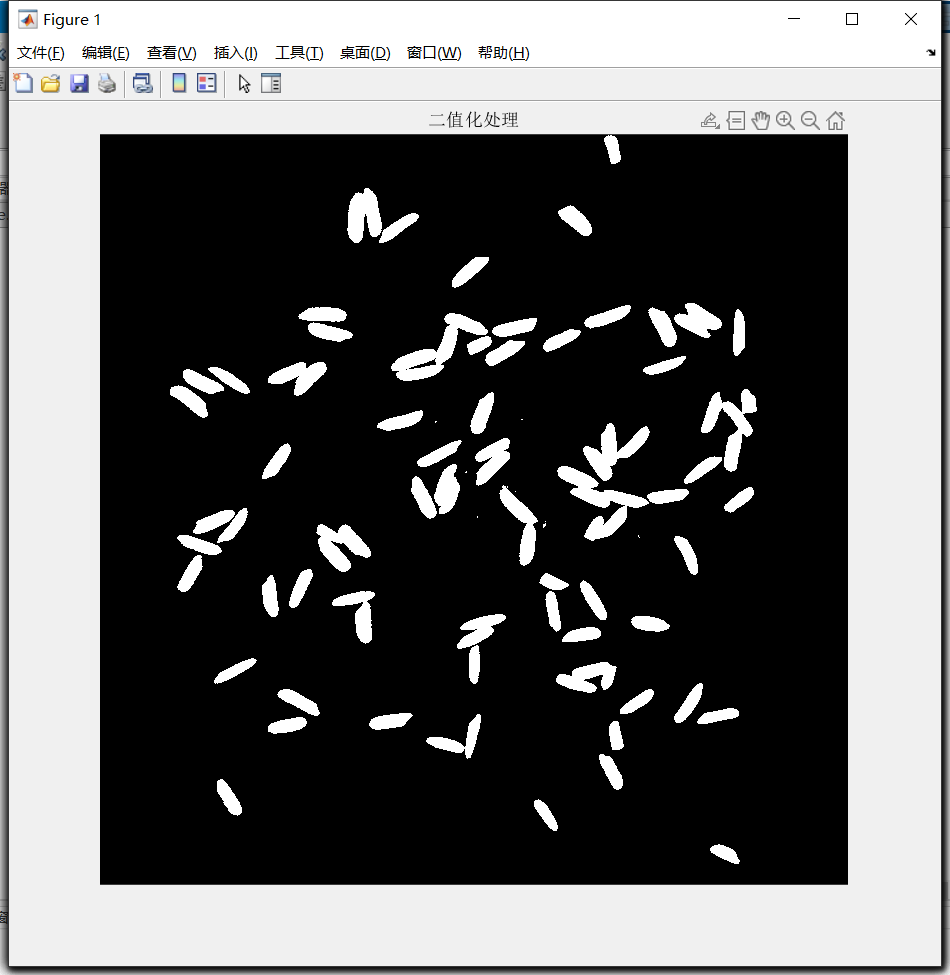
• 二值化处理

im = rgb2gray(srcImage);
bw = imbinarize(im, graythresh(im));
figure, imshow(bw), title('二值化处理');

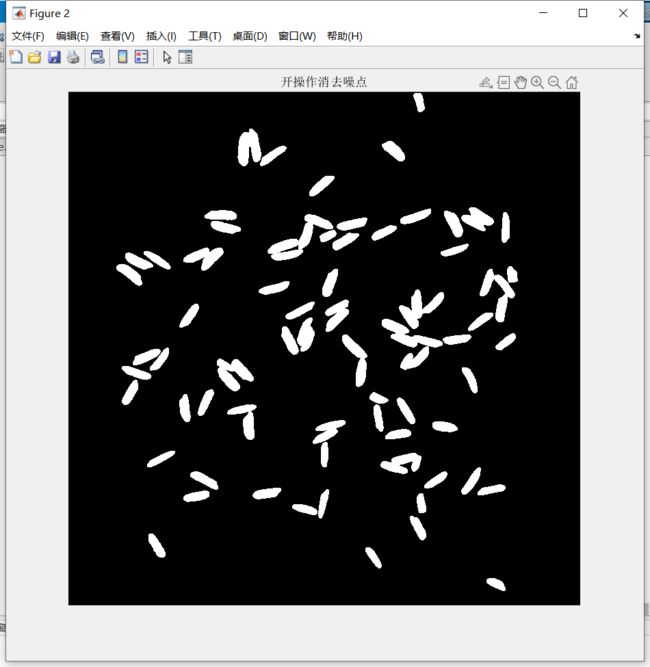
• 开操作去除噪点

se = strel('disk',10);
openbw = imopen(bw,se);
figure, imshow(openbw), title('开操作去除噪点');

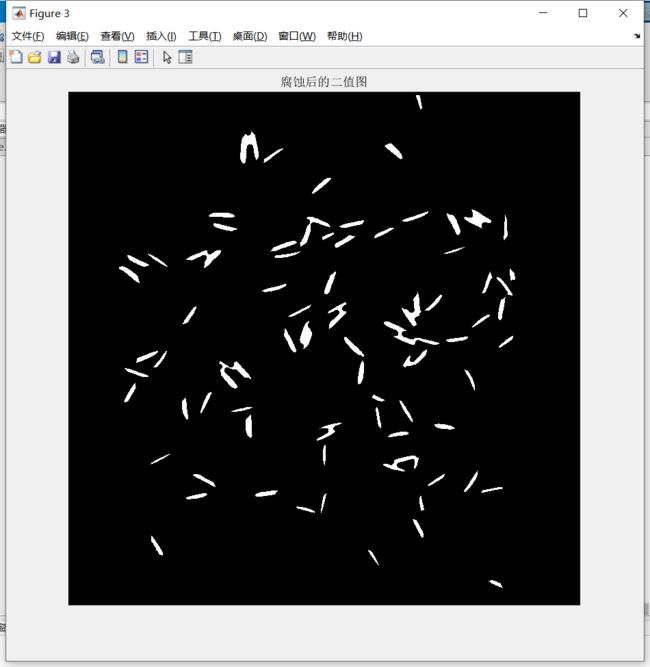
• 形态学处理，腐蚀图像

se = strel('disk',15);
openbw = imerode(openbw,se);  
figure, imshow(openbw), title('腐蚀后的二值图');

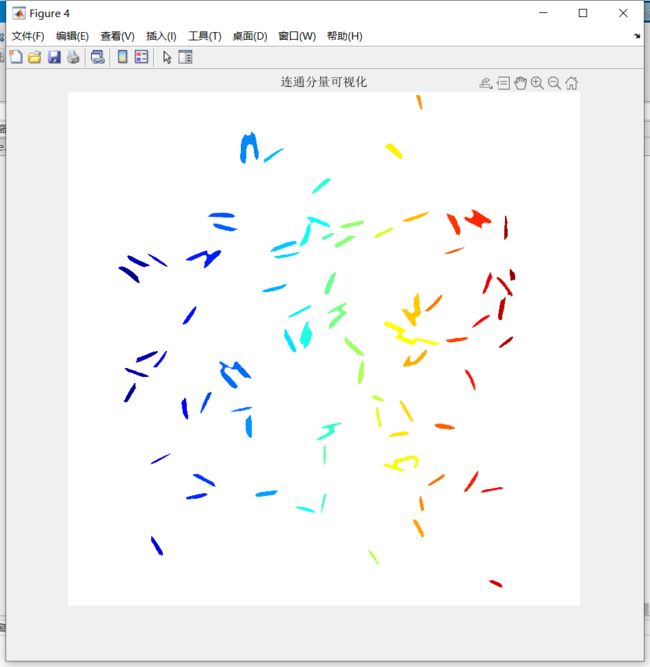
• 获取连通区域，并进行显示

L = bwlabel(openbw,8);
RGB = label2rgb(L);
figure, imshow(RGB), title('连通分量可视化');

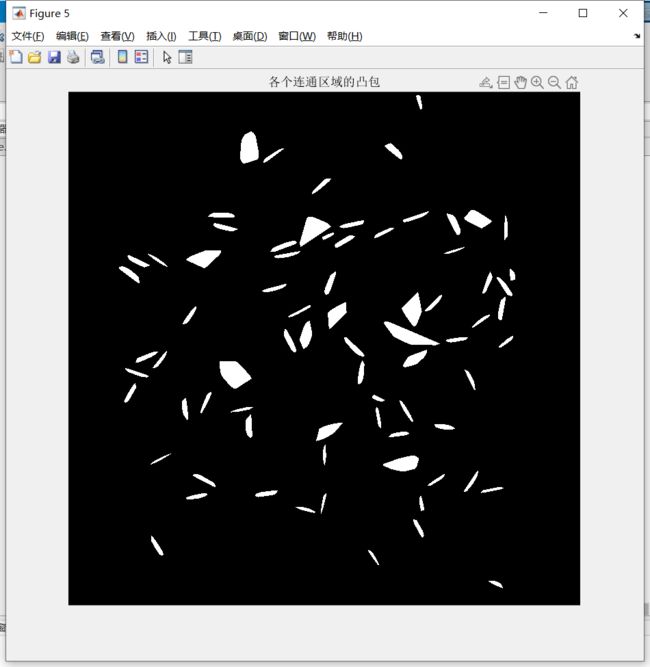
• 求各个连通区域的凸包

convex_img = zeros(size(im));
status = regionprops(L, 'ConvexHull');
for i = 1:size(status,1)
     tn = uint16(status(i).ConvexHull);
     convex_img = convex_img + roipoly(im,tn(:, 1),tn(:, 2));
end
figure, imshow(convex_img), title('各个连通区域的凸包');

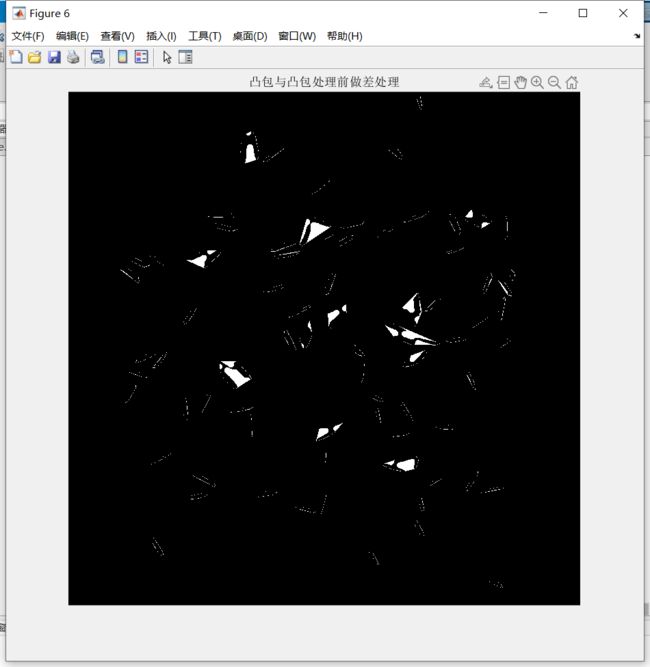
• 凸包与凸包处理前做差处理

diff_img = convex_img-openbw;
figure, imshow(diff_img), title('凸包与凸包处理前做差处理');   

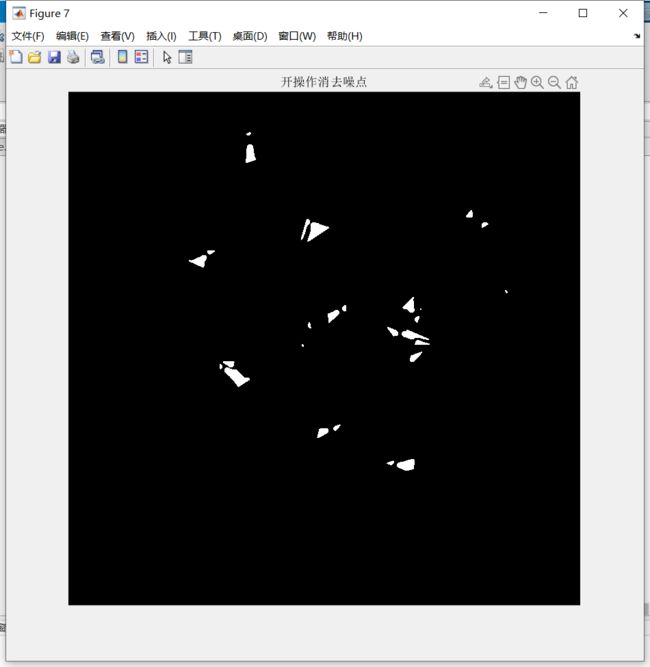
• 运用开操作消去噪点

se = strel('disk',5);
diff_open = imopen(diff_img,se); 
figure, imshow(diff_open), title('开操作消去噪点');

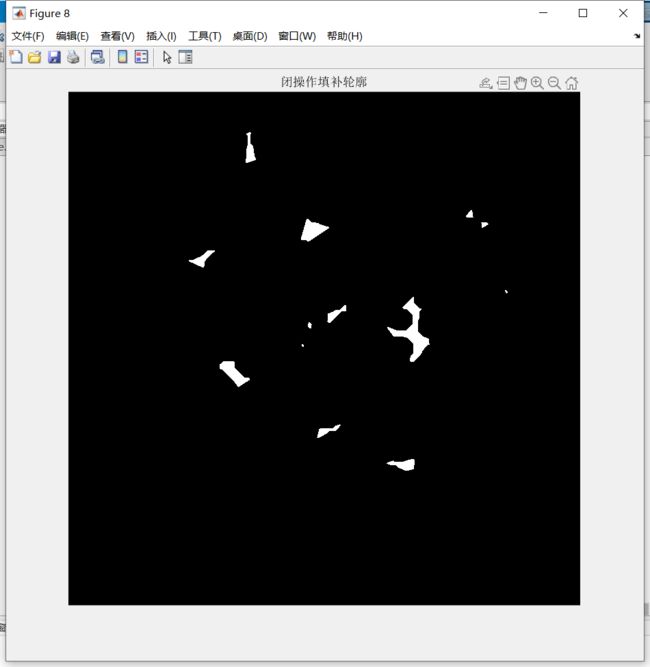
• 运用闭操作填补轮廓

se = strel('disk',60);
diff_close = imclose(diff_open,se); 
figure, imshow(diff_close), title('闭操作填补轮廓');

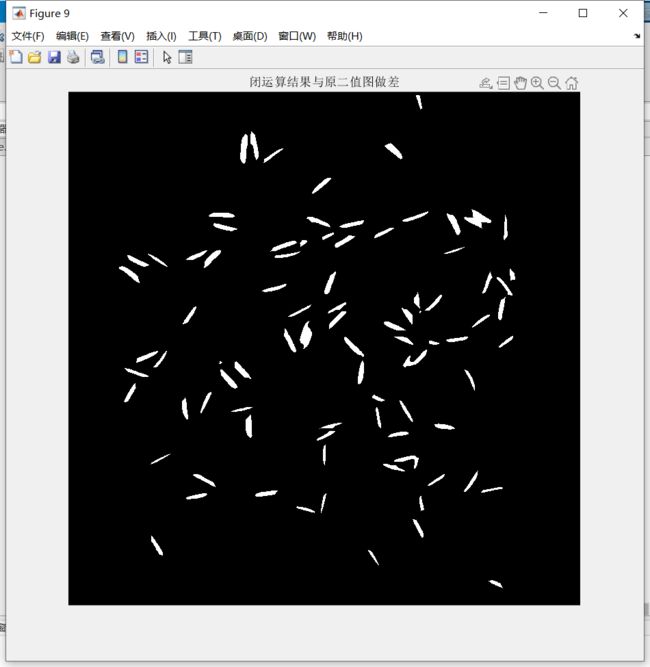
• 闭运算结果与原二值图做差

diff_img = openbw-diff_close;
figure, imshow(diff_img), title('闭运算结果与原二值图做差');

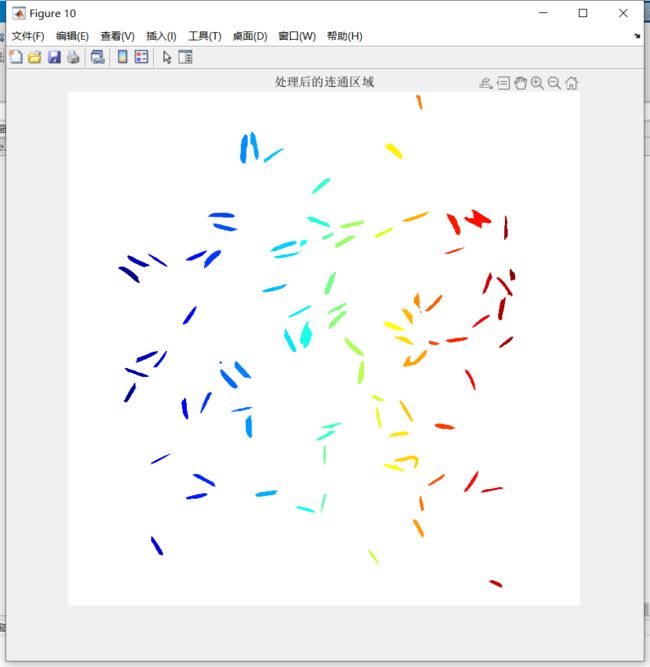
• 获取连通区域，并进行显示

diff_img = imbinarize(diff_img, graythresh(diff_img));
[L,num] = bwlabel(final_img, 8);
status = regionprops(L,'BoundingBox'); % 获取标记框
centroid = regionprops(L,'Centroid'); % 获取标记中心
RGB = label2rgb(L);
figure, imshow(RGB), title('处理后的连通区域');

• 最终显示结果

figure, imshow(srcImage), title(sprintf("大米数量为%d",num));
hold on;
for n = 1:num
	rectangle('position',status(n).BoundingBox,'edgecolor','r'); % 画框
    text(centroid(n,1).Centroid(1,1)-1,centroid(n,1).Centroid(1,2)-1, num2str(n),'Color', 'r')  % 标号
end

完整代码

clear, clc, close all

%载入图片
srcImage=imread('my_rice.jpg');

im = rgb2gray(srcImage);
bw = imbinarize(im, graythresh(im));

%运用开操作消去噪点
se = strel('disk',10);
openbw = imopen(bw,se);

% 形态学处理，腐蚀图像
se = strel('disk',15);
openbw = imerode(openbw,se);  

%获取连通区域，并进行显示
L = bwlabel(openbw,8);
RGB = label2rgb(L);

% 求各个连通区域的凸包
convex_img = zeros(size(im));
status = regionprops(L, 'ConvexHull');
for i = 1:size(status,1)
     tn = uint16(status(i).ConvexHull);
     convex_img = convex_img + roipoly(im,tn(:, 1),tn(:, 2));
end

% 凸包与凸包处理前做差处理
diff_img = convex_img-openbw;

% 运用开操作消去噪点
se = strel('disk',5);
diff_open = imopen(diff_img,se); 

% 运用闭操作填补轮廓
se = strel('disk',60);
diff_close = imclose(diff_open,se); 

% 闭运算结果与原二值图做差
diff_img = openbw-diff_close;

% 获取连通区域，并进行显示
diff_img = imbinarize(diff_img, graythresh(diff_img));
[L,num] = bwlabel(diff_img, 8);
status = regionprops(L,'BoundingBox'); % 获取标记框
centroid = regionprops(L,'Centroid'); % 获取标记中心
RGB = label2rgb(L);

% 最终显示结果
figure, imshow(srcImage), title(sprintf("大米数量为%d",num));
hold on;
for n = 1:num
	rectangle('position',status(n).BoundingBox,'edgecolor','r'); % 画框
    text(centroid(n,1).Centroid(1,1)-1,centroid(n,1).Centroid(1,2)-1, num2str(n),'Color', 'r')  % 标号
end

结论

通过对图像进行多次形态学处理后，成功识别出图像的米粒位置，除极少数难于分割外，基本完成了统计大米数量的问题。

在初次遇到这个问题时，就想着示例为什么不考虑目标对象粘连的情况，本以为只需做个简单的形态学处理，便能得到理想的结果，动手后方才发现，这比最初的设想难太多了。由于米粒的形状是细长条型，而且方向随机，无论是选用碟形还是矩形作为结构元，都难以通过腐蚀分离相邻的米粒，后来又尝试了分水岭算法，但由于目标太小以及粘连部分与米粒本身的高度差异不大，所以最终也没啥效果。最后决定，一层层突破，先分离已经独立的米粒，再逐步分割粘连的米粒，意外发现效果还不错，粘连的米粒大部分成功分割了。

基于传统图像处理的方法，在细小目标的图像分割上还是有不少短板的，或许可以通过深度学习的方法，实现更高效更准确的识别分割。