彻底搞懂交叉熵、信息熵、相对熵、KL散度、交叉熵损失函数

熵

什么是熵呢？

简单来讲，熵就是表示一个事件的确定性程度如何。

通常，一个信源发送出什么符号是不确定的，衡量它可以根据其出现的概率来度量。

比如假设事件Q，有A、B、C三种情况都是有概率性发生的，但是不定。如果其中A比B、C两种种发生的概率更大，那么事件Q发生A的可能性更加确定，换句话说，不确定性更小；如果其中A与B、C两种发生的概率都相等，那么事件Q发生A、B、C的情况都有可能，不确定会发生哪一个，换句话说，不确定性更大。

所以确定性程度越大（即不确定性程度越低），熵越小；确定性程度越低（即不确定性程度越高），熵越大。

信息熵

信息熵与熵含义相同，仅仅只不过是在不同领域叫的名称不同。

定义： 信息熵的计算公式如图所示：
$$H(x)=-\sum _{x\in X}p(x)lo{g}_{2}p(x)$$
不要问为什么这么写，目前我也没有了解，先记着。

注意： 在这里log并非一定是2为底，也可以是10、e，对结果没有任何影响，不需要纠缠。

相对熵与KL散度

首先你会在网上看到两种概念，一种是相对熵，一种是KL散度，这两种是一样的：

相对熵，又被称为Kullback-Leibler散度（KL散度）或信息散度，是两个概率分布间差异的非对称性度量。

• 相对熵就是KL散度，相对熵=KL散度
• KL散度就是相对熵，KL散度=相对熵

定义： KL散度计算公式如图所示：

离散形式：
$$KL(P||Q)=\sum P(x)log\frac{P(x)}{Q(x)}$$
连续形式：
$$KL(P||Q)=\int P(x)log\frac{P(x)}{Q(x)}dx$$
含义： KL散度是衡量两个概率分布间差异的非对称性度量标准。

通俗来讲，KL散度是用来衡量同一个随机变量的两个不同概率分布之间的距离。

比如：交叉熵就是表示一个随机变量的预测概率分布Q与真实概率分布P之间的差距。

特性：

• 非负性：由吉布斯不等式可知，KL散度恒大于等于0。

• 非对称性：相对熵是两个概率分布的不对称性度量，即：
  $$KL(P||Q)\ne KL(Q||P)$$
  假设P表示随机变量的真实分布，Q表示理论、预测或拟合分布。

  注意： 只有在P与Q概率分布一模一样的时候，前向KL散度才与后向KL散度相等。

在优化问题中，若P表示随机变量的真实分布，Q表示理论或拟合分布，则KL(P||Q)被称为前向KL散度,KL(Q||P)被称为后项KL散度。前向散度中拟合分布是KL散度公式的分母，因此若在随机变量的某个取值范围中，拟合分布的取值趋于0，则此时KL散度的取值趋于无穷。因此使用前向KL散度最小化拟合分布和真实分布的距离时，拟合分布趋向于覆盖理论分布的所有范围。前向KL散度的上述性质被称为“0避免”。相反地，当使用后向KL散度求解拟合分布时，由于拟合分布是分子，其0值不影响KL散度的积分，反而是有利的，因此后项KL散度是“0趋近”的 。

结论： 相对熵（KL散度）可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增大时，它们的相对熵也会增大。

交叉熵

含义： 交叉熵用于度量同一个随机变量X的预测分布Q(X_{i})与真实概率分布P(X_{i})之间的差距。

定义：

离散形式：
$$\begin{gathered} H(P,Q)=-\sum _{i=1}^{n}p(x_i)log(q(x_i)) \\ =\sum _{i=1}^{n}p(x_i)log(\frac{1}{q(x_i)}) \end{gathered}$$
连续形式：
$$\begin{gathered} H(P,Q)=-{\int }_{X}p(x_i)log(q(x_i))dr(x) \\ ={\int }_{X}p(x_i)log(\frac{1}{q(x_i)})dr(x) \end{gathered}$$
结论： 预测越准确，交叉熵越小，其大小只跟真是标签的预测概率值相关。

举个例子：

在深度学习中，假设P表示样本的真实分布（满足(0,1)分布，即真实标签），Q表示神经网络的预测分布（每个类别各自预测的概率）。

那么简单来讲，交叉熵就是计算的真实标签与预测标签之间的差距，交叉熵越小，差距越小。

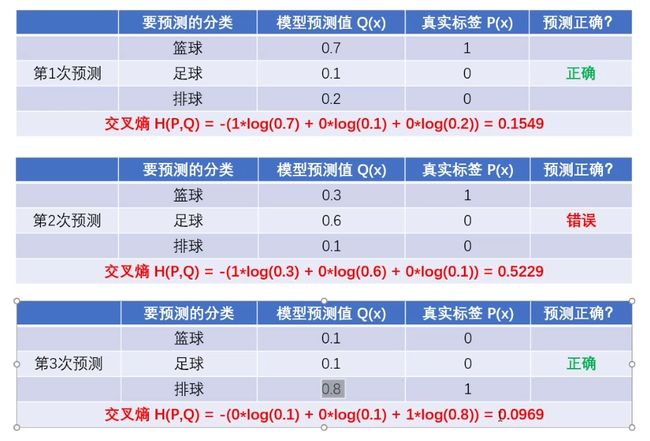
如图所示，真实标签为0的样本，交叉熵计算当中$$0\ast log(q(x_i))$$，相当于排除掉了真实标签为0的样本的真实值与其预测值之间的距离，所以交叉熵的值仅仅等于标签为1的样本的真实值与其预测值之间的距离，即$$H(P,Q)=-(1\ast log(q(x_i))+0+0)=-(1\ast log(q(x_i))$$，此时的交叉熵值越小，说明标签为1的样本的真实值与其预测值之间的距离越小，模型预测的结果越准确，反之，交叉熵就越大，说明模型预测的结果不准确。

交叉熵与KL散度

交叉熵与KL散度一样，同样可以计算同一个随机变量的两个不同概率分布之间的距离，所以交叉熵算是KL散度的一种。

交叉熵与KL散度是有转换关系的：

结论： KL散度=交叉熵-信息熵，因为真实分布已知，所以用交叉熵代替KL散度（KL散度就等于交叉熵），如果不知道真实分布，那就只能用KL散度。

交叉熵损失函数

损失函数衡量的是每个样本预测值和真实值的差值。

深度学习中做分类问题少不了使用交叉熵损失函数，常见的交叉熵损失类型有以下几种：

• 二分类：Sigmoid + Cross-entropy
• 二分类：SoftMax + Cross-entropy
• 多分类：SoftMax + Cross-entropy

二分类用Sigmoid还是SoftMax，SoftMax更多一些。

SoftMax + Cross-entropy：
$$loss(x,class)=-log(\frac{exp(x[class])}{{\sum }_{j}exp(x[j])})=-x[class]+log(\sum _{j}exp(x[j]))$$

• 第一步： SoftMax相当于把数值映射到概率空间，即得到预测分布q(x_i)。

• 第二步： 使用交叉熵公式计算交叉熵损失，目的是为了让交叉熵损失更小，因为交叉熵越小，说明样本的真实值与其预测值之间的距离越小，预测正确的概率越大。

举个例子：

程序计算交叉熵：

entropy = nn.CrossEntropyLoss()
input = torch.Tensor([[
	-0.7715, -0.6205, -0.2562
]])
# 设置第0位为1，其余为0
target =  torch.tensor([0])
output = entropy(input, target)
# 打印输出：1.3447

**注意：**torch.Tensor 与 torch.tensor的区别

torch.Tensor是torch.FloatTensor一个别名，分别使用二者时如下：

torch.Tensor([1,2,3]).dtype
---> torch.float32
torch.tensor([1, 2, 3]).dtype
---> torch.int64
torch.Tensor([True, False]).dtype
---> torch.float32
torch.tensor([True, False]).dtype
---> torch.uint8

手动计算交叉熵：

首先先算真实标签对应数值所占的概率:
$$\begin{gathered} Q(X0)=\frac{exp(-0.7715)}{(exp(-0.7715)+exp(-0.6205)+exp(-0.2562))} \\ =\frac{0.462319}{(0.462319+0.537676+0.773987)}=0.26061087429297 \end{gathered}$$

用交叉熵最简化公式计算交叉熵: 【注意这里log是e为底】
$$H(P,Q)=-log(q(i))=-log(0.26061087429297)=1.344726887$$
可以看出来与程序计算的一模一样。

---