计算矩阵的秩、行空间、列空间、零空间、左零空间
计算矩阵的秩、行空间、列空间、零空间、左零空间
笔记来源:Rowspace and left nullspace | Matrix transformations | Linear Algebra | Khan Academy
秩:求方程组的通解个数、判定非齐次方程组有无解、秩和解的个数有关
零空间:线性方程组 A x = 0 A\boldsymbol{x}=\boldsymbol{0} Ax=0 的所有解的集合
A = [ 2 − 1 − 3 − 4 2 6 ] N ( A ) = { x ∈ R 3 ∣ A x = 0 } A=\begin{bmatrix}2 & -1 & -3\\ -4 & 2 & 6\end{bmatrix}\quad N(A)=\{\boldsymbol{x}\in \mathbb{R}^3 |A\boldsymbol{x}=\boldsymbol{0} \} A=[2−4−12−36]N(A)={x∈R3∣Ax=0}
从矩阵 A A A 化简到上三角矩阵 U U U 再化简到最简行阶梯型 R R R
A x = 0 → U x = 0 → R x = 0 A\boldsymbol{x}=\boldsymbol{0}\rightarrow U\boldsymbol{x}=\boldsymbol{0}\rightarrow R\boldsymbol{x}=\boldsymbol{0} Ax=0→Ux=0→Rx=0
A x = [ 2 − 1 − 3 − 4 2 6 ] [ x 1 x 2 x 3 ] = [ 0 0 ] A\boldsymbol{x}=\begin{bmatrix}2 & -1 & -3\\ -4 & 2 & 6\end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\end{bmatrix}=\begin{bmatrix}0\\ 0\end{bmatrix} Ax=[2−4−12−36]⎣⎡x1x2x3⎦⎤=[00]
[ 2 − 1 − 3 − 4 2 6 0 0 ] → [ 1 − 1 2 − 3 2 − 1 1 2 3 2 0 0 ] → [ 1 − 1 2 − 3 2 0 0 0 0 0 ] \left [ \begin{array}{c:c} \begin{matrix} 2 & -1 & -3\\ -4 & 2 & 6 \end{matrix}& \begin{matrix} 0\\ 0 \end{matrix} \end{array} \right ]\rightarrow \left [ \begin{array}{c:c} \begin{matrix} 1 & -\frac{1}{2} & -\frac{3}{2} \\ -1 & \frac{1}{2} & \frac{3}{2} \end{matrix}& \begin{matrix} 0\\ 0 \end{matrix} \end{array} \right ]\rightarrow \left [ \begin{array}{c:c} \begin{matrix} 1 & -\frac{1}{2} & -\frac{3}{2} \\ 0 & 0 & 0 \end{matrix}& \begin{matrix} 0\\ 0 \end{matrix} \end{array} \right ] [2−4−12−3600]→[1−1−2121−232300]→[10−210−23000]
[ 1 − 1 2 − 3 2 0 0 0 ] [ x 1 x 2 x 3 ] = [ 0 0 ] \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{3}{2} \\ 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\end{bmatrix}=\begin{bmatrix}0\\ 0\end{bmatrix} [10−210−230]⎣⎡x1x2x3⎦⎤=[00]

x 1 x_1 x1是主元变量(与主元相关), x 2 、 x 3 x_2、x_3 x2、x3是自由变量(与主元不相关)
x 1 − 1 2 x 2 − 3 2 x 3 = 0 x 1 = 1 2 x 2 + 3 2 x 3 [ x 1 x 2 x 3 ] = x 2 [ 1 2 1 0 ] + x 3 [ 3 2 0 1 ] x_1-\frac{1}{2}x_2-\frac{3}{2}x_3=0\\ ~\\ x_1=\frac{1}{2}x_2+\frac{3}{2}x_3\\ ~\\ \begin{bmatrix} x_1\\ x_2\\ x_3\end{bmatrix}=x_2\begin{bmatrix}\frac{1}{2}\\ 1 \\0 \end{bmatrix}+x_3\begin{bmatrix}\frac{3}{2}\\ 0 \\1 \end{bmatrix} x1−21x2−23x3=0 x1=21x2+23x3 ⎣⎡x1x2x3⎦⎤=x2⎣⎡2110⎦⎤+x3⎣⎡2301⎦⎤
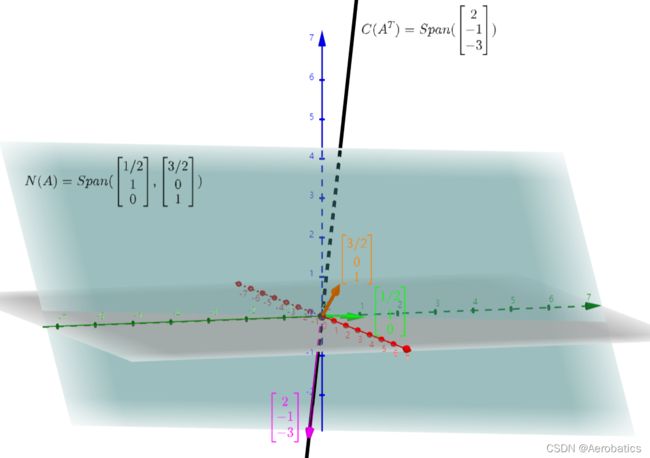
矩阵 A A A 的零空间(要计算矩阵的零空间,需要将矩阵A化为最简行阶梯型矩阵 【reduced row echelon form】,化简后基张成的空间就是矩阵的零空间)
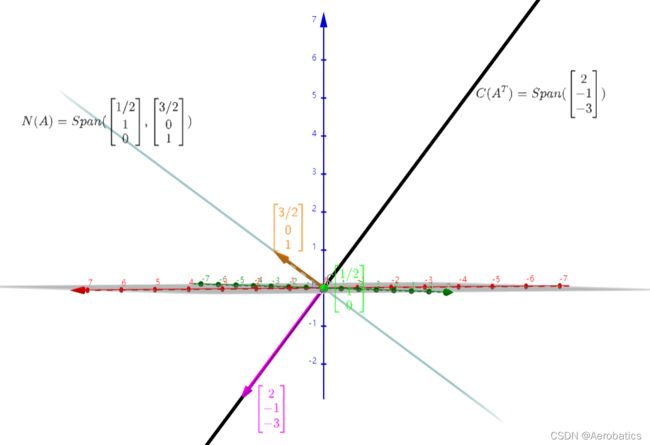
N ( A ) = S p a n ( [ 1 2 1 0 ] , [ 3 2 0 1 ] ) N(A)=Span(\begin{bmatrix}\frac{1}{2}\\ 1 \\0 \end{bmatrix},\begin{bmatrix}\frac{3}{2}\\ 0 \\1 \end{bmatrix}) N(A)=Span(⎣⎡2110⎦⎤,⎣⎡2301⎦⎤)
矩阵 A A A 的列空间(第一个、第二个、第三个向量线性相关,所以只需用一个向量张成的空间即可表达此列空间)
C ( A ) = S p a n ( [ 2 − 4 ] , [ − 1 2 ] , [ − 3 6 ] ) = S p a n ( [ 2 − 4 ] ) C(A)=Span(\begin{bmatrix}2\\ -4\end{bmatrix},\begin{bmatrix}-1\\ 2\end{bmatrix},\begin{bmatrix}-3\\ 6\end{bmatrix})=Span(\begin{bmatrix}2\\ -4\end{bmatrix}) C(A)=Span([2−4],[−12],[−36])=Span([2−4])
矩阵 A A A 的秩(矩阵 A A A化简为最简行阶梯型后非零行的行数或主元个数,几何上表现为经过矩阵A的线性变换后的空间维数)
矩阵 A A A的秩是在回答A中有多少列是线性无关的,矩阵 A T A^T AT是在回答A中有多少行是线性无关的(参考自)
R a n k ( A ) = 1 Rank(A)=1 Rank(A)=1
矩阵 A A A 的转置 A T A^T AT
A T = [ 2 − 4 − 1 2 − 3 6 ] N ( A T ) = { x ∈ R 2 ∣ A T x = 0 } A^T=\begin{bmatrix}2 & -4\\ -1 & 2\\ -3 & 6 \end{bmatrix}\quad N(A^T)=\{\boldsymbol{x}\in \mathbb{R}^2|A^T\boldsymbol{x}=\boldsymbol{0} \} AT=⎣⎡2−1−3−426⎦⎤N(AT)={x∈R2∣ATx=0}
[ 2 − 4 − 1 2 − 3 6 ] → [ 1 − 2 − 1 2 − 1 2 ] → [ 1 − 2 0 0 0 0 ] = r r e f ( A T ) \begin{bmatrix} 2 & -4\\ -1 & 2\\ -3 & 6 \end{bmatrix}\rightarrow \begin{bmatrix} 1 & -2\\ -1 & 2\\ -1 & 2 \end{bmatrix}\rightarrow \begin{bmatrix} 1 & -2\\ 0 & 0\\ 0 & 0 \end{bmatrix}=rref(A^T) ⎣⎡2−1−3−426⎦⎤→⎣⎡1−1−1−222⎦⎤→⎣⎡100−200⎦⎤=rref(AT)
[ 1 − 2 0 0 0 0 ] [ x 1 x 2 ] = [ 0 0 0 ] \begin{bmatrix} 1 & -2\\ 0 & 0\\ 0 & 0 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} ⎣⎡100−200⎦⎤[x1x2]=⎣⎡000⎦⎤
x 1 − 2 x 2 = 0 x 1 = 2 x 2 [ x 1 x 2 ] = x 2 [ 2 1 ] x_1-2x_2=0\\ ~\\ x_1=2x_2\\ ~\\ \begin{bmatrix} x_1\\ x_2 \end{bmatrix}=x_2 \begin{bmatrix} 2\\ 1 \end{bmatrix} x1−2x2=0 x1=2x2 [x1x2]=x2[21]
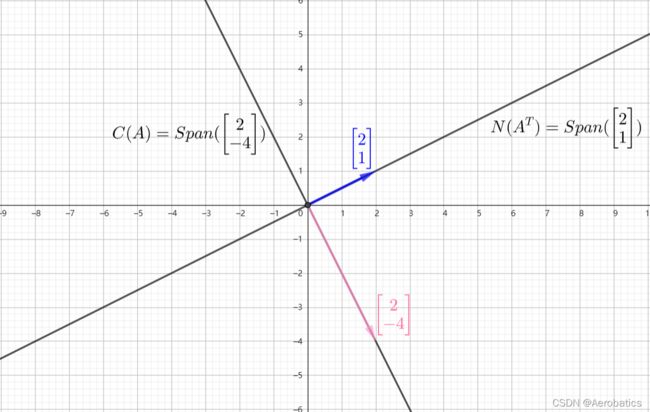
矩阵 A A A 的转置的零空间(即矩阵A的左零空间)(所求的 x \boldsymbol{x} x 在矩阵 A A A 的左侧)
A T x = 0 ( A T x ) T = ( 0 ) T x T ( A T ) T = 0 T x T A = 0 T N ( A T ) = { x ∣ A T x = 0 } = { x ∣ x T A = 0 T } A^T\boldsymbol{x}=\boldsymbol{0}\\ ~\\ (A^T\boldsymbol{x})^T=(\boldsymbol{0})^T\\ ~\\ \boldsymbol{x}^T (A^T)^T=\boldsymbol{0}^T\\ ~\\ \boldsymbol{x}^TA=\boldsymbol{0}^T\\ ~\\ N(A^T)=\{\boldsymbol{x}|A^T\boldsymbol{x}=\boldsymbol{0}\}=\{\boldsymbol{x}|\boldsymbol{x}^TA=\boldsymbol{0}^T\} ATx=0 (ATx)T=(0)T xT(AT)T=0T xTA=0T N(AT)={x∣ATx=0}={x∣xTA=0T}
N ( A T ) = S p a n ( [ 2 1 ] ) N(A^T)=Span(\begin{bmatrix} 2\\ 1 \end{bmatrix}) N(AT)=Span([21])
矩阵A的转置的列空间(即矩阵A的行空间)(第一个向量与第二个向量线性相关,所以只需用一个向量张成的空间即可表达此行空间)
C ( A T ) = S p a n ( [ 2 − 1 − 3 ] , [ − 4 2 6 ] ) = S p a n ( [ 2 − 1 − 3 ] ) C(A^T)=Span(\begin{bmatrix} 2\\ -1\\ -3 \end{bmatrix},\begin{bmatrix} -4\\ 2\\ 6 \end{bmatrix})=Span(\begin{bmatrix} 2\\ -1\\ -3 \end{bmatrix}) C(AT)=Span(⎣⎡2−1−3⎦⎤,⎣⎡−426⎦⎤)=Span(⎣⎡2−1−3⎦⎤)
矩阵 A T A^T AT 的秩(矩阵 A T A^T AT化简为最简行阶梯型后非零行的行数或主元个数,几何上表现为经过矩阵A的线性变换后的空间维数)
矩阵 A A A的秩是在回答A中有多少列是线性无关的,矩阵 A T A^T AT是在回答A中有多少行是线性无关的(参考自)
R a n k ( A T ) = 1 Rank(A^T)=1 Rank(AT)=1
A = [ 2 − 1 − 3 − 4 2 6 ] A T = [ 2 − 4 − 1 2 − 3 6 ] A=\begin{bmatrix}2 & -1 & -3\\ -4 & 2 & 6\end{bmatrix}\quad A^T=\begin{bmatrix}2 & -4\\ -1 & 2\\ -3 & 6 \end{bmatrix} A=[2−4−12−36]AT=⎣⎡2−1−3−426⎦⎤
矩阵 A A A 的零空间 N ( A ) N(A) N(A)、矩阵 A A A 的列空间 C ( A ) C(A) C(A)
N ( A ) = S p a n ( [ 1 2 1 0 ] , [ 3 2 0 1 ] ) C ( A ) = S p a n ( [ 2 − 4 ] ) N(A)=Span(\begin{bmatrix}\frac{1}{2}\\ 1 \\0 \end{bmatrix},\begin{bmatrix}\frac{3}{2}\\ 0 \\1 \end{bmatrix})\quad C(A)=Span(\begin{bmatrix}2\\ -4\end{bmatrix}) N(A)=Span(⎣⎡2110⎦⎤,⎣⎡2301⎦⎤)C(A)=Span([2−4])
矩阵 A A A 的左零空间 N ( A T ) N(A^T) N(AT)、矩阵 A A A 的行空间 C ( A T ) C(A^T) C(AT)
N ( A T ) = S p a n ( [ 2 1 ] ) C ( A T ) = S p a n ( [ 2 − 1 − 3 ] ) N(A^T)=Span(\begin{bmatrix} 2\\ 1 \end{bmatrix}) \quad C(A^T)=Span(\begin{bmatrix} 2\\ -1\\ -3 \end{bmatrix}) N(AT)=Span([21])C(AT)=Span(⎣⎡2−1−3⎦⎤)
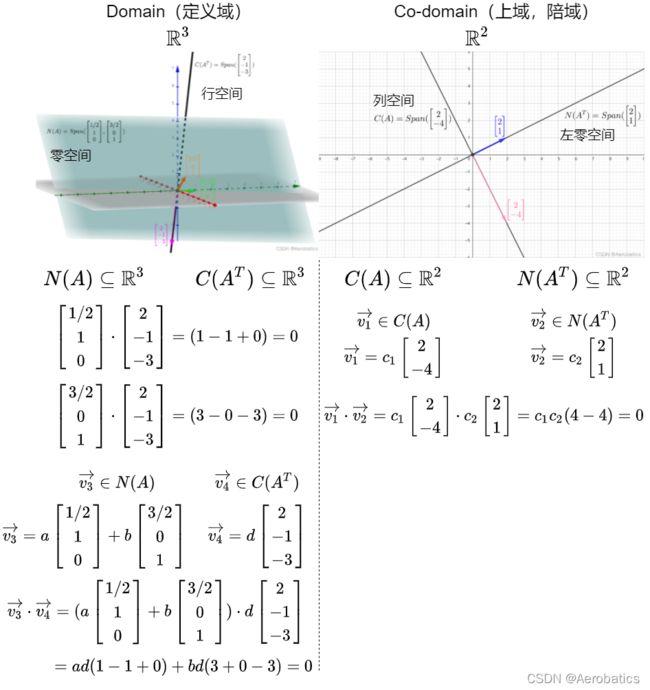
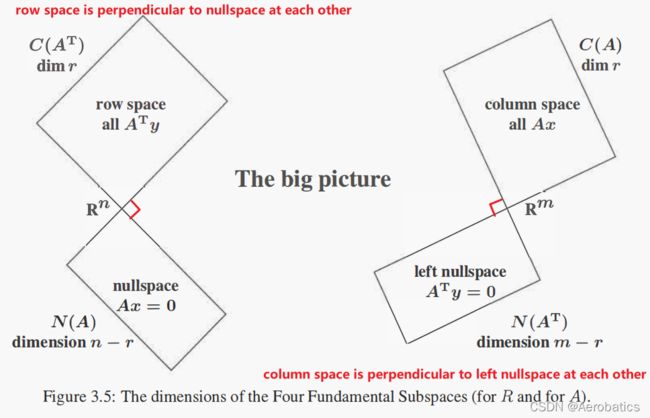
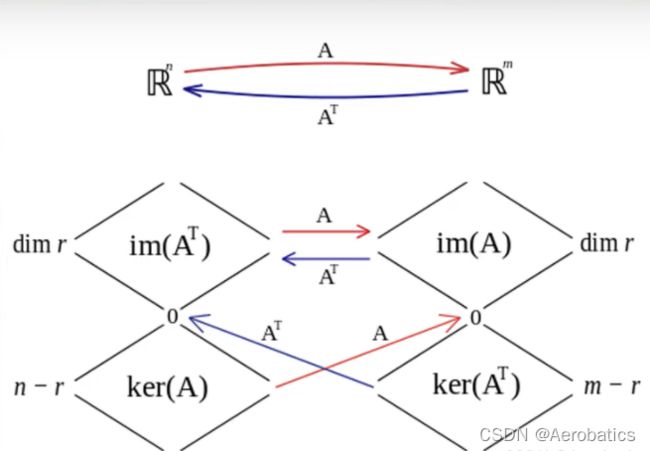
梳理一下各个子空间之间的关系:
矩阵 A A A 的零空间 N ( A ) N(A) N(A) 和 矩阵 A A A 的行空间 C ( A T ) C(A^T) C(AT) 互相垂直
矩阵 A A A 的列空间 C ( A ) C(A) C(A) 和 矩阵 A A A 的左零空间 N ( A T ) N(A^T) N(AT) 互相垂直
矩阵 A A A 的秩为: r = R a n k ( A ) = 1 r=Rank(A)=1 r=Rank(A)=1
矩阵 A A A 的大小:行×列= m × n = 2 × 3 m×n=2×3 m×n=2×3,即 m = 2 m=2 m=2、 n = 3 n=3 n=3

矩阵 A A A 的行空间的维度: r = 1 r=1 r=1 【 C ( A T ) ⊆ R 1 C(A^T)\subseteq \mathbb{R}^1 C(AT)⊆R1】
矩阵 A A A 的零空间的维度: n − r = 3 − 1 = 2 n-r=3-1=2 n−r=3−1=2【 N ( A ) ⊆ R 2 N(A)\subseteq \mathbb{R}^2 N(A)⊆R2】
矩阵 A A A 的列空间的维度: r = 1 r=1 r=1 【 C ( A ) ⊆ R 1 C(A)\subseteq \mathbb{R}^1 C(A)⊆R1】
矩阵 A A A 的左零空间的维度: m − r = 2 − 1 = 1 m-r=2-1=1 m−r=2−1=1【 N ( A T ) ⊆ R 1 N(A^T)\subseteq \mathbb{R}^1 N(AT)⊆R1】