线特征SLAM

线特征

线特征： 优点在于具有天然的光照及视角不变性，同时更高级的特征也使追踪的鲁棒性和准确性有所提高。特别是在特定的人造场景（室内，走廊）等场景，能够克服无纹理或者不可靠纹理带来的干扰。

而其缺点也很明显,在于线段的检测及匹配耗时相对特征点更大。同时在后端也没有一个标准且通用的SLAM优化及回环模块。线特征匹配也是较为困难的，如线段易断裂，不具备强有力的几何约束（如极线几何约束），在纹理缺失处不具有较强的辨识度等。

线特征的典型代表是PL-SLAM，这边文章的链接如下：
PL-SLAM: Real-Time Monocular Visual SLAM with Points and Lines
作者有一个是来自莫斯科三星AI实验室现在去了英国一家slam公司的大神： Alexander Vakhitov
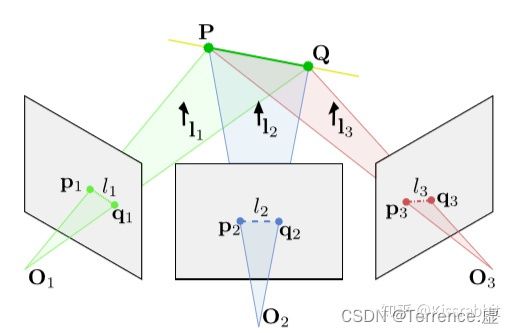
该框架是在ORB-SLAM的框架基础之上，添加了一些与线特征有关的模块，从而构建了一套单目SLAM系统。整个系统的框架如下图所示：

**

摘要

**——众所周知，低纹理场景是依赖点对应的几何计算机视觉算法的主要致命弱点之一，尤其是对于视觉 SLAM。 然而，在许多环境中，尽管纹理较低，但仍然可以可靠地估计基于线的几何基元，例如在城市和室内场景中，或者在结构化边缘占主导地位的所谓“曼哈顿世界”中。 在本文中，我们提出了一种解决方案来处理这些情况。 具体来说，我们建立在 ORB-SLAM 的基础上，大概是当前最先进的解决方案，无论是在准确性还是效率方面，并扩展其公式以同时处理点和线对应。
我们提出了一种解决方案，即使大多数点从输入图像中消失，它也可以工作，而且有趣的是，它可以仅通过检测三个连续帧中的线对应关系来初始化。 我们在 TUM RGB-D 基准测试中彻底评估了我们的方法和新的初始化策略，并证明了线的使用不仅提高了原始 ORB-SLAM 解决方案在纹理不良帧中的性能，而且在序列帧中系统地改进了它 结合点和线，不影响效率。

**

内容

**

一、基于线的SLAM

对于线的描述，采用了 端点(endpoints) 的方法，毕竟现实中，几乎不不可能碰到无限延伸的直线，几乎都是线段，所以，用端点的方法来描述直线是比较合理的。我们假设$P,Q\in R^3$ 是空间直线的两个端点，$p_d,q_d\in R^2$ 是其在图像中的投影坐标，另外，记 $p_d^h,q_d^h\in R^3$ 是对应的齐次坐标。于是，我们可以得到直线的参数：
$I=\frac{p_d^h\times q_d^h}{|p_d^h\times q_d^h|}$ 。

说明：（对于向量(x,y,1)，可以在几何意义上理解为是在【第三维为常数的】平面上的一个二维向量。这种用【三】维向量表示【二】维向量，或者一般而言，用一个n+1维的向量表示一个n维向量的方法称为齐次坐标表示法。】）。

这样我们就可以得到线特征所需要的参数。然后是定义线的重投影误差（line reprojection error） ——投影线段的端点与在图像中检测到的直线之间的点到直线距离 之和：
$E_{\text{line }}(P,Q,I,\theta ,k)=E_{pl}^2(P,I,\theta ,k)+E_{pl}^2(Q,I,\theta ,k)。$ 而 $E_{pl}=I^T\pi (P,\theta ,K)$。
而$E_{pl}=I^T\pi (P,\theta ,K)$ 。

其中，$I$ 为上面提到的直线参数，$\pi (P,\theta ,K)$ 为空间点 投影到图像平面的坐标，而其中的 分别为相机的外参 和内参。理想情况下，空间点 的投影点是在直线上的，所以点到直线距离 $E_{pl}=0$，或者说，点在直线上。

通过这样的计算就可以获取到两条线之间的重投影误差了。

但是，在实际情况中，总会存在线之间有遮挡、误检测等状况，所以，我们在图像中检测到的端点 $p_d,q_d$ 可能与空间直线端点 $P,Q$ 在图像中的投影点不匹配，所以，这里还要定义一个“检测到的线的重投影误差”（detected line reprojection error）：

$E_{\text{line },d}\left(p_d,q_d,I\right)=E_{pl,d}^2\left(p_d,I\right)+E_{pl,d}^2\left(q_d,I\right)$
而 $E_{pl,d}=I^T{p}_d$

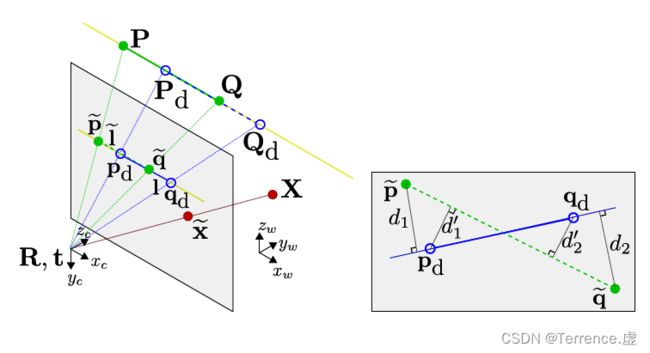
左图： $\mathbf{P},\mathbf{Q}\in {\mathbb{R}}^3$ 表示3D线特征上的两个3D点，$\mathbf{p},\mathbf{q}\in {\mathbb{R}}^2$ 是他们在image 图像平面上的投影点，$\tilde{l}$ 是投影的线的系数。

${\mathbf{p}}_{\mathrm{d}},{\mathbf{q}}_{\mathrm{d}}\in {\mathbb{R}}^2$ 是提取出的线特征（线段）的两个端点，也就是我们所说的measurements 测量值， ${\mathbf{P}}_{\mathrm{d}},{\mathbf{Q}}_{\mathrm{d}}\in {\mathbb{R}}^3$就是这两个端点反投影回到3D空间中对应的3D点， I 是检测到的线的系数。
红色那条线是一个点特征的投影模型， $\mathbf{X}\in {\mathbb{R}}^3$ 是一个3D点， 对应的$\mathbf{x}\in {\mathbb{R}}^2$

二、基于线和点的BA

我们定义 $X_j\in R^3$ 为地图上的第$j$个点。对于第$i$个关键帧，$X_j$ 在该图像平面中的投影点为：
${\tilde{x}}_{i,j}=\pi \left(X_j,{\theta }_i,K\right)$

其中，${\theta }_i$ 为第$i$个关键帧的外参。对于给定的观测点 $x_{i,j}$ ，我们可以定义如下的3D误差：$e_{i,j}=x_{i,j}-{\tilde{x}}_{i,j}$
类似的，我们可以定义第j个地图中的线段的端点 $P_j,Q_j$ 。其在第i个关键帧中的投影坐标（采用齐次坐标形式）记为：
${\tilde{p}}_{i,j}^h=\pi \left(P_j,{\theta }_i,K\right)$
${\tilde{q}}_{i,j}^h=\pi \left(Q_j,{\theta }_i,K\right)$

然后，对于给定的所观测到的第$j$个直线端点 $p_{i,j},q_{i,j}$ ，然后计算出观测到直线的参数 ${\tilde{I}}_{i,j}$ ，则误差向量可以定义为：
$e_{i,j}^{\prime }={\left({\tilde{I}}_{i,j}\right)}^T\left(K^{-1}{p}_{i,j}^h\right)$
$e_{i,j}^{\prime \prime }={\left({\tilde{I}}_{i,j}\right)}^T\left(K^{-1}{q}_{i,j}^h\right)$

(PS：这个$e_{i,j}^{\prime },e_{i,j}^{\prime \prime }$ 的定义我个人认为是不对的，因为$p_{i,j}^h$ 既然是图像坐标，那么乘以 $K^{-1}$ 的结果就是相机坐标系归一化平面中的坐标，而不再是图像平面中的了，所以，这就和在图像平面中的直线参数 ${\tilde{I}}_{i,j}$ 的乘积的物理意义就不对了，所以，个人认为，不应该有这个$K^{-1}$)

关于这一点，在后面的雅克比求解过程中也会体现出来。

于是，我们最终的误差目标函数就可以写成：
$C={\sum }_{i,j}\rho \left({\mathbf{e}}_{i,j}^{\top }{\Omega }_{i,j}^{-1}{\mathbf{e}}_{i,j}+{\mathbf{e}}_{i,j}^{\prime }{}^{\top }{\Omega }_{i,j}^{\prime }{}^{-1}{\mathbf{e}}_{i,j}^{\prime }+{\mathbf{e}}_{i,j}^{\prime \prime }{\Omega }_{i,j}^{\prime \prime }{}^{-1}{\mathbf{e}}_{i,j}^{\prime \prime }\right)$

其中，$\rho (\cdot )$ 为鲁棒代价函数，文中使用的是Huber。${\Omega }_{i,j},{\Omega }_{i,j}^{\prime },{\Omega }_{i,j}^{\prime \prime }$ 为关键点和线段端点在不同尺度下的协方差矩阵。