Parl 强化学习7日打卡营学习后记

前言

百度AIStudio平台上发布了NeurlPS团队7日全直播教学，含5次实战打卡，带你从零实践强化学习。学习内容包含了强化学习的基本原理，几种常见的强化学习方法的介绍，主要采用Parl的框架进行RL的程序搭建。
学习平台：百度AIStudio
Python: paddle、parl、gym、atari-py、rlschool、numpy

概述

只需要有概率论知识基本能够很轻松地理解RL学习的原理，本次课程上涉及的数学公式不多，即使有不懂的在课程的直播中老师也有给予足够的解释说明。
即使对数学原理细节不太清晰，对于实际应用Parl不造成太大的影响。
本次课程包含了：Sarsa、QLearning、DQN、PG、DDPG五种学习策略。其中Sarsa和Qlearning是用于初步进入强化学习的领域，不需要用到神经网络就能直接实践操作。
因为RL学习基于的就是人类的经验学习，在整个课程当中，不管哪种策略原理都是非常直观。所以在原理方面我在此就不做过多的陈述。
这里的记录主要是在个人学习过程中觉得需要理解清楚的问题和我对此问题的理解或者解决思路。

记录

Table Q

前面基于Q表格方式的学习策略都比较轻松就能理解并且根据原理重新复写代码。

Sarsa、QLearning

Gamma公式展示 $\Gamma (n)=(n-1)!\forall n\in \mathbb{N}$ 是通过欧拉积分
Sarsa、QLearning：主要区别在于“学习资料”的不同
Sarsa：使用了下一状态的Q动作进行训练（on-policy）
$$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha [R_{t+1}+\gamma Q\left(S_{t+1},A_{t+1}\right)-Q\left(S_t,A_t\right)]$$
QLearning：使用了下一状态实际动作进行训练（off-policy）
$$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha [R_{t+1}+\gamma \underset{a}{\max }Q\left(S_{t+1},a\right)-Q\left(S_t,A_t\right)]$$
（有“实际动作”之称是因为用了Epsilon-Greedy方式进行动作探索：如果没有贪心算法进行随机探索，AI是不会往外试错的。）

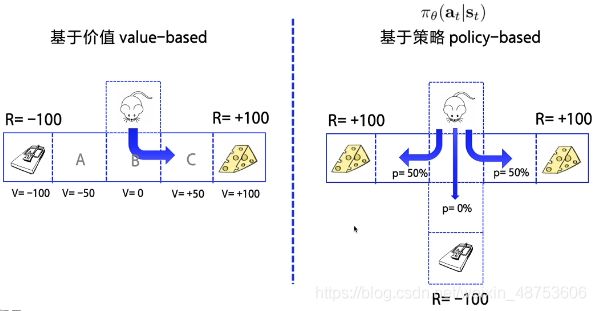
避免造成误会，注释一下：off-policy是指学习中不采用探索策略，选择目前Table Q里面的最好选择。实际上这里两个方式都是Value_Based。

DQN

DQN就是为解决传统Table Q会随着动作自由度和状态多样性的增加而成倍增长问题，采用神经网络的方式将环境和动作都处理成实数域。近似的环境、动作在数值上也是近似的。
引入了固定Q表格和经验回放的方法。

这里提到了Q-Target,字面意义上是目标Q，它是滞后于实际学习更新的Table Q，代码中的作用是用于Off-Policy时取出一个确切的动作，然后将此环境的各动作Q值跟Table-Q的One-Hot化动作求这一动作的Q值，后再与Q-Target进行MSE运算，作为Loss。Q-Target在此DQN里面是才去硬更新的方式，RL过程中的学习不更新Q-Target。

PARL强化学习公开课Lesson3_DQN课程 部分代码（Car-Pole）

def learn(self, obs, action, reward, next_obs, terminal):
        """ 使用DQN算法更新self.model的value网络
        """
        # 从target_model中获取 max Q' 的值，用于计算target_Q
        next_pred_value = self.target_model.value(next_obs)
        best_v = layers.reduce_max(next_pred_value, dim=1)
        best_v.stop_gradient = True  # 阻止梯度传递
        terminal = layers.cast(terminal, dtype='float32')
        target = reward + (1.0 - terminal) * self.gamma * best_v

        pred_value = self.model.value(obs)  # 获取Q预测值
        # 将action转onehot向量，比如：3 => [0,0,0,1,0]
        action_onehot = layers.one_hot(action, self.act_dim)
        action_onehot = layers.cast(action_onehot, dtype='float32')
        # 下面一行是逐元素相乘，拿到action对应的 Q(s,a)
        # 比如：pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
        #  ==> pred_action_value = [[3.9]]
        pred_action_value = layers.reduce_sum(
            layers.elementwise_mul(action_onehot, pred_value), dim=1)

        # 计算 Q(s,a) 与 target_Q的均方差，得到loss
        cost = layers.square_error_cost(pred_action_value, target)
        cost = layers.reduce_mean(cost)
        optimizer = fluid.optimizer.Adam(learning_rate=self.lr)  # 使用Adam优化器
        optimizer.minimize(cost)
        return cost

个人理解：这里的Q-Target算出来的target和Table-Q算出来的实际动作pred_action_value进行MSE是保证Table-Q的学习总是往Q-Learning的公式更新$Q(S_t,A_t)$进发
固化Q作为标的的目的是减轻学习更新产生的抖动对学习的总体稳定产生的影响。

Policy-Gradient

前面课程提到的Q-Table方式都是针对离散动作的强化学习。
这里开始就是Policy-Based策略。主要要理解的是MDP，这里提供一个比较清晰的MDP马尔科夫决策过程说明。
值得注意的是这里面只是开始讲述Policy-Based方式，里面说解决连续控制版本的CartPole问题实际上课程代码上还是给出离散动作环境的CartPole，并非连续动作。这一点和直播提到的RL环境不一样。
课程作业中主要遇到的问题是在Atari的Pong环境下，不清楚在哪里做错了修改，导致算法收敛效果不好，经过回复初始版本再回填Model、Algorithm、Agent也会时不时出现练习上千个Round都学习不到胜利的策略。
感觉只能通过多次的训练，寄希望于出现偶尔探索出会胜利的模型，然后再在此模型基础上进行下一步调参深化学习。
目前通过调高Model网络层元素，从60到128后可以稳定训练出可用再练模型。
这个Pong的环境个人经验需要大学习率跳过“洼地”，之后再调低学习率进行下一步学习会明显加快学习速度。
在paddle.fluid.layer里面有专门的Learning-Rate Decay工具exponential_decay、inverse_time_decay、natural_exp_decay可以调入。
个人理解：如果能够直接每一场比赛里面的每次进球进行学习应该会更加高效，因为reward是以进球来给的，如此一来可以具体地让每一球的每一个动作都进行对该场次的特定学习。因为每一球进入获得+1的时刻，该动作其实和进球没有任何关系。（球早就被撞出去了。）而只有-1时刻的动作和输球有直接关系。这里的课程用calc_reward_to_go的方式，把Reward衰减来近似分隔每一球。根据不同的环境应该进行相应的reward微调，从而增加学习的效率，或者实现更少step获取胜利。事实上的训练中由于把21球当作一个Round每次训练的时间会先提高后降低，容易进入僵直状态导致学习进行缓慢。
另外一提，这里的Lost采用Entropy_Cross_Cost是用于让动作向稳定的动作发展。因为Policy_Based给出的是动作概率，并非确定动作，概率越接近One_Hot，动作越稳定。

Deep Deterministic Policy Gradient

课程代码展示的是gym的Cartpole连续控制版。
这个算法比较容易理解，利用到Actor-Critic结构。
主要就是进行分工，Actor负责动作的确定，Critic负责环境的确定。
Critic将所有因素归结起来打分输出为自己的Reward。
Actor则将Critic的Reward进行解读决策向量动作。
这里也利用到了DQN的固定Q和经验回放。
基本没什么问题，需要注意的是作业代码中关于用于经验学习所记录的动作应该是action_mapping之前的action。因为Actor的Out是选择了tanh为激活函数。
如果没有修改这一层，怎么练都练不出来。原代码的方式稳定学习了就能够获得8k左右的Test Reward。
另外，得到了已经相对稳定的Model参数之后再训练的过程中除了学习率要修改，也一定要把白噪声降低进行Train，因为模型基本能够稳定好自己，只需要小范围的探索就能进行更进一步的稳定。
如果用到另一个同学所说的将Action提升至5个参数，1个负责基础电压，另外四个分别负责Offset，能够稳定上升到9K的Reward。
值得注意的是：Parl的DDPG算法里面不能使用学习率衰减，在DDPG的__init__里面将传入的lr都进行了assert isinstance(lr，float)。按理来说修改DDPG过后是可以使用的，至于专门进行限制，我不清楚是出于什么原因。