特征筛选方法--卡方检验

1. 信息包含量指标

首先，最为通用、且往往用于特征筛选的第一步的特征有效性评估指标，就是特征的信息包含量指标。很明显，且不论所包含信息是否有效，如果特征本身包含信息有限甚至是根本就不包含任何有效信息，则需要在特征筛选的第一个环节就被快速的剔除，以提升后续进行特征有效性识别与筛选的效率。

而对于特征所包含信息量的识别也并不复杂，我们可以通过两个指标的计算来进行判断，其一是特征的缺失值所占比例，其二是单变量的方差。对于某个特征来说，如果缺失值占比过大（如超过90%），除非从业务角度判断可以通过标记法进行填补，否则可以视作特征信息大范围缺失，是没有进一步分析必要的，可以直接剔除；其次，对于不包含缺失值的字段，我们也可以通过方差对其包含信息量进行识别，一般来说方差越小、特征包含的信息量就越少，极端情况下，方差取值为0时，该特征所有取值都一样，也就相当于不包含任何有效信息，是需要被快速识别和剔除的。

1.1 缺失值比例计算与特征筛选

def MissingValueThreshold(X_train_temp, X_test_temp, threshold = 0.9, fn = 0):
    """
    根据比例删除缺失值比例较高的特征
    同时将其他缺失值统一填补为fn的值
    
    :param X_train_temp: 训练集特征
    :param X_test_temp: 测试集特征
    :param threshold: 缺失值比例阈值
    :param fn: 其他缺失值填补数值
    
    :return：剔除指定特征后的X_train_temp和X_test_temp
    """
    for col in X_train_temp:
        if X_train_temp[col].isnull().sum() / X_train_temp.shape[0] >= threshold:
            del X_train_temp[col]
            del X_test_temp[col]
        else:
            X_train_temp[col] = X_train_temp[col].fillna(fn)
            X_test_temp[col] = X_test_temp[col].fillna(fn)
    return X_train_temp, X_test_temp

1.2 单变量方差与特征筛选

我们进一步考虑单变量方差的计算过程与特征筛选过程，该过程要求先单独对数据集的每一列进行方差计算，然后根据给出的阈值剔除那些方差没达到阈值的列。该过程可以借助sklearn中的VarianceThreshold评估器快速实现。

from sklearn.feature_selection import VarianceThreshold
"""
VarianceThreshold评估器有且只有一个参数，即方差阈值，
需要注意的是，只有某列的方差大于该阈值，才能被保留，
而小于或等于该阈值的方差对应的列都会被剔除：
"""
# 实例化评估器
sel = VarianceThreshold(threshold=0) #剔除哪些方差为0的连续、离散特征
# 训练评估器，对数据集进行修改
sel.fit_transform(df_temp)
df_temp.columns[sel.variances_ != 0]
df_temp[df_temp.columns[sel.variances_ != 0]]
"""
此外需要注意的是，由于我们往往希望保留剔出特征后的列名称，
而上述评估器最终输出结果是一个array，
我们需要借助VarianceThreshold评估器的variances_属性，
来查看每一列的方差计算结果，并据此推算剔除和保留的列，并最终给保留列赋予列名称：


需要注意的是，特征的方差会显著的受到特征取值大小的影响，
即某特征本身取值较大，方差计算结果也越大，
例如某列取值放大10倍，则方差会放大100倍：
因此，很多时候对于连续变量来说，除非我们很明确各连续特征的量纲一致，
否则设置阈值筛选特征的意义不大，
更多的时候我们是使用VarianceThreshold默认参数剔除哪些方差为0的连续特征。

既然取值大小会影响方差计算结果，那能不能通过标准化消除这种影响呢？
答案是肯定不行。如果是Z-Score标准化，
则会将特征转化为均值为0、标准差为1的特征，
此时除了原本方差为0的特征，其他所有特征的方差都会转化为1：
"""

2. 特征和标签关联度指标

• 判断特征包含信息“是否有用”

第一部分的信息包含量指标重点衡量的是特征包含的信息量大小，而本部分开始介绍的指标，则是用于衡量特征所包含的这些信息是否有用。

2.1 借助sklearn进行特征评估及筛选

• r_regression评分函数

"""
我们也可以借助sklearn中相关功能实现，首先sklearn中的相关系数计算函数为r_regression：
"""
from sklearn.feature_selection import r_regression
from sklearn.feature_selection import SelectKBest
r_regression(X_train, y_train )
"""
array([-0.01860513,  0.14016383, -0.15957745, -0.15254382, -0.00250081,
        0.0315595 , -0.05444391, -0.30748405, -0.19723667, -0.19116379,
       -0.2888665 , -0.03987906, -0.05014176, -0.39446444,  0.18666114,
        0.11637491, -0.35726337,  0.18182966, -0.21023844])
"""
KB = SelectKBest(r_regression, k=10)
X_new = KB.fit_transform(X_train, y_train)  #得到一个只有10个（经过排序最大）特征的新数据
"""
有两点需要注意，首先，SelectKBest只会根据输入函数的评分按照由高到低进行筛选，
因此此处输出的特征只是相关系数最大的10个特征，
并不是相关系数绝对值最大的10个特征；
其次，返回结果的特征排序其实是原始特征在剔除了那些评分未进前10的特征之后的特征，
并不是按照评分由高到低排名的前10个特征。
"""
#将筛选后列名称的提取过程封装为一个函数：
def SelectName(KB):
    """
    根据特征筛选评估器进行列名称输出函数
    
    :param KB: 训练后的BestK特征筛选评估器
    
    :return：保留特征的列名称
    """
    threshold = sorted(KB.scores_, reverse=True)[KB.k - 1]
    
    col_names = []

    for score, col in zip(KB.scores_, KB.feature_names_in_):
        if score >= threshold:
            col_names.append(col)
            
    return col_names
col_names = SelectName(KB)
X_train_new = pd.DataFrame(X_new, columns=col_names)
#这就得到一个dataframe

• f_regression评分函数

如果是计算相关系数，其实正负相关性都是可以使用的，也就是说我们更希望这个过程是一个先计算绝对值、再进行特征筛选的过程。此时如果要实现该功能，则需要借助sklearn中的另一个评分函数：f_regression

from sklearn.feature_selection import f_regression

"""
从使用角度来说，f_regression的本质就是评估两列的相关性，
如果考虑到评分的数值结果，则从数值大小顺序上来说，
就相当于相关系数取绝对值后排序结果
"""
f_regression(X_train, y_train)
KB = SelectKBest(f_regression, k=10)
X_new = KB.fit_transform(X_train, y_train)
col_names = SelectName(KB)
X_train_new = pd.DataFrame(X_new, columns=col_names)

• SelectPercentile按比例筛选特征

除了可以筛选评分最高的k个特征，还可以按照比例进行筛选。此时就需要用到SelectPercentile评估器了

from sklearn.feature_selection import SelectPercentile

SP = SelectPercentile(f_regression, percentile=30) #考虑筛选评分前30%的特征
SP.fit(X_train, y_train)
SP.transform(X_train)

# 修改SelectName函数，使其能够基于SelectPercentile的筛选结果输出列名称
def SelectName(Select, KBest=True):
    """
    根据特征筛选评估器进行列名称输出函数
    
    :param Select: 训练后的特征筛选评估器
    :param KBest: 是否是挑选评分最高的若干个特征
    
    :return：保留特征的列名称
    """
    if KBest == True:
        K = Select.k
    else:
        l = np.array(range(Select.n_features_in_))
        K = (l > np.percentile(l, 100 - Select.percentile)).sum()
    
    threshold = sorted(Select.scores_, reverse=True)[K-1]
    
    col_names = []

    for score, col in zip(Select.scores_, Select.feature_names_in_):
        if score >= threshold:
            col_names.append(col)
            
    return col_names

SP = SelectPercentile(f_regression, percentile=35).fit(X_train, y_train)
X_new = SP.transform(X_train)
X_train_OE[SelectName(SP, KBest=False)].head()

在实际进行筛选时，最重要的一点就是关于评分函数的选择。通过查看sklearn的说明文档，sklearn中至少提供了五种常用的特征评分函数，并且围绕不同问题（分类还是回归），建议选择不同的评分函数：

从严格意义上来说，相关系数只能衡量连续变量的同步变化趋势，很多分类问题采用相关系数进行衡量并不能得到一个很好的结果。更进一步说，在大多数情况下，根据指标进行特征筛选的结果好坏的根本往往就在于评分函数的选取，因此接下来，我们重点介绍不同评分函数的计算流程和使用场景，这里需要注意的是，由于根据评分进行特征筛选本质上是一个“先验”的过程，很多评分指标背后都有非常强的统计学背景，此处仅从机器学习算法的使用角度切入进行介绍，并补充必要的统计学知识。

• 卡方检验

在一般情况下，卡方检验是针对于离散变量的独立性检验，卡方检验的零假设为两个离散变量相互独立。很明显，如果我们将其用于标签和特征的判别，就能借此判断某特征和标签是不是独立的，如果是，则说明特征对标签的预测毫无帮助。因此在很多时候，卡方检验都是非常重要的剔除无关特征的方法.

1. Step 1.提出假设
   $$H_0:Contract字段和标签相互独立$$
   $$H_1:Contract字段和标签不相互独立$$

2. Step 2.采集数据

对于Contract字段来说，按月付费用户为0、年度付费用户标记为1、两年一次付费用户标记为2。标签是Churn代表是否流失，0表示未流失、1表示流失：

df_count = pd.crosstab(y_train, X_train_OE['Contract'])

3. Step 3.设计统计量

df_count_all = df_count.copy()

df_count_all.loc['Contract-all'] = df_count.sum(0)
df_count_all['Churn-all'] = df_count_all.sum(1)
df_count_all

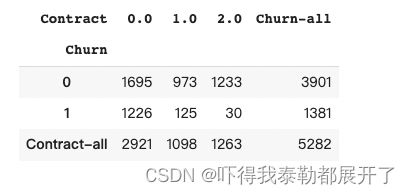
现在，我们假各变量总体数据分布不变，即Contract总共是有三个不同取值，Contract=0有2921位用户、Contract=1有1098名用户、Contract=2有1263名用户，而Churn有两个不同取值，Churn=0有3901名用户、Churn=1有1381名用户。在此统计结果基础上。

取值分布如下：
$$P(Contract=0)=\frac{2921}{5282}\approx 0.553$$
$$P(Contract=1)=\frac{1098}{5282}\approx 0.2078$$
$$P(Contract=2)=\frac{1263}{5282}\approx 0.2391$$
同时，ℎ的取值分布如下：
$$P(Churn=0)=\frac{3901}{5282}\approx 0.7385$$
$$P(Churn=1)=\frac{1381}{5282}\approx 0.2614$$
现依据零假设，和ℎ相互独立，因此对于任意一名用户，同时=0且ℎ=0的概率为：
$$P(Contract=0,Churn=0)=P(Contract=0)\ast P(Churn=0)=0.533\ast 0.7385=0.39$$

根据联合概率计算公式，当A、B两个随机变量相互独立时，$P(A,B)=P(A)\ast P(B)$

而目前，总共有5282名用户，因此在零假设的情况下，=0且ℎ=0的用户总数期望为：

$$E_{0,0}=P(Contract=0,Churn=0)\ast 5282=0.39\ast 5282=2060$$

而真实的统计结果是=0且ℎ=0总用户有1695，和期望人数有些差异，很明显，当实际人数和期望人数的差异越大，我们就越有理由怀疑零假设。但这种差异是不能通过和ℎ的一组取值结果来判定，我们还需要进一步查看列联表中其他位置的期望频数。

Contract_all = df_count_all.loc['Contract-all', :].copy()
Contract_all
"""
Contract
0.0          2921
1.0          1098
2.0          1263
Churn-all    5282
"""
Churn_all = df_count_all.loc[:, 'Churn-all'].copy()
Churn_all
"""
Churn
0               3901
1               1381
Contract-all    5282
"""
tol = 5282

对于每个单元格，期望频数的计算应该是$(\frac{Churn\_all[i]}{tol})\ast (\frac{Contract\_all[j]}{tol})\ast tol$，等于$\frac{Churn\_all[i]\ast Contract\_all[j]}{tol}$

for i, j in product(range(2), range(3)):
    Eij = Churn_all[i] * Contract_all[j] / tol
    df_count_temp.iloc[i, j] = Eij
df_count_temp
"""
Contract	0.0	1.0	2.0
Churn			
0	2157.292881	810.923514	932.783605
1	763.707119	287.076486	330.216395
上（期望）
--------------------------------------
这是期望的频数表，要和之前的频数表衡量差异
--------------------------------------
下（真实）
Contract	0.0	1.0	2.0
Churn			
0	1695	973	1233
1	1226	125	30
"""

为了衡量二者的差异，我们可以构造如下统计量
$${\mathcal{X}}^2=\sum _{i=1}^m\sum _{j=1}^n\frac{(O_{i,j}-E_{i,j}{)}^2}{E_{i,j}}$$
其中i、j代表列联表的行和列，$O_{i,j}$表示i行j列的观测值（observe）、$E_{i,j}$表示期望值。而此处的${\mathcal{X}}^2$就是卡方值，也就是卡方检验中的统计量。我们可以通过如下方式进行卡方值的计算：

np.sum(np.power(df_count_temp - df_count, 2) / df_count_temp).sum()
"""
872.369407342287

"""

很明显，${\mathcal{X}}^2$越大，说明实际结果和期望结果差异越大，当然这里也会受到单元格数量的影响，因此我们需要用某种方式表示单元格对其的影响，对于卡方检验来说，就是所谓的自由度（degree of freedom，简称df或者dof），其影响的具体表现稍后再说，这里我们先介绍卡方检验的自由度的计算方式，对于二维列联表来说，自由度就是$(m-1)\ast (n-1)$，行数-1和列数-1的乘积：

(2-1) * (3-1)
"""
2
"""

即完整的卡方统计结果的表示方法如下:
$${\mathcal{X}}^2(2)=872.369407342287$$

对于卡方统计表，首先我们找到自由度为2的一行，然后我们发现${\mathcal{X}}^2(2)=0.01$的概率为0.995，也就是说如果卡方统计结果为0.01，则99.5%的概率带入检验的两列相互独立，而伴随着卡方值越来越大，相互独立的概率也随之减少，例如当卡方值增长到4.6时，只有0.1的概率二者相互独立，而当卡方值取到13.82时，只有0.01的概率二者相互独立。很明显，此时卡方值为872，说明Contract和Churn相互独立的概率不到0.01。据此我们就有充分的理由拒绝零假设，即Contract和Churn并不是相互独立的。而基于该推论，我们也就得出了针对特征筛选环节的最终结论——保留Contract列。

此外，通过观察卡方分布表我们也发现，自由度越大，卡方检验对频数分布的期望与实际层面的差异的容忍度越高。具体原因不必深究，但需要注意的是自由度是会影响随机变量的概率分布的，不仅卡方值是如此，其他很多随机变量也是如此。

• 借助sklearn进行卡方检验特征筛选

from sklearn.feature_selection import chi2

chi2_p = chi2(x_train[discrete_cols], y_train)[1]  #chi2会输出卡方值和p值（就是显著性水平）
chi2_discrete_cols = []

for pValue, colname in zip(chi2_p, discrete_cols):
    if pValue < 0.01:  #把显著性水平小于0.01，即是相互独立的可能性为小于0.01的筛选出来
        chi2_discrete_cols.append(colname)
print(chi2_discrete_cols)