《数据科学R语言实践：面向计算推理与问题求解的案例研究法》一一2.4 探索所有男选手的跑步时间...

本节书摘来自华章计算机《数据科学R语言实践：面向计算推理与问题求解的案例研究法》一书中的第2章，第2.4节,作者：[美]　德博拉·诺兰（Deborah Nolan）　　邓肯·坦普·朗（Duncan Temple Lang）　 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

2.4　探索所有男选手的跑步时间

现在我们已经完成了对公布在Cherry Blossom网站上表格数据的提取，可以开始研究年龄和跑步时间之间的关系了。典型地，我们首先以图形化的方式考查构建在散点图上的数据，其中散点图以跑步时间为y轴，年龄为x轴。下面我们调用plot()函数对男运动员构造这样的一张散点图。

这里我们使用一个轴范围参数ylim，以筛选掉诸如跑步时间为1.5分钟这类的参赛者。
在对plot()的调用中，第一个参量是R公式。R的公式语言非常强大，它可以简洁地表达复杂的关系，各种R函数都可以解释一个公式并相应地对数据进行分析。在本例中，这个公式非常简单，runTime ~ age，它表示我们对runTime如何依赖于age，或者runTime随age如何变化感兴趣。plot()函数根据数据的表示来构建可视化模型。runTime和age都是数值型变量，plot()绘制一个以runTime为y轴，age为x轴的散点图。在本节的稍后部分，我们将会看到其他的包含类别变量等更多变量的公式，也会看到用于如lm()和loess()等其他函数的公式。
绘制结果如图2-6所示。由于大量的数据点相互重叠，导致散点图上的大多数点形成了黑色的一团。分布的形状显得模糊，因为我们看不到在（age，run time）空间的哪些区域的密度更大。注意图中还出现了一些垂直条纹，这些条纹的形成主要是由于参赛选手的年龄一直被记录到了最近一个年份，这样导致了过度的重叠绘制。在下一节，我们将考虑对默认的散点图构建方法进行一些改进以解决重叠绘制的问题。
2.4.1　根据大量观察绘制散点图
我们可以对图2-6中绘制的散点图做一些改变以改善其过度重叠的效果。我们可以减小绘图符号的尺寸，对绘图符号采用透明的颜色，以及对年龄变量添加少许的随机噪声。另外，我们还可以创建一个对每个区域点的密度进行平滑的绘图版本，也可以绘制一系列的箱线图来代替散点图。本节我们将逐一演示以上的绘图方法。
首先，我们修改对plot()的调用，把图中的点标识由圆圈改为圆点，同时缩小圆点的尺寸，并用透明的蓝色作为圆点的颜色。如果我们对绘图符号采用透明颜色，当两个符号点重叠时，它们的颜色就会变深，这样高密度的区域会比低密度的区域颜色更深。

图2-6　男选手的跑步时间对年龄的默认散点图。该图显示70 000名男选手的跑步时间对于年龄的一个简单散点图，图中导致了如此严重的重叠绘制，以致于数据的形状无法辨识
在R语言和其他一些系统中，颜色可以通过多种方式进行指定。RGBA规范提供了用以合成一种颜色的红-蓝-绿组成的三元组，该规范中的第四个成分给出了透明度的数值。可以从RcolorBrewer程序包提供的Cindy Brewer调色板中选取一个颜色[2]，我们使用如下方法加载该包并显示包中的对象：

以上是该包中可用的4个函数名，通过阅读display.brewer.all()中的帮助信息可知，这是一个好的开始，因为这里列出了该包中所有可用的调色板。调用如下：

然后在Set3调色板中选择蓝色：

该颜色以十六进制格式存储，其中红色red为54，蓝色blue为27，绿色green为8F，它并没有包括α透明度，这意味着该颜色是不透明的。但是我们可以通过在Purples8的后面粘贴一个透明度值来生成该颜色的一个透明度版本：

我们将这个颜色作为散点图的绘制符号。
此外，我们通过在年龄上加一个分布在-0.5到0.5之间的随机数，来调整参赛选手的年龄。这个操作称为抖动（jittering），可以使用jitter(age, amount = 0.5)来抖动年龄的值。
图2-7中显示的是修改后的散点图。相比图2-6中的原始图，该图有了很大的改进。我们可以观察到大多数参赛选手在图中的位置，包括随着age的增加，run time轻微向上弯曲的现象，以及给定age的前提下，run time的一个倾斜分布。另外我们还可以看到有一小群参赛选手的跑步速度非常快。这里将这个散点图的绘制留作练习。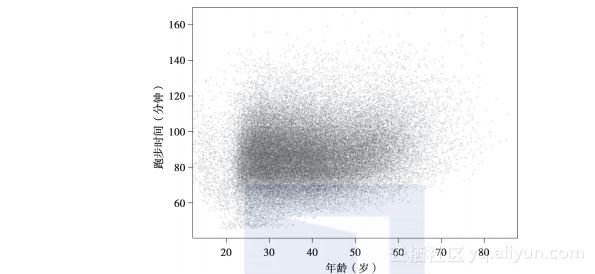

图2-7　修正后男选手的散点图。把图2-6中的绘制符号由圆圈变成了圆点，使用透明色，减少绘制符号的大小，并对年龄添加了少量的随机噪声。现在我们可以从图像中看到高密度区域包含大多数的参赛选手，并且跑步时间随着年龄的增长有轻微上升的趋势
smoothScatter()函数提供了一个对使用抖动和透明度更加规范的方法，用来可视化参赛选手的runtime-age密度分布。该函数使用颜色生成一个平滑的散点图密度表示，这一点和图2-7很类似，只是采用了更具统计性的方法来构建颜色浓度深浅变化的区域。通过smoothScatter()函数，在（x，y）处的颜色取决于这一点附近小区域内数据点的密度。这个平均化的过程使得在相应的高密度区域产生了一个平滑的深色阴影图。我们对cbMen调用函数smoothScatter()如下：

图2-8中显示的结果和图2-7中的绘图在形状上非常相似，只是图2-8中多了一些小黑点，表明一些单独的离群点远离了主体点云。
这些散点图的另一种非常不同的绘制方法是将参赛选手按大致相同的年龄段进行分组，以图示法显示各组选手跑步时间的统计概要。这里，我们把参赛选手以10年一个年龄段进行分组，并按箱线图的形式绘制每一小组的数据概要（见图2-9）。在这些并排的箱线图中，数据的多少并不会掩盖其主要特征，比如一个年龄组的四分位数和尾数。为了绘制这些箱线图，我们用cut()函数对年龄进行分类。首先移除15岁以下或拥有不切实际的跑步时间的选手，方法如下：

图2-8　男选手的跑步时间对年龄的平滑散点图。该图提供了不同于图2-7的另一种散点图绘制方法，图2-7中使用了抖动和透明色来解决过度重叠的问题。这里不需要对年龄进行抖动，因为平滑操作本身通过将单个参赛者的（age, runtime）分散到邻近的小区域而潜在地实现了抖动操作。图中的高密度区域和之前的散点图有着非常相似的形状
然后对年龄进行分类：

这个新变量ageCat，是一个因子，它把年龄以10年为一间隔进行分组，另外75岁以上的选手组成一组。
我们在如下的plot()调用中使用公式runtime~ageCat：

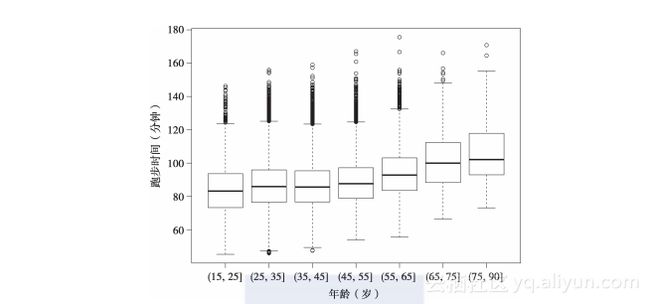
可以看到，在图2-9中plot()函数创建了一系列的箱线图而不是散点图。该函数调用与之前生成图2-6的函数调用之间的区别在于所提供的公式不同。由于ageCat是一个因子，对于公式time~ageCat，默认生成的是一系列并排的箱线图，而每个关于跑步时间的箱线图都由年龄因子中的一个分组决定。图中我们观察到上四分位数比中值和下四分位数随着年龄增长的速度更快。在下一节中，我们设法更正式地总结年龄和跑步时间之间的这种关系。
2.4.2　对平均成绩构建拟合模型
如图2-9所示，参赛选手的平均成绩似乎随着年龄的增长而向上弯曲，一个简单的线性模型可能不足以描述这种关系。首先我们来看简单线性模型捕捉这种跑步时间和年龄之间关系（或者没有关系）的能力如何。拟合模型如下：

图2-9　并排的男选手跑步时间相对年龄的箱线图。将男选手按年龄以10年为一间隔进行分组，箱线图按顺序显示了每组的四分位时间。所有的四分位值都随年龄的增长而增长，但是箱体随年龄的增长变得不对称，表示上四分位值比中四分位和下四分位值随年龄增长得更快
这里再次使用R公式语言来表达我们想要拟合的数据之间的关系。公式runTime~age表示我们想把跑步时间拟合为年龄的函数。Im()函数执行最小二乘法以寻找数据的最佳拟合直线，我们得到下面的截距和斜率：

我们已经指定从lm()向lmAge的返回值，该返回对象包含有关run time对age的线性最小二乘法拟合的系数、预测值、残差以及其他相关信息。我们可以调用summary()，得到关于拟合的一个简单概要：

注意summary()函数不会产生标准的分位数、极端值，等等。这是因为我们已经向它传递了一个lm对象，即

类lm的summary方法提供了一组不同的概要统计工具集，它更适合拟合线性模型。
为了有助于评估简单线性模型对数据的拟合程度，我们绘制残差关于年龄的图形。与原来的跑步时间关于年龄的散点图一样，我们需要解决数据过度重叠问题，在此我们使用smoothScatter()来进行处理。而且，为了能够看到残差的曲率，我们在绘图中添加了一条0水平线。使用的方法如下：

为了有助于进一步识别残差中的模式，我们用一条来自拟合残差的局部平均值的光滑曲线来增强该残差图形，也就是说，对某一特定的年龄，比如37岁，我们把那些年龄在37岁附近一个小邻域内选手的残差进行加权平均。这样的局部拟合曲线可以让我们更好地观察残差模式的偏离趋势。用loess()函数拟合该曲线如下：

注意loess()函数也接受一个公式对象来描述数据的拟合关系，这里我们想要的是resids关于age的拟合。由参数data提供的数据框中包含这两个变量；此外它还可以包含其他的变量，但是我们已经专门创建了这个数据框，使它只含有来自于ImAge的残差和cbMenSub中运动员的年龄。和Im()类似，loess()的返回值也是一个特殊对象，它包含被拟合的值和其他与数据拟合曲线有关的信息。
为了在残差的平滑散列中添加拟合曲线，我们可以预测每一年年龄的平均残差，然后用lines()在这些预测点之间直接“连接点”，形成一个近似的拟合曲线。我们先从在20～80之间生成一个年龄值向量开始：

现在如果在数据向量中对以上的每一个年龄调用被预测的平均残差，即调用resid.lo.pr，我们就可以把曲线添加到平滑散列中：

可以从predict.loess()函数中得到这些预测值，该函数从一个拟合和一个数据框中提取loess对象，例如，拟合为resid.lo，数据框由loess拟合曲线中需要匹配的变量组成，在本例中就是age。也就是说，我们通过如下方法创建resid.lo.pr：

注意，我们调用的是predict()，而不是predict.loess()。predict()函数是一个包装器，它允许我们不依赖于拟合的形式去编写代码。该函数接受一个从拟合函数中返回的对象，比如从lm()或loess()函数中返回对象，具体调用哪个拟合函数取决于对象所属的类。也就是，predict()自身会调用相关的函数，即对于Im对象调用predict.lm()，对于loess对象调用predict.loess()。
增强的平滑散点图如图2-10所示。我们看到，这个简单线性模型偏于低估超过60岁的男选手的跑步时间。这证实了我们在跑步时间呈非线性趋势的箱线图和平滑散点图上的观测：简单线性模型不能够捕捉选手成绩随年龄的变化。

图2-10　选手成绩关于年龄的简单线性拟合模型的残差图。这里显示的是一个平滑的残差散点图，表示的是15～80岁的男选手的跑步时间关于年龄的简单线性拟合模型的残差分布。在散点图上叠加了两条曲线，实线是y=0处的水平线，虚线是残差的局部平滑曲线
我们考虑两种更加复杂的拟合方法：分段线性模型和非参数平滑曲线。对于后者，我们仅取随年龄变化的局部加权平均时间，该方法与我们从线性拟合中平滑残差的方法类似。为此我们再次使用loess()函数：

并对20～80岁之间的所有年龄做预测：

曲线显示如图2-11所示。
接下来我们拟合分段线性模型，该曲线由几条线段连接而成。这类似于loess()函数局部平滑曲线的思想，局部平滑曲线允许我们在某些特定的点弯曲直线，以便更好地拟合数据。不同的是，分段线性模型的拐点之间的拟合必须是线性的。我们将拐点设置在30、40、50、60，并允许在这些十年标记点处改变直线的斜率。拟合“曲线”如图2-11所示。
如何让这样的模型拟合我们的数据呢？在拟合完整的分段模型之前，我们先考虑只有一个拐点在50岁的简单模型。首先创建over50变量，当年龄小于等于50岁时，over50取值为0，当年龄大于50岁时，over50的取值为年龄减去50的值。比如，51岁时取值为1，52岁时取值为2，依次类推。如果我们的拟合是a+b×age+c×over50，那么对于50岁以下的年龄，拟合简单表示为a+b×age，而对于50岁以上的年龄，拟合等于(a-50c)+(b+c)age。可以看到当年龄从低于50岁到高于50岁时，系数c表示斜率上的变化，而截距可以使线段进行连接。

图2-11　跑步时间关于年龄的分段线性拟合和Loess曲线。这里我们以30、40、50、60岁为拐点分别绘制分段线性拟合曲线和来自loess()的拟合曲线，这些曲线彼此接近。然而对于50岁以上的参赛选手来说，图中的loess拟合曲线比分段线性拟合曲线显示的曲率更大
那么我们第一个任务是创建over50变量。使用pmax()函数，执行逐个元素或“平行”的极大值算法。通过以下方法，我们可以得到menRes$age-50和0中的每一个元素的极大值：

然后我们拟合这个参数模型：

现在对于50岁以下的选手，直线的斜率比我们最初简单的线性模型更平缓，而对于年龄超过50岁的选手，该模型表明其平均用时比整体平均用时慢了0.67分钟，而整体平均用时又比50岁以下选手的平均用时多0.56分钟。
然后我们可以创建over30、over40等变量如下：

现在我们已经有了这些变量，下面便可以创建模型

这个模型与仅带有参数age和over50的模型有类似的解释。也就是，系数over40是年龄在（30，40]和（40，50]之间斜率上的变化。采用以下方法，得到最小二乘法拟合模型：

这里我们在公式中使用“.”表示这个模型应该包含数据框中作为协变量的变量（除了runTime之外）。
当我们以Im类的对象lmPiecewise作为参数，调用summary()函数时，我们会得到关于拟合的系数、标准差以及其他的概要统计数据:

注意，over60系数基本上为0，表明那些超过60岁的选手并不比他们50多岁的时候跑得慢多少。即年龄超过50岁的选手每增加一岁，跑步时间大概会增加0.404分钟，而10英里赛的所有选手每增加一岁，跑步时间大约平均增加0.66分钟。
我们如何绘制拟合出的分段线性函数呢？对于loess曲线，我们可以使用predict()函数，为20～80岁之间的每一个年龄值提供被拟合的值。分段线性函数的绘制与loess曲线的绘制相类似，不过需要为predict()提供全部的用于拟合的协变量，即age、over30、over40、over50和over60。我们可以创建一个包含这些协变量的数据框，就像我们对完整数据集创建数据框一样：

然后调用predict()函数进行预测，向predict()函数传递lm对象，即带有拟合细节信息的lmPiecewise；以及用于产生预测的协变量，即overAgeDF。也就是，我们调用predict()如下：

我们绘制拟合的分段线性函数如下：

然后添加loess曲线：

两个拟合曲线显示于图2-11。我们看到它们彼此非常接近。最主要的差别是在超过70岁的年龄组别。我们没有在70岁处添加拐点，以至于我们的模型无法捕捉到数据在年龄超过70岁后的剧烈增长。我们也许需要考虑在模型中增加额外的拐点以观察是否可以改善拟合的性能。看起来我们似乎已经在建模平均成绩上取得了很大的进步，但是我们必须小心解释这些结果。例如，假设，很可能那些跑得慢的年轻选手会随着年龄的增长退出比赛，这样那些参赛年龄较大的选手就将成为跑得更快的选手，而这会让我们在跑步速度如何随年龄变化的估计上产生偏差。此外，这些数据是由参赛选手的14个横截面快照组成的，我们可以问问自己，参赛选手的组成是否会随着参赛时间阶段的不同而发生变化呢？这些问题将是随后两节的主题。
2.4.3　横截面数据和协变量
在我们之前的分析中，考察了不同年龄段参赛选手的平均成绩。也就是，查看了在樱花赛中诸如30～39岁、40～49岁选手的平均成绩。但是，我们还没有看到选手的成绩如何随他或她的年龄增长而发生变化。这两个参赛组（30～39岁和40～49岁）分别由不同的选手组成。如果这两组选手的组成明显不同，例如，如果其中30多岁的选手很可能是世界级运动员，而40多岁的选手更可能是当地的业余运动员，那么如果只比较这两组选手的平均成绩，结果就可能被误导。我们有来自14个不同年份比赛的数据，为了进一步使问题复杂化，也将对这些不同年份比赛的选手数据进行交叉平均。我们预计这些年的平均水平是相同的，而每年都有一组自选组参赛选手，我们想知道每年自选组参赛选手的构成是否会发生变化。如果有，那我们可以进行进一步的复杂推断。
我们知道樱花10英里赛越来越受欢迎。图2-12表明男选手的参赛数量14年来增加了一倍多。看来提出在这段期间参赛选手的人员构成是否发生变化这一问题，似乎是合理的。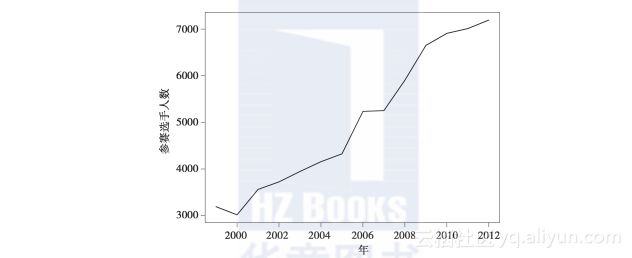

图2-12　逐年男选手参赛人数的曲线。该图表明1999～2012年，樱花10英里赛中男选手的参赛数量增加了一倍多
从历史上来看，樱花赛被当作波士顿马拉松赛的热身赛。在樱花赛中跑得最快的选手主要来自埃塞俄比亚、肯尼亚和坦桑尼亚，而且他们完成比赛的时间和2005年来自埃塞俄比亚32岁的选手Haile Gebrselassie创造的世界纪录44分24秒相差在1～2分钟之内（参见http://inglog.com/tools/world-records/）。说明有专业选手持续参加了樱花公路赛。
让我们比较一下最早的和最近年份参赛选手的成绩分布情况，即1999年和2012年的比赛。后面我们可以看到虽然2012年的最快成绩比1999年更快，但与1999年相比，2012年参赛选手成绩分布的每个四分位点都差不多要慢3分钟。

那么有没有可能2012年参赛者的年龄更大，因此比1999年同年龄段的选手跑得更慢呢？我们可以比较这两届比赛的年龄分布。
为简单起见，我们把1999年和2012年的选手年龄放入以下两个向量：

然后我们对这两个年龄集绘制叠加的密度曲线，操作如下：

注意第一次调用plot()绘图时，我们使用的是该函数缺省的水平和垂直坐标范围。当在第一个密度图中加入第二条密度曲线时，我们发现垂直轴没有大到能够包含第二条曲线的峰值。所以我们重绘了图形，指定ylim=c(0,0.05)，以容纳2012年密度曲线中较高的峰值。我们也可以使用lattice包[5]中的densityplot()函数，该函数可以根据所绘制的密度曲线恰当地自动缩放轴的大小。尽管如此，可视化处理通常是一个迭代的过程。我们在绘图时对大多数参数使用缺省设置，一旦发现有趣的结构，就重新绘制图形，以调整图形的比例并添加其他的信息，例如，轴的标签、标题、图例、颜色、线的类型和粗细等。
图2-13中的密度曲线令人惊讶，2012年的男选手年龄并不大。事实上，情况正好相反，与1999年相比，2012年有更多的年轻选手，可以证明这一点的是2012年的年龄分布图中在大约30岁处有一个尖锐的峰值。我们也可以绘制一个分位点对分位点的图来比较这两个分布，这里把它留作练习。与参赛选手年龄的老化程度相比，1999年和2012年选手的成绩相差会更小一些。在分析比赛成绩时，我们需要同时控制协变量、年龄和年份。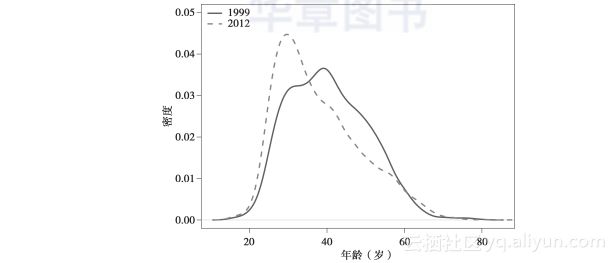

图2-13　1999年和2012年男选手的年龄密度曲线。这两条密度曲线的形状相差很大。1999年的男选手的年龄分布模式宽阔且近乎平坦，在28～45岁之间大致呈均匀分布。相比之下，2012年的参赛选手更年轻，在30岁处有一个尖峰，呈右偏斜分布
在之前的章节我们看到，参赛选手的平均成绩在30多岁时很平坦，在40多岁时有小幅上涨，而在50多岁和60多岁时上涨得更快。针对1999年和2012年的参赛选手，我们分别绘制其“年龄-时间”的平滑曲线，并把两条曲线绘制在一张图上，如图2-14所示。

从图2-14中我们看到两条曲线的形状相似，但是2012年的曲线高于1999年的曲线，表明在两组参赛选手之间存在着一致性差异。图2-15显示了这两条曲线在预计跑步时间上的这种差异。在50多岁时两者的差距最小到2分钟，从60多岁、70多岁到80多岁，差距逐渐从2.5分钟增加到8.5分钟。这里我们把比较所有14年数据中跑步时间和年龄之间关系的任务留作练习。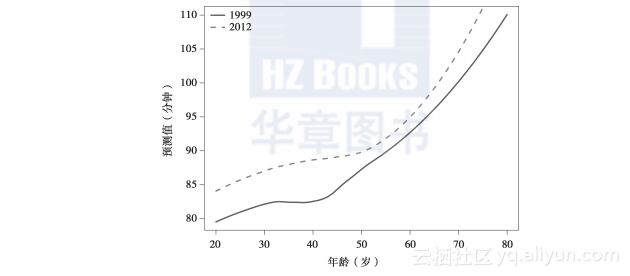

图2-14　1999年和2012年男选手成绩的loess曲线拟合。2012年男选手的“成绩-年龄”loess拟合曲线位于1999年曲线的上方。在多数年龄上这两条曲线之间相差大约5分钟，而在40多岁的后期到60多岁的前期两条曲线彼此相差2～3分钟。这两条曲线的形状相似
现在我们来看比较两组选手分布的最后一个想法，并将该比较工作留作练习。在该过程中，存在一个被称为年龄组别的成绩标准，可以根据他或她的年龄来衡量其个人的成绩。该方法根据个人所在年龄分组相同距离上的世界纪录来标准化他的跑步时间[1]。由于樱花公路赛中跑得最快的选手的成绩接近于世界纪录，因此我们可以用每个年龄段中的最快时间来标准化该组选手的时间。为了最小化年度之间的波动，我们将最快时间进行平滑处理，然后用平滑的最快时间来标准化每个选手的时间。这样做时，我们发现各年龄组别的成绩大致服从正态分布。不过，1999年的选手成绩同比好于2012年，能证明这一点的是1999年的峰值出现在1.4而不是1.5，且具有更小的IQR值。
跑步时间的分布似乎逐年在变化，这就引出关于横截面研究这一主要问题。不过，对于该研究，我们有14年的跑步结果数据这一优势。很可能一些参赛选手参加过多年的比赛，这样我们就可以研究随着他或她年龄的增长，比赛成绩随之变化的情况。为了得到这个结果，我们需要把参赛选手的跨年度数据关联起来。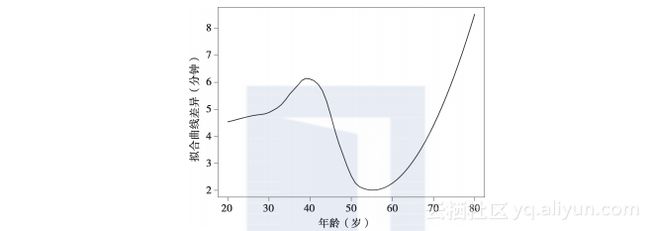

图2-15　Loess曲线差异。这条线显示了被预测的2012年和1999年男选手的跑步时间之间的差异