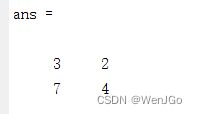数模学习02-Matlab基础知识入门
先把matlab下载好。然后你就会发现电脑有少了几十个GB。服啦~
修改字体
字体真的是太小了,其实我无论是使用什么编辑器我一般都会先改字体,字体在开始中有一个预设,可以修改字体,这样眼睛看着也会舒服一点
命令行窗口的使用
这里可以直接在命令行窗口输入某些命令。
例如 10*9 = 90
他会自动的返回一个answer给你
工作区显示变量
在使用命令行窗口操作一些数据之后可以在工作区找到对应的值
Matlab基本知识
1.基本的操作
(1)分号
在每一行的语句后面加上分号(一定要是英文的" ; "):表示不显示运行结果
但是即使没有显示,在工作区还是可以体现。
一般中间计算的结果都是需要添加分号的。
分号同时也可以作为区分行的标志
(2)注释
标准格式为 在你要注释的代码前添加 %即可
快捷键 Ctrl+R
取消注释 Ctrl+T
(3)清除工作区clear
clear可以清楚工作区的所有变量
我现在的工作区
在输入clear之后,工作区就全部清空了
(4)清除命令行窗口内容
clc可以清除命令行窗口中的所有文本,让屏幕变得干净
所以经常一起使用 clear;clc
这两条一起使用,起到“初始化”的作用,防止之前的结果对新脚其他程序文件产生干扰。
2.常用的操作函数
(1)输出和输入函数(disp 和 input)
disp:是屏幕输出函数,类似于c语言中的printf()函数
在matlab中,字符串可以使用单引号或者双引号都可以
例如:
disp('单引号')
disp("双引号")
运行结果
接下来还可以输出向量
比如
%行向量:同一行中间可以用逗号分隔,也可以用空格
a = [1,2,3]
a = [1 2 3]disp(a)
% 列向量使用 “;”来隔开
b = [3;4;5]
disp(b)
这在里disp,后面加不加分号都会有运行结果,不然这个函数加了;没用了那她还有什么用。
(2)字符串的合并
matlab中两个字符串的合并有两种方法
[1]方法一:使用strcat(str1,str2……,strn)
strcat('字符串1','字符串2')
示例代码如下:
[2]方法二:[str 1,str 2,……, str n]或[str1 str2 …… strn]看成一个行向量
['祖国的','大好河山',"我想去看看"]
注意,第一种方法确实可以 ' 和 " (单引号和双引号)混用,但是第二种就不可以了
(3)数字转换为字符串
num2str: 将数字转换为字符串
c = 100
num2str(c)% 那么以后就可以拼接数字类型了
disp(['c的取值为' num2str(c)])
disp(strcat('c的取值为', num2str(c)))
结果示例
如果这里直接将c放在字符串后面的话。会自动将c的数字类型通过ANSIC码转换为对应的字符串然后再拼接,最后输出结果。
(4)input函数
input:将输入的数、向量、矩阵、字符串等赋给一个变量
这里和Python很相似,在input中的字符串是一个提示
A = input('请输入A:');
B = input('请输入B:')
不加分号的话,不会输出,但是会在工作区展示
(5)sum函数
【1】如果是向量(无论是行向量还是列向量),都是直接求和
E = [1,2,3]
sum(E)
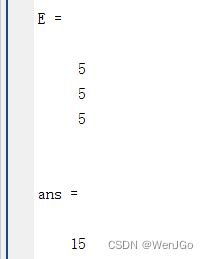
E = [1;2;3]
sum(E)
【2】如果是矩阵,则需要根据行和列的方向作区分
sum后面的第二个参数可以指定对应的数字,如果不写
默认是 1 :按列求和(得到行向量),如果指定为2就是按行求和(得到列向量)。
E = [1,2;3,4;5,6] % 三行二列的矩阵
% a=sum(x);% 按列求和(得到一个行向量)
a = sum(E)
% a=sum(x,2); %按行求和(得到一个列向量)
a = sum(E,2)
% a=sum(x(:));%对整个矩阵求和
a = sum(sum(E))% E(:) 一列一列的将全部列拼接为一列
E(:)
a = sum(E(:))
(6)提取矩阵中的指定元素
先定义一个矩阵
A=[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1];
A
【1】取指定元素:第一个参数是行号,第二个参数是列号,都是从1 开始
A(2,1)
A(3,2)
【2】取指定某一行全部元素:取指定的某一行的全部元素(输出的是一个行向量)
A
A(2,:)
A(5,:)
【3】取指定某一列全部元素:: 取指定的某一列的全部元素(输出的是一个列向量)
A
A(:,1)
A(:,3)
【4】取指定的某些行的全部元素:输出的是一个矩阵
A
A([2,5],:) % 只取第二行和第五行(一共2行)
A(2:5,:) % 取第二行到第五行(一共4行)
A(2:2:5,:) % 取第二行和第四行 (从2开始,每次递增2个单位,到5结束)
1:3:10 % 1 4 7 10
10:-1:1 % 10 9 8 7 6 5 4 3 2 1
A(2:end,:) % 取第二行到最后一行
A(2:end-1,:) % 取第二行到倒数第二行
运行结果:
A =1.0000 1.0000 4.0000 0.3333 3.0000
1.0000 1.0000 4.0000 0.3333 3.0000
0.2500 0.2500 1.0000 0.3333 0.5000
3.0000 3.0000 3.0000 1.0000 3.0000
0.3333 0.3333 2.0000 0.3333 1.0000
ans =1.0000 1.0000 4.0000 0.3333 3.0000
0.3333 0.3333 2.0000 0.3333 1.0000
ans =1.0000 1.0000 4.0000 0.3333 3.0000
0.2500 0.2500 1.0000 0.3333 0.5000
3.0000 3.0000 3.0000 1.0000 3.0000
0.3333 0.3333 2.0000 0.3333 1.0000
ans =1.0000 1.0000 4.0000 0.3333 3.0000
3.0000 3.0000 3.0000 1.0000 3.0000
ans =1 4 7 10
ans =10 9 8 7 6 5 4 3 2 1
ans =1.0000 1.0000 4.0000 0.3333 3.0000
0.2500 0.2500 1.0000 0.3333 0.5000
3.0000 3.0000 3.0000 1.0000 3.0000
0.3333 0.3333 2.0000 0.3333 1.0000
ans =1.0000 1.0000 4.0000 0.3333 3.0000
0.2500 0.2500 1.0000 0.3333 0.5000
3.0000 3.0000 3.0000 1.0000 3.0000>>
【5】取全部元素:按列拼接的,最终输出的是一个列向量
A
A(:)
(7)size函数
size(A):函数是用来求矩阵A的大小的,它返回一个行向量,第一个元素是矩阵的行数,第二个元素是矩阵的列数
A = [1,2,3;4,5,6]
B = [1,2,3,4,5,6]
size(A)
size(B)
% 将矩阵A的行数返回到第一个变量r,将矩阵的列数返回到第二个变量c
r = size(A,1) %返回行数
c = size(A,2) %返回列数
(8)repmat函数
B = repmat(A,m,n): 将矩阵A复制m×n块,即把A作为B的元素,B由m×n个A平铺而成。
m*n也可以理解为,将A铺为m行,n列
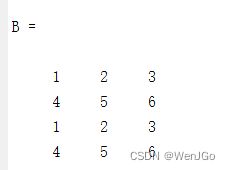
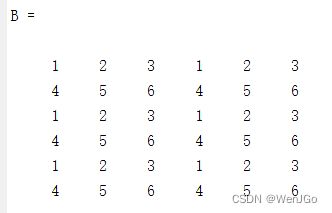
A = [1,2,3;4,5,6]
B = repmat(A,2,1)
3.Matlab中矩阵的运算
(1)矩阵乘法 *
先了解一下矩阵的乘法的操作过程
MATLAB在矩阵的运算中, “ * ” 号和 “ / ” 号代表矩阵之间的乘法与除法
A = [1,2;3,4]
B = [1,0;1,1]
A * B
-----------------------------------------
两个形状相同的矩阵对应元素(不是真正的乘除法是每个元素之间的操作,每个位置上的元素独立操作)之间的乘除法需要使用 “ .* ” 和 “ ./ ”
A = [1,2;3,4]
B = [1,0;1,1]
A .* B
A ./ B
运行结果如下:
A =1 2
3 4
B =1 0
1 1
ans =1 0
3 4
ans =1 Inf
3 4
-----------------------------------------
每个元素同时和常数相乘或相除操作上面的两种操作方法都可以
所以这里的点乘和乘,点除和除都是一个相同效果
A = [1,2;3,4]
A * 2
A .* 2
A / 2
A ./ 2
-----------------------------------------
每个元素同时乘方时只能用 .^ 如果使用的是 ^ 那就是两个矩阵相乘
A = [1,2;3,4]
A .^ 2
A ^ 2 == A * A
A * A
运行结果如下
A =1 2
3 4
B =1 0
1 1
ans =1 0
3 4
ans =1 Inf
3 4>> A = [1,2;3,4]
A * 2
A .* 2
A / 2
A ./ 2A =
1 2
3 4
ans =2 4
6 8
ans =2 4
6 8
ans =0.5000 1.0000
1.5000 2.0000
ans =0.5000 1.0000
1.5000 2.0000>> A = [1,2;3,4]
A .^ 2
A ^ 2
A * AA =
1 2
3 4
ans =1 4
9 16
ans =7 10
15 22
ans =7 10
15 22>>
(2)求矩阵的逆矩阵 inv(矩阵)
A/B = A*inv(B)
求B的逆矩阵
B = [1,0;1,1]
// 利用原矩阵乘以它的逆矩阵得到单位矩阵即可验算
B * inv(B)
A * inv(B)
A / B
(3)Matlab中求特征值和特征向量
// 在Matlab中,计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法:
A = [1 2 3 ;2 2 1;2 0 3]
// E=eig(A):求矩阵A的全部特征值,构成向量E。
E=eig(A)
// [V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。(V的每一列都是D中与之相同列的特征值的特征向量)
[V,D]=eig(A)
运行结果如下:
A =1 2 3
2 2 1
2 0 3
E =-1.3166
5.3166
2.0000每一列都是一个特征向量
V =0.8364 -0.6336 -0.2408
-0.3875 -0.5470 -0.8427
-0.3875 -0.5470 0.4815
D =-1.3166 0 0
0 5.3166 0
0 0 2.0000V和D的特征值和特征向量是对应的
也就是说,D是第几列,它的特征向量就在V的第几列
(4)find函数的基本用法
Matlab在存储矩阵时,是一列一列存储的
// find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
返回的是 *索引*
X = [1 0 4 -3 0 0 0 8 6]
ind = find(X)
// 其有多种用法,比如返回 前2个不为0的元素 的位置:
ind = find(X,2)// 上面针对的是向量(一维),若X是一个矩阵(二维,有行和列),索引该如何返回呢?
X = [1 -3 0;0 0 8;4 0 6]
// 这是因为在Matlab在存储矩阵时,是一列一列存储的,也就是将它优化成了一列我们可以做一下验证:
X(4)// 这里的r和c就是代表每次找到的这个元素在第几行或者第几列
[r,c] = find(X)
[r,c] = find(X,1) %只找第一个非0元素
4.矩阵与常数的大小判断运算
共有三种运算符:大于 > ;小于 < ;等于 == (一个等号表示赋值;两个等号表示判断和编程是一样的)
X = [1 -3 0;0 0 8;4 0 6]
X > 0
X == 4
运算结果如下:
logical 数组(逻辑数组)
0代表否 , 1代表是
这里输出的数组为0就代表false,是1就代表true即当前元素经过判断后成立
>> X = [1 -3 0;0 0 8;4 0 6]
X =
1 -3 0
0 0 8
4 0 6>> X > 0
ans =
3×3 logical 数组(逻辑数组)
1 0 0
0 0 1
1 0 1>> X == 4
ans =
3×3 logical 数组
0 0 0
0 0 0
1 0 0
5.判断语句
Matlab的判断语句,if所在的行不需要冒号,语句的最后一定要以end结尾 ;
中间的语句要注意缩进。
a = input('请输入考试分数:')
if a >= 85
disp('成绩优秀')
elseif a >= 60
disp('成绩合格')
else
disp('成绩挂科')
end
运行实例:
结语
结束下一篇文章会更新层次分析法的代码的写法。
ヾ( ̄▽ ̄)Bye~Bye~