机器学习理论之(4):模型评估方法,如何评价分类器,如何切分数据集,错误类型,二分类的混淆矩阵,多分类混淆矩阵,baseline & benchmark
文章目录
- 选择测试数据
-
- 优秀分类器指标
- 衡量分类器性能的一般方法
-
- Question
- 切分训练测试集(Train / test split )
-
- Questions:
- 简单随机划分(random handout)
- 留一法(leave-one-out)
- 留一法交叉验证(leave-one-out cross validation)
- 重复随机分段采样(repeated random subsampling)
- K-折交叉验证(K-fold cross validation)
- 现实问题
- 解决方案:分层(垂直)采样
- Question
- 归纳学习假说(Inductive learning hypothesis)和 归纳偏差(inductive bias)
- 验证集(validation set)
- 评估方法(evaluation methods)
-
- 评估指标(evaluation metrics)
- positive v.s. negative 样本
- TP, FP, FN, TN
- 正确率和错误率(Accuracy & error rate)
- 错误降低率(error rate reduction)
- Question
- Precision & Recall
- Sensitivity & specificity
- 多分类模型评估(Multiclass evaluation)
-
- one-v.s.-rest
- Macro-averaging
- weighted averaging
- 模型对比:baselines & benchmarks
-
- baseline 举例
选择测试数据
优秀分类器指标
- 我们训练优秀的分类器,本质上是训练一个泛化性强的模型,这个模型不能只是见一个认识一个,必须要能够面对没见过的样本做出尽可能准确的预测才行
- 我们训练和使用的这个模型,其实本质上就是一个函数 f ( x ) f(x) f(x),对于分类任务来说,我们对于这个训练好的 f ( x ) f(x) f(x),给定一个输入样本,它会输出一个预测的结果(predicted label),即 f ( x ) = y ^ f(x) = \hat{y} f(x)=y^
- 而我们真实的这个样本的标签我们用 y y y 来表示。很显然当你拿到 y ^ \hat{y} y^ 的时候,你就能够判断它是不是和这个样本的标签是一致的,通过测试集中所有的样本输入这个模型,就可以得到所有测试集的 y ^ \hat{y} y^ 从而也就可以统计出这个模型的准确率(accuracy)。
衡量分类器性能的一般方法
- 通常来说我们会简单地使用精确度 accuracy 来表征一个分类器性能的好坏:
a c c u r a c y = n u m b e r o f c o r r e c t l a b e l e d t e s t i n s t a n c e s t o t a l n u m b e r o f t e s t i n s t a n c e s accuracy = \frac{number ~of ~correct ~ labeled~ test ~ instances}{total~number~of ~test~instances} accuracy=total number of test instancesnumber of correct labeled test instances
- 在很多情况下,这是适用的,但是我们在下面的内容将不仅仅局限于此,本文会给出一些场景,帮助你理解,为什么很多时候 accuracy 的评价指标是远远不够的。
Question
-
思考在下面的场景下,accuracy 的衡量标准是否会失效:
- 我们现在使用 100 个样本,患癌症的人 label=1, 不患癌症的 label=0 ;假设人群中有 1% 的人罹患癌症,现在构建了一个模型,预测一个人会不会得癌症,这个模型没有经过任意训练,它也只能输出一个结果,就是 0。
- 那么此时用 accuracy 来衡量这个模型的精度是完全没有意义的。因为就算它没有任何训练,由于癌症病人的存在概率非常低,所以这个模型的精度会轻松达到 90% 以上甚至更高。
-
思考下面的场景,描述的是正确的还是错误的?
- 如果两个模型在同一个测试集上拥有相同的 accuracy,是否代表他们学到了同样程度的信息?
- 如果两个模型在同一个测试集上有相同的错误模式(即判错的样本是完全重合的)他们是否学到了同样程度的信息?
- 一个模型在一个测试集上比另外一个模型高,是否就代表在另一个测试集上也会同样比另外一个模型高?
-
答案当然都是否定的:
- 对于第一个问题,一方面测试集只有一个,相同的 accuracy 并不能够代表他们学习的程度是一样的;另外一方面,即使他们学习的程度各有不同,也有可能得到相同的 accuracy
- 第二个问题,即使一些样本对这两个模型来说都是困难的样本,那也不代表这些困难样本让这两个模型分类错误的原因是相同的,可能第一个模型是因为一部分特征没有学习好而分错,第二个模型因为另外一部分特征没有学习好而分错
- 第三个问题则更加错误,因为一个测试集上的结果好,一方面可能这个测试集的样本更加有利于第一个模型的学习结果,也有可能第一个模型在某些情况下效果特别好,甚至存在过拟合的情况,那么这个时候如果换一个数据集,其结果未必就比第二个好
-
那么如何选择合适的数据来进行训练和测试呢?
切分训练测试集(Train / test split )
- 让分类器在训练集上(training set)训练,在测试集(testing set)上测试
- 那么如何科学的划分训练和测试集呢?
Questions:
为什么不把数据全部用来训练:
- 如果你不划分出来测试集,你就没有办法对模型的精度进行验证,也同样无法通过参数调整来让模型有更好的表现
为什么不能用训练的数据来测试
- 因为训练过程中模型已经见过训练样本,如果测试数据中包含了训练样本,相当于一种 “cheating” 欺骗和作弊行为,会让模型的精度提高,但其实掩盖了其真正的精度;
- 因此在测试集中绝对不能出现用来训练的样本
简单随机划分(random handout)
- 最简单的方法来划分:
- 训练集 / 测试集 = 50%:50% 或 80%:20% 或 90%:10%
- 将训练集和测试集按照这个比例进行随机划分,训练一个模型
留一法(leave-one-out)
- 顾名思义:只留 1 1 1 个样本用来测试,将数据集中的其他所有样本用来训练
留一法交叉验证(leave-one-out cross validation)
- 通常用在数据量比较小的情况下
- 假设数据集中一共有 N N N 个样本,那么将一个样本作为测试集将剩下的样本全部作为训练集,训练一个模型,在选择另一个样本作为测试集,其他所有样本作为训练集再训练另外一个模型,如此重复,直到整个数据集中所有的数据都完成这个过程;
- 这个过程中一共会生成 N N N 个模型,每个模型都被 N − 1 N-1 N−1 个训练样本和 1 1 1 个测试样本训练和测试过;
- 将这 N N N 个模型的精度进行取平均运算,得到的结果就是最终的精度结果
- 因为当数据量本来就很小的时候,留出过多的样本测试会导致训练样本缺乏而训练不充分;而且只有数据量小的情况下才能支撑复杂度这么高的运算
重复随机分段采样(repeated random subsampling)
- 假设一个数据集样本 100 100 100 个,从样本集合中随机采样出 60 % 60\% 60% 用作训练,另外 40 % 40\% 40% 用作测试,训练一个模型。将这个过程重复 m m m 次,最终得到了 m m m 个模型,这 m m m 个模型的精度均值作为模型的最终精度。
- 但是这样存在的问题就是:
- 由于是多次随机采样,所以有部分样本可能在训练这个 m 个模型的过程中都被采样到了,而也有可能很多样本在这 m 次的采样过程中都没有用到。这样就会导致训练样本没有完全充分地利用
- 相对于一次性随机划分(random handout)的方法,这种方法也更可靠,但是计算量不免要大很多,因为要进行多次划分和多个模型的训练
K-折交叉验证(K-fold cross validation)
- 将数据集均等划分成 K K K 份,第 1 1 1 份作为验证集,剩下 K − 1 K-1 K−1 份作为训练集,得到第一个模型 M 1 M_1 M1 ;同样的方法,将这个 K K K 份中的第 2 2 2 份作为验证集,剩下 K − 1 K-1 K−1 份作为训练集,训练第二个模型 M 2 M_2 M2, 如此重复,一共训练 K K K 个模型,而所有的样本也都充分利用了。
- K K K 一般选择 5 5 5 或者 10 10 10;因为太大了对训练很不友好,训练过程太耗时
现实问题
- 我们是否应该保持训练集和测试集中的样本类别分布是相同的?
- 训练和测试数据中的各个类别的样本比例不一样,比如猫狗分类的数据集如果训练集里面有 80 % 80\% 80% 是猫的样本, 20 % 20\% 20% 是狗的样本而测试集中 80 % 80\% 80% 是狗的样, 20 % 20\% 20% 猫的样本
- 这样就很麻烦,因为这样训练出来的模型在训练集上表现会很差
解决方案:分层(垂直)采样
- 让训练和测试集上的数据具有相同的分布。相同的分布的意思就是:每个类占总样本的比例是一样的。
- 这篇文章中的例子讲的很好,简而言之:
- 我们想研究大学生的某些行为,现在假设全国有 21000000 学生,我们不可能对这 21000000 个学生进行全部研究,所以我们需要采样一部分样本来代替总体,假设我们抽取 4000 个人来进行研究,假设我们随机抽取的情况如下:
- 560名英语专业学生,1135名理科专业学生,800名计算机专业学生,1090名工科专业学生,415名数学专业学生
- 但是通过对这 21000000 学生进行统计后发现,他们中间的分布情况应该是:
- 主修英语的学生占12%,主修科学的学生占28%,主修计算机科学的学生占24%,主修工程的学生占21%,主修数学的学生占15%。
- 因此,为了让 4000 个样本可以代替 21000000 人,我们必须保证随机抽取的 4000 个人中各个学科学生的比例也是:英语的学生占12%,主修科学的学生占28%,主修计算机科学的学生占24%,主修工程的学生占21%,主修数学的学生占15%;
- 所以我们最终采样的时候,应该是随机挑选 选择英语480名,理科1120名,计算机960名,工科840名,数学600名 来组成这个 4000 人的数据集
- 我们想研究大学生的某些行为,现在假设全国有 21000000 学生,我们不可能对这 21000000 个学生进行全部研究,所以我们需要采样一部分样本来代替总体,假设我们抽取 4000 个人来进行研究,假设我们随机抽取的情况如下:
- 上面这个过程就是一个分层采样的过程,我们按照学科一共采样了 5 个不同的层(类)的学生
参考文章:
https://www.investopedia.com/terms/stratified_random_sampling.asp
Question
-
为了建设智慧城市,假设现在要训练一个模型来识别道路上的行人,从墨尔本的交通系统中选取了 5 天的行驶记录共 3000000 条数据作为训练集。
-
请问如果将视频中的奇数帧作为训练集,偶数帧作为测试集,合理么?
-
答案当然是不合理,两个连续的帧之间的信息几乎是完全一样的,这是前面提到的 cheating 行为,并没有检测出模型的泛化性

归纳学习假说(Inductive learning hypothesis)和 归纳偏差(inductive bias)
- 当一个模型经过大量的数据训练后,会对没有见过的样本依然存在泛化性
- 然而,一个模型的好坏并不能完全决定于数据量的大小,因为如果模型的假设是错误的,大量的数据训练之后,决定只能是更加错误的。
- 举个简单的例子,如果我们的数据样本由 100 个 attributes 组成,这 100 个 attributes 都是相互独立的,那么在这种情况下我们采用朴素贝叶斯再加上大量的数据支持,最后的预测结果就会非常好,因为朴素贝叶斯的一个很强的条件假设就是:各个 attributes 之间是相互独立的。但如果这些 attributes 之间的关联性是比较强的,朴素贝叶斯的假设就与数据本身存在不可调和的根本性问题,这个时候即使用很大量的数据进行训练,最终的结果也会很不好。
- 这一类由于假设错误而导致结果不好的问题我们称为 “inductive bias”归纳偏差
- 因此对于不同的问题和场景,我们应该选择最合适的假设来构建模型
验证集(validation set)
- 有些时候,我们不仅需要把数据集切分成训练集和测试集,我们还需要额外切分一个验证集
- 验证集可以简单地看做是:训练集的测试集,因为在训练的过程中我们需要根据训练过的阶段性模型在验证机上的精度表现来实时调整模型的参数和超参数从而获得更好的结果或者模型是否收敛
- 在很多情况下,我们也会不区分验证集和测试集
评估方法(evaluation methods)
评估指标(evaluation metrics)
- 前面提到的 accuracy 是我们常用的一个衡量模型优劣的重要指标
- 但我们前面也提到了,这个指标在很多情境下是不足以表征模型水平的,下面我们详细讨论
- 在下面的例子中我们将会采用上面提到的检测行人的案例来做进一步探究
positive v.s. negative 样本
- 在二分类问题中,我们通常区分正样本和负样本。
- 假设我们要让我们的模型区分一张图片是 “猫”还是“非猫”,我们不仅要给所有数据中的 猫 label=1,我们还需要给那些 “非猫”的样本 label=0;
- 这个道理其实很简单,想让模型理解什么是 “猫”首先就要告诉他,哪些特征是 “非猫”,因此任何一个分类问题,一定都存在正样本和负样本,在这个猫和非猫的分类问题中,那些 label=1 的图片就是正样本(positive),label=0 的图片就是负样本(negative)
TP, FP, FN, TN
- 知道了样本分为 postive 和 negative,我们就可以详细地定义每一种错误的类型,假设在当前二分类的情境下我们规定 label=1 是正样本, label=0 是负样本:
- 当一个样本自身 label=1,同时模型预测的结果 l a b e l ^ \hat{label} label^ 也是 1 那么这个时候就是一个 truePositive;true 代表预测的结果和真实的结果一致,Positive 代表模型 predict 的结果是个 positive
- 当一个样本自身 label=0,同时模型预测的结果 l a b e l ^ \hat{label} label^ 也是 0 那么这个时候就是一个 trueNegative;true 代表预测的结果和真实的结果一致,Negative 代表模型 predict 的结果是个 Negative
- 当一个样本自身 label=1,同时模型预测的结果 l a b e l ^ \hat{label} label^ 是 0 那么这个时候就是一个 falseNegative;false 代表预测的结果和真实的结果不一致,Negative 代表模型 predict 的结果是个 Negative
- 当一个样本自身 label=0,同时模型预测的结果 l a b e l ^ \hat{label} label^ 是 1 那么这个时候就是一个 falsePositive;false 代表预测的结果和真实的结果不一致,Positive 代表模型 predict 的结果是个 positive
正确率和错误率(Accuracy & error rate)
- 正确率是所有 ture 的情况除以样本总数(当 lable 和 l a b e l ^ \hat{label} label^ 一致的情况就算模型判断正确)
- 错误率是所有 false 的情况除以样本总数(当 lable 和 l a b e l ^ \hat{label} label^ 不一致的情况就算模型判断错误)
错误降低率(error rate reduction)
-
这是一个用于模型比较的概念和评估指标
-
例如对数据集 D, 对这个数据集采用了两个模型进行训练和精度测试,A 模型错误率 55 % 55\% 55%,B 模型错误率 32 % 32\% 32%
-
所以降低了: ( 55 − 32 ) 55 = 41.8 % \frac{(55 - 32)}{55} = 41.8\% 55(55−32)=41.8%
-
如果 error rate reduction > 0 代表现在的模型优于原来的模型,反之则证明现在的模型比原来的模型更差
Question
不同的错误率之间的重要程度是相同的么?
- 当然不是
- 在行人识别的例子中,假设行人是正样本 label=1,非行人(汽车、房屋、路灯等)的label都=0,那么这个时候我们来分析一下各种不同的错误造成的影响:
- falsePositive:明明是一个非行人,却 predict 成了行人,这个问题不严重,对模型来说最多是一次误判,增加了模型的 loss
- falseNegative:明明是一个行人,却判断成了非行人,这个问题特别严重。在实际应用中,这种问题出现的时候,汽车会因为预测错误而造成交通事故
- 因此在这个问题的情境中,falseNegative 要严重一些,我们更需要关注哪些 falseNegative 情况所占的比例,从而避免这类事情的发生
再让我们看一个例子:
-
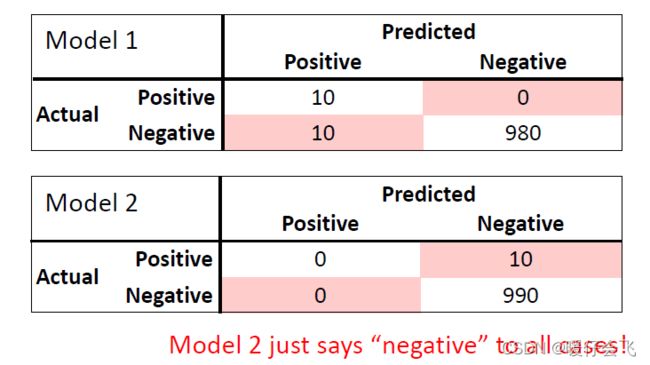
我们已经开发了两种机器学习方法来检测疾病。 我们在 1000 1000 1000 个病例中测试了每种算法(其中 1 % 1\% 1%的患者患有这种疾病)。 每个模型的准确率都是 99 % 99\% 99%。
-
第二个模型虽然正确率也是 99 % 99\% 99% 但是他只要对每个人都预测其 l a b e l ^ = 0 \hat{label}=0 label^=0 它的精确度就已经可以非常高了,因为这个并在人群中本就发病率很低
-
在这种情况下讨论 accuracy 就没有意义了,因为更重要的是他能不能把那些真正有病的人筛选出来
Precision & Recall
-
Precision 衡量的是:在所有的正样本中(真正 label=1 的样本和预测的 l a b e l ^ = 1 \hat{label}=1 label^=1 的样本)有多少样本是真真正正的 l a b e l = 1 label=1 label=1
-
Recall 衡量的是:在所有真正 l a b e l = 1 label=1 label=1 的样本中,有多少是模型真正判断出来的
-
- Precision 用的是一列计算
- Recall 用的是一行计算
-
在理想情况下,我们希望 precision 和 recall 都越接近 1 越好
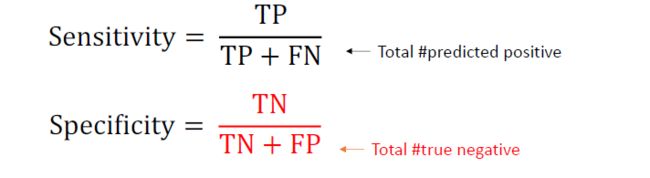
Sensitivity & specificity
多分类模型评估(Multiclass evaluation)
one-v.s.-rest
- 上文中我们把这个表格叫做混淆矩阵(cofusion matric)
- 我们之所以能够画出这个 2 × 2 2×2 2×2 的矩阵,是因为我们把一类看做是 positive 样本,一类是 negative 样本
- 那对于多分类的情况下,我们怎么来构成这个混淆矩阵呢?
- 在这个多分类任务的图表中,我们容易得出结论,那就是这个表格对角线上的值都是他们的 truepositive 的情况;那其他三种状态的样本跑到哪里了呢?
-
其实当我们面对多分类的情况,我们只要把其中的一类看做是 positive (label=1)样本,其他的所有类都看作 negative (label=0)样本,就可以得出混淆矩阵了。
-
结合上图来看:
-
我们上面已经以 pedestrian 为 positive 求算了它的混淆矩阵;
-
接下来我们可以以同样的方法求算所有类的混淆矩阵,并求出每个类的 precision,recall
-
然后我们将每个类的 precision 和 recall 进行求平均,即可得到整个多分类模型的指标
Macro-averaging
- 其中 c c c 代表了所有的 classes , i i i 是第 i i i 个 class
weighted averaging
- 不同类的样本可能会存在不均衡的情况,因此我们采用加权平均的方式,阳光本量大的类别,我们就在计算整体 precision 和 recall 的时候给与更多的权重
模型对比:baselines & benchmarks
- baseline 就是:给定一个数据集,选定一个模型,对这个数据集做出预测,这个模型的精度我们可以作为一个基准,并用此来衡量我们自己提出的模型,比较他们之间的各项指标
- benchmark:对于给定的数据集,当前业界比较好的模型在这个数据集上的各项表现
- 很多时候我们并不会特别地区分 baseline 和 benchmark
- 因为你可以选择任意一个模型作为基准,因此很多时候 benchmark 就可以当做 baseline



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MeZs43Dh-1647540213465)(attachment:image.png)]](http://img.e-com-net.com/image/info8/5fe8f5f402e04ccbb57f75a0ce2aa227.jpg)


![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mOnIXrrU-1647540213468)(attachment:image.png)]](http://img.e-com-net.com/image/info8/c4a92ef51fc54ab6beafee9850d77b96.jpg)