七大查找之哈希查找

1.基本思想

哈希查找算法又称散列查找算法，是一种借助哈希表（散列表）查找目标元素的方法，查找效率最高时对应的时间复杂度为 O(1)。

哈希查找算法适用于大多数场景，既支持在有序序列中查找目标元素，也支持在无序序列中查找目标元素。讲解哈希查找算法之前，我们首先要搞清楚什么是哈希表。

哈希表（Hash table）又称散列表，是一种存储结构，通常用来存储多个元素。

和其它存储结构（线性表、树等）相比，哈希表查找目标元素的效率非常高。

每个存储到哈希表中的元素，都配有一个唯一的标识（又称“索引”或者“键”），用户想查找哪个元素，凭借该元素对应的标识就可以直接找到它，无需遍历整个哈希表。

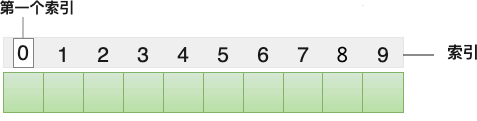
多数场景中，哈希表是在数组的基础上构建的，下图给大家展示了一个普通的数组：

使用数组构建哈希表，最大的好处在于：

可以直接将数组下标当作已存储元素的索引，不再需要为每个元素手动配置索引，极大得简化了构建哈希表的难度。

我们知道，在数组中查找一个元素，除非提前知晓它存储位置处的下标，否则只能遍历整个数组。

哈希表的解决方案是：各个元素并不从数组的起始位置依次存储，它们的存储位置由专门设计的函数计算得出，我们通常将这样的函数称为哈希函数。

哈希函数类似于数学中的一次函数，我们给它传递一个元素，它反馈给我们一个结果值，这个值就是该元素对应的索引，也就是存储到哈希表中的位置。

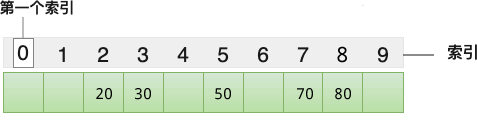
举个例子，将 {20, 30, 50, 70, 80} 存储到哈希表中，我们设计的哈希函数为 y=x/10，最终各个元素的存储位置如下图所示：

在图 2 的基础上，假设我们想查找元素 50，只需将它带入 y=x/10 这个哈希函数中，计算出它对应的索引值为 5，直接可以在数组中找到它。

借助哈希函数，我们提高了数组中数据的查找效率，这就是哈希表存储结构。

构建哈希表时，哈希函数的设计至关重要。假设将 {5, 20, 30, 50, 55} 存储到哈希表中，哈希函数是 y=x%10，各个元素在数组中的存储位置如下图所示：

可以看到，5 和 55 以及 20、30 和 50 对应的索引值是相同的，它们的存储位置发生了冲突，我们习惯称为哈希冲突或者哈希碰撞。

设计一个好的哈希函数，可以降低哈希冲突的出现次数。哈希表提供了很多解决哈希冲突的方案，比如线性探测法、再哈希法、链地址法等。

本节我们使用线性探测法解决哈希冲突，解决方法是：当元素的索引值（存储位置）发生冲突时，从当前位置向后查找，直至找到一个空闲位置，作为冲突元素的存储位置。仍以图 3 中的哈希表为例，使用线性探测法解决哈希冲突的过程是：

• 元素 5 最先存储到数组中下标为 5 的位置；
• 元素 20 最先存储到数组中下标为 0 的位置；
• 元素 30 的存储位置为 0，和 20 冲突，根据线性探测法，从下标为 0 的位置向后查找，下标为 1 的存储位置空闲，用来存储 30；
• 元素 50 的存储位置为 0，和 20 冲突，根据线性探测法，从下标为 0 的位置向后查找，下标为 2 的存储位置空闲，用来存储 50；
• 元素 55 的存储位置为 5，和 5 冲突，根据线性探测法，从下标为 5 的位置向后查找，下标为 6 的存储位置空闲，用来存储 55。

借助线性探测法，最终 {5, 20, 30, 50, 55} 存储到哈希表中的状态为：

假设我们从图 4 所示的哈希表中查找元素 50，查找过程需要经过以下几步：

• 根据哈希函数 y=x%10，目标元素的存储位置为 0，但经过和下标为 0 处的元素 20 比较，该位置存储的并非目标元素；
• 根据线性探测法，比较下标位置为 1 处的元素 30，也不是目标元素；
• 继续比较下标位置为 2 的元素 50，成功找到目标元素。

对于发生哈希冲突的哈希表，尽管查找效率会下降，但仍比一些普通存储结构（比如数组）的查找效率高。

2.算法步骤

哈希查找算法就是利用哈希表查找目标元素的算法。对于给定的序列，该算法会先将整个序列存储到哈希表中，然后再查找目标元素。

待查找的数据 ----> 数组的索引（键值）

3.代码实现

3.1.算法实现

//自定义哈希函数
int hash(int value) {
    return value / 10;
}
//创建哈希表
void creatHash(int arr[5], int hashArr[N]) {
    int i,index;
    //将序列中每个元素存储到哈希表
    for (i = 0; i < 5; i++) {
        index = hash(arr[i]);
        while(hashArr[index % N] != 0) {
            index++;
        }
        hashArr[index] = arr[i];
    }
}

//实现哈希查找算法，hashArr 表示哈希表，value 为要查找的目标元素
int hash_search(int* hashArr, int value) {
    int hashAdd = hash(value);             //查找目标元素所在的索引
    while (hashArr[hashAdd] != value) {    // 如果索引位置不是目标元素，则发生了碰撞
        hashAdd = (hashAdd + 1) % N;       // 根据线性探测法，从索引位置依次向后探测
        //如果探测位置为空，或者重新回到了探测开始的位置（即探测了一圈），则查找失败
        if (hashArr[hashAdd] == 0 || hashAdd == hash(value)) {
            return -1;
        }
    }
    //返回目标元素所在的数组下标
    return  hashAdd;
}

3.2.测试程序

#include 
#define N 10   //指定哈希表的长度
int main()
{
    int hashAdd;
    int hashArr[N] = { 0 };//hash表
    int arr[5] = {10,20,30,40,50};
    creatHash(arr, hashArr);//hashArr索引1~5中保存着数据
    hashAdd = hash_search(hashArr, 50);
    //如果返回值为 -1，表明查找失败，反之则返回目标元素所在的位置
    if (hashAdd == -1) {
        printf("查找失败\n");
    }
    else {
        printf("查找成功，目标元素所在哈希表中的下标为：%d", hashAdd);
    }
    return 0;
}

4.程序结果