2018 ICML | Junction Tree Variational Autoencoder for Molecular Graph Generation

2018 ICML | Junction Tree Variational Autoencoder for Molecular Graph Generation

Paper: https://arxiv.org/pdf/1802.04364
Code: https://github.com/wengong-jin/icml18-jtnn

2018 ICML | 用于分子图生成的连接树变分自动编码器

本文是Wengong Jin团队2018年发表于ICML的文章，其主要工作是直接实现分子图，通过连接树变分自编码器通过两个阶段生成分子图，首先在化学子结构上生成一个树形结构支架，然后通过图形信息传递网络将它们组合成一个分子。这种方法允许逐步扩大分子，同时保持每一步的化学有效性。该方法在多个任务上评估比之前的最先进的基线性能要好得多。

药物发现任务由两个互补的子任务:

1. 学习以一种连续的方式表示分子，以促进预测和优化其属性(编码);
2. 学习将优化的连续表示映射回具有改进性质的分子图(解码)

以前生成方式：逐节点生成图形来解决这个问题，但这种方法对于分子来说并不理想。

作者使用两个阶段的分子图，利用有效的子图作为组件。整体生成方法，作为一个连接树变分自编码器，

1. 首先生成一个树结构的对象(连接树)，它的作用是表示子图组件的脚手架和它们的相对排序。这些组件是使用树分解从训练集自动提取的有效化学子结构，并用作构建块。
2. 在第二阶段，子图(树中的节点)被组装成一个分子图。

Junction Tree Variational Autoencoder

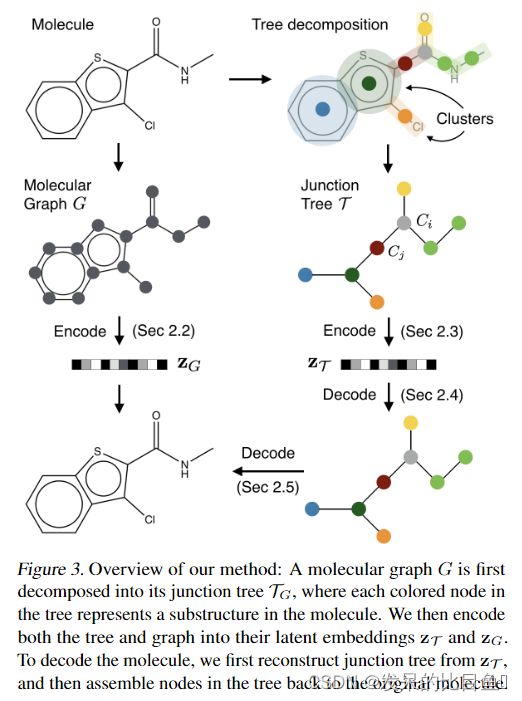
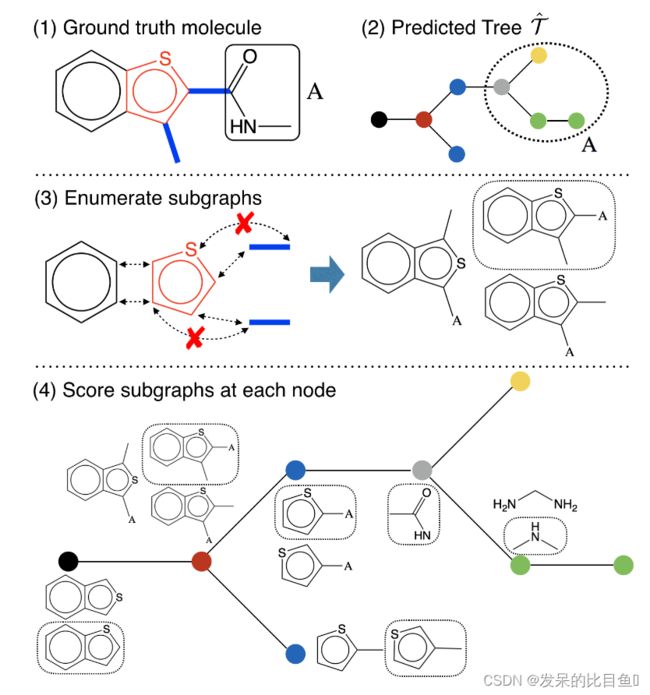
作者将每个分子解释为从有效成分词汇表中选择的子图构建。当将分子编码为矢量表示，以及将潜在矢量解码回有效的分子图时，这些组件都被用作构建模块。这种观点的关键优势在于，解码器可以通过利用有效组件的集合以及它们如何相互作用来实现一个有效分子，而不是试图通过化学无效的中间体一个原子一个原子地构建分子原子(图2)。

作者将分子编码为两部分的潜在表示$z=[z_T,z_G]$，其中$z_T$编码树结构和树中的簇而没有完全捕获簇是如何确切地相互连接的。$z_G$对图进行编码，以捕获细粒度的连接性。这两个部分都是由树和图编码器$q(z_T|T)$和$q(z_G|G)$创建。然后，潜伏表示被解码回一个分子图。如图3所示，使用基于$z_T$中的信息的树解码器$p(T|z_T)$来再现连接树。其次，利用图译码器$p(G|t,z_G)$预测连接树中簇之间的细粒度连通性，从而实现全分子图。连接树方法允许在生成过程中保持化学可行性。

符号:
分子图定义为$G=(V,E)$，其中$V$是原子的集合(顶点)，$E$是键的集合(边)。设$N(x)$是$x$的邻居。将sigmoid函数表示为$\sigma (\cdot )$，将ReLU函数表示为$\tau (\cdot )$。用$i,j,k$表示树中的节点用$u,v,w$表示图中的节点。

Junction Tree

树分解将图$G$映射为连接树，通过将某些顶点收缩为单个节点，使$G$变得无循环。形式上，给定图$G$，连接树$T_G=(V,E,\chi )$是一棵连通标记树，节点集$V=C_1,\cdot \cdot \cdot ,C_n$，边集设置为$E$。

1. 每个节点或簇$C_i=(V_i,E_i)$是$G$的诱导子图，满足以下约束条件。所有簇的并集等于$G$，即${\cup }_i$ $V_i=V,{\cup }_i{E}_i=E$。
2. 运行交叉口:对于所有集群$C_i,C_j$和$C_k$, $V_i{V}_j{V}_k$，如果$C_k$在从$C_i$到$C_j$的路径上。

Tree Decomposition of Molecules 在这里，分子树分解算法，它的根源在于化学。给定一个图$G$，首先找出它所有的简单环，它的边不属于任何环。如果两个简单的环有两个以上重叠的原子，它们就会合并在一起，因为它们构成了一种特定的结构，称为桥接化合物。这些圈或边中的每一条都被认为是一个簇。接下来，通过在所有相交的簇之间添加边来构造一个簇图。最后，选择其中一棵生成树作为G的连接树(图3)。

Graph Encoder

每条边$(u,v)\in E$都有一个特征向量$x_{uv}$，表示其键类型，两个隐藏向量${\nu }_{uv}$和${\nu }_{vu}$表示从$u$到$v$的信息，反之亦然。由于图的环状结构，消息以环状的信息传播方式交换:

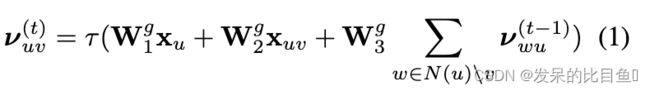
其中${\nu }_{uv}^{(t)}$是在第$t$次迭代中计算的消息，用${\nu }_{uv}^{(0)}=0$初始化。经过$T$步迭代后，这些信息聚合为每个顶点的潜在向量，从而捕获其局部图形结构

最终图表为$h_G={\Sigma }_i{h}_i/|V|$。从$h_G$计算两个独立仿射层，分别近似值的平均${\mu }_g$和对数方差量${\sigma }_g$是计算出来的。从高斯$N({\mu }_g，{\sigma }_g)$中采样$Z_g$。

Tree Encoder

每个簇$C_i$由一个表示其标签类型的一热编码$x_i$表示。每条边$(C_i,C_j)$与两个消息向量$m_{ij}$和$m_{ji}$相关联。任意的叶节点作为根节点，并分两个阶段传播消息。在第一个自底向上阶段，消息从叶子节点初始化，然后迭代地向根传播。在自顶向下阶段，消息从根节点传播到所有叶节点。消息$m_{ij}$更新为

其中GRU为门控循环单元用于树消息传递

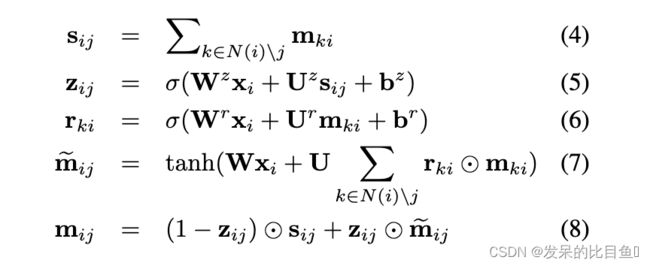
传递的消息遵循调度，其中mij仅在其所有前体{mki |k N(i)\j}都已计算时才计算。这种架构设计的动机是基于树的信念传播算法，因此与图形编码器不同。

在消息传递后，我们通过聚合每个节点的内部消息来得到每个节点$h_i$的潜在表示:

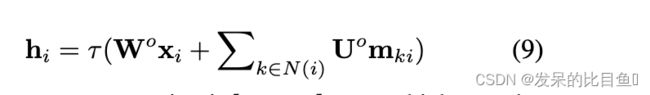
最终的树表示是KaTeX parse error: Double subscript at position 4: h_T_̲G = h_{root}，它编码了一个有根树$(T,root)$。与图编码器不同，作者不应用节点平均池化，因为它混淆了树解码器首先生成哪个节点。KaTeX parse error: Double subscript at position 4: z_T_̲G的采样方式与图形编码器类似。为简便起见，从现在起，将KaTeX parse error: Double subscript at position 4: z_T_̲G缩写为$z_T$。首先，它用于计算$z_T$，只需要网络的自底向上阶段。其次，在从$z_T$解码出树$T$后，它用于计算整个$T$上的消息$m_{ij}$，在图解码期间提供每个节点的基本上下文。需要自上而下和自下而上两个阶段。

Tree Decoder

在每个时间步骤中，一个节点从当前树中的其他节点接收信息，以便进行这些预测。增量构造树时，信息通过消息向量hij传播。形式上，设$\tilde{E}=\{(i_1,j_1)，\cdot \cdot \cdot ，(i_m,j_m)\}$是深度第一次遍历$T=(V,E)$时遍历的边，其中$m=2|E|$，每条边都在两个方向遍历。模型在时刻$t$访问它。设${\tilde{E}}_t$为$\tilde{E}$中的第一个$t$条边。消息命中，$h_{i_t,j_t}$通过之前的消息更新

其中GRU是与树编码器相同的循环单位。

Topological Prediction 通过结合$z_T$、节点特征$x_{i_t}$和消息$h_k$，通过一个隐层网络和一个sigmoid函数来计算概率

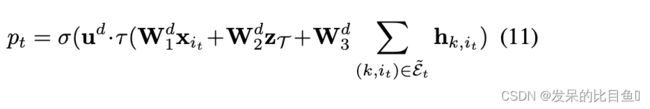
Label Prediction 当从父节点$i$生成一个子节点$j$时，预测它的节点标签为

其中$q_j$是词汇表$x$上的分布。当$j$是根节点时，它的父节点$i$是虚拟节点，并且$h_{ij}=0$。

learning 树解码器的目标是最大化似然概率$p(T|z_T)$。设${\hat{p}}_t\{0,1\}$和$q_j$为大地真值拓扑和标签值，解码器使接下来的交叉熵损失最小化

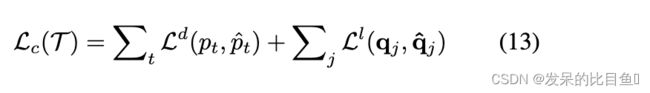
Decoding & Feasibility Check
为了确保可以将采样的树实现为有效的分子，我们将集合$x_i$定义为与节点$i$及其当前邻居化学兼容的群集标签。当从节点$i$产生子节点$j$时，通过掩盖无效标签，从$x_i$中用$x_i$进行了重新归一化的分布$q_j$的标签。

Graph Decoder

我们模型的最后一步是复制一个分子图$G$，它是预测连接树$T=(V,E)$的基础。注意，这一步不是确定性的，因为可能有很多分子对应于同一连接树。潜在的自由度与相邻集群$C_i$和$C_j$如何作为子图相互连接有关。目标是将子图(树中的节点)组装成正确的分子图。设$G(T)$是连接树为$T$的图的集合，由$T=(V,E)$编码的图$G$是一个结构化预测:

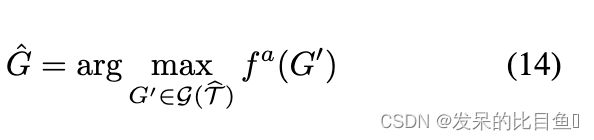
利用索引${\alpha }_v$标记原子在连接树中的位置，并沿着树编码算法得到的边$(i,j)$检索信息$m_{i,j}$，总结$i$下的子树。与子图$G_i$中的原子和键相关的神经信息被获得并聚合到KaTeX parse error: Double subscript at position 4: h_G_̲i中，这与编码步骤类似，但具有不同的参数:

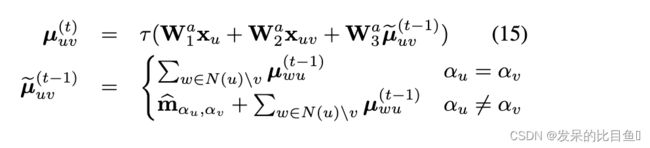
Learning. 学习图解码器参数，以最大程度地在每个树节点上预测地面真图$G$的正确子图$G_i$的对数似然

Complexity 根据我们的树状分解，任何两个簇最多共享两个原子，只需要合并最多两个原子或一个键。通过修剪化学无效的子图和合并同构图，在标准ZINC药物数据集上测试时，平均$|G_i|$=4。因此，在集群数量上，JT-VAE的计算复杂度是线性的，可以很好地缩放到大型图。