数值分析A-实验作业1 - 3.3

数值分析A-实验作业1 - 3.3

说明

注：为了便于校验结果，本文为实验报告的补充

程序结构

• myGauss.m：完全主元Gauss消去法求解
• myJacobi.m：J法求解
• myGS.m：GS法求解
• mySOR.m：SOR法加速迭代求解
• myGauss2.m：维数$n$增大_完全主元Gauss消去法求解
• myJacobi2.m：维数$n$增大_J法求解
• myGS2.m：维数$n$增大_GS法求解
• mySOR2.m：维数$n$增大_SOR法加速迭代求解

实验3.3（病态的线性方程组的求解）

问题提出：

理论的分析表明，求解病态的线性方程组是困难的.实际情况是否如此，会出现怎样的现象呢？

实验内容：

考虑方程组$Hx=b$的求解，其中系数矩阵$H$出为Hilbert 矩阵，
$$H=(h_{i,j}{)}_{n\times n}，h_{i,j}=\frac{1}{i+j-1}，i,j=1,2,\cdots ,n$$
这是一个著名的病态问题．通过首先给定解(例如取为各个分量均为1）再计算出右端的办法给出确定的问题。

实验要求

1. 选择问题的维数为6，分别用 Gauss 消去法（即LU 分解）、J迭代方法、GS 迭代法和 SOR 迭代求解方程组，其各自的结果如何？將计算结果与问题的解比较,结论如何.
2. 逐步增大问题的维数，仍然用上述的方法来解它们，计算的结果如何？计算的结果说明了什么？
3. 讨论病态问题求解的算法.

实验参数：

• 由题可知：精确解为$x^{\ast }=[1,1,1,1,1,1]$
• 选取初值$x=[0,0,0,0,0,0]$，维数$n=6$，
• 设置迭代终止条件： ∥ x ( k + 1 ) − x ( k ) ∥ ∞ < 1 × 1 0 − 6 \left \| x_{(k+1)} -x_{(k)} \right \|_{\infty}<1\times 10^{-6} ​x(k+1)​−x(k)​ ​∞​<1×10−6

解：

实验要求1.

选择问题的维数为6，分别用 Gauss 消去法（即LU 分解）、J迭代方法、GS 迭代法和 SOR 迭代求解方程组，其各自的结果如何？將计算结果与问题的解比较,结论如何.

（1）Gauss消去法

Gauss法求解方程组，程序myGauss.m

%-----  code 完全选主元Gauss消去 -----
%-----  code 完全选主元Gauss消去 -----
%-----  code 完全选主元Gauss消去 -----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求1. -------------------------


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---

n = input('Input n = ');
tol = 1e-6;%迭代终止条件
H = zeros(n,n);
x = ones(n,1);
x0 = zeros(n,1);

H=hilb(n); %生成n阶Hilbert矩阵
b = H*x;%取各个分量均为1 求解b

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
disp('------- 精确解为x ------- ');
x = ones(n,1)

disp('------- 完全选主元Gauss消元法解为x1 -------');
x1 = Gauss2(H,b)

disp('------- 误差为 \left\| x-x^* \right\| _{\infty} -------');
norm(x-x1,inf)
% --- --- --- --- --- ---定义判断函数 --- --- --- --- --- ---
function r= iszero(a)
    if(abs(a-0)<1e-10)
        r=1;
        disp('被除数为0，方程组无解 或有无穷解')
    else
        r=0;
    end
end
% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义完全选主元Gauss消去函数 --- --- --- --- --- 
function x = Gauss2(A,b) %Gauss2为完全主元高斯消去法
    
    n = size(A,1);
    x = zeros(n,1);
    %l为乘数
    l = zeros(n,1);
    %e为初等变换矩阵，用于列交换之后将最后的解x的位置更正
    e = eye(n);
    %迭代n-1次
    for k = 1:n-1
        %寻找最大主元
        MAX1 = max(abs(A(k:n,k:n)));
        MAX = max(MAX1);
        [index1,index2] = find(abs(A(k:n,k:n))==MAX,1);
        index1 = index1+k-1;
        index2 = index2+k-1;
        %交换行、列
        if k ~= index1
            A([k,index1],:) = A([index1,k],:);
            b([k,index1],:) = b([index1,k],:);
        end
        if k ~= index2
            A(:,[k,index2]) = A(:,[index2,k]);
            e(:,[k,index2]) = e(:,[index2,k]);
        end
        for i=k+1:n
            l(i) = A(i,k)/A(k,k);
            b(i) = b(i) - l(i)*b(k);
            for j =k:n
                A(i,j) = A(i,j) - l(i)*A(k,j); 
            end
        end
    end

    x(n) = b(n)/A(n,n);
    for k=n-1:-1:1
        w=0;
        for j = k+1:n
            w = w + A(k,j)*x(j);
        end
        x(k) = (b(k)-w)/A(k,k);
    end
    x=e*x;

end

（2）J迭代法

J法求解方程组，程序myJacobi.m

%-----  code Jacobi迭代法 -----
%-----  code Jacobi迭代法 -----
%-----  code Jacobi迭代法 -----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求1. -------------------------


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---

n = input('Input n = ');
tol = 1e-6;%迭代终止条件
H = zeros(n,n);
x = ones(n,1);
x0 = zeros(n,1);%初值

H=hilb(n); %生成n阶Hilbert矩阵
b = H*x;%取各个分量均为1 求解b

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
disp('------- 精确解为x ------- ');
x = ones(n,1)

disp('------- J法_output -------');

[x_J, times_J] = myJacobi_f(H,b,x0,tol); %J法求解

disp('J法求得的解：')
disp(x_J);
fprintf('J法迭代次数：%d\n',times_J);
disp('------- J法误差为 \left\| x-x^* \right\| _{\infty} -------');
norm(x-x_J,inf)
% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义J法迭代函数 --- --- --- --- ---

function [x,times] = myJacobi_f( A,b,x0,tol )
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);
    times = 0;
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    B = D\(L+U);
    fprintf('J法矩阵范数：%16.15f\n',norm(B,1));
    fprintf('J法谱半径：%16.15f\n',max(abs(eig(B))));
    fprintf('J法收敛速度：%16.15f\n',-log(max(abs(eig(B)))));
    f = D\b;
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = B*x_last + f;
        times = times+1;
        delta_x = x - x_last;
    end
end

（3）GS迭代法

GS法求解方程，程序myGS.m

%-----  code GS迭代法 -----
%-----  code GS迭代法 -----
%-----  code GS迭代法 -----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求1. -------------------------


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---

n = input('Input n = ');
tol = 1e-6;%迭代终止条件
H = zeros(n,n);
x = ones(n,1);
x0 = zeros(n,1);%初值

H=hilb(n); %生成n阶Hilbert矩阵
b = H*x;%取各个分量均为1 求解b

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
disp('------- 精确解为x ------- ');
x = ones(n,1)

disp('------- GS迭代法_output -------');

[x_GS, times_GS,final_delta_x] = myGS_f(H,b,x0,tol); %GS求解

disp('GS法求得的解：')
disp(x_GS);
fprintf('GS法迭代次数：%d\n',times_GS);
fprintf('最后两次迭代结果差值：%16.15e\n',final_delta_x);

disp('------- GS法误差为 \left\| x-x^* \right\| _{\infty} -------');
fprintf('GS法误差：%16.15e\n',norm(x-x_GS,inf));
fprintf('GS法误差：%16.15f\n',norm(x-x_GS,inf));

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义GS迭代函数 --- --- --- --- --- 

function [x,times,final_delta_x] = myGS_f( A,b,x0,tol )
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);
    times = 0;
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    G = (D-L)\U;
    fprintf('GS法矩阵范数：%16.15f\n',norm(G,1));
    fprintf('GS法收敛速度：%16.15e\n',-log(max(abs(eig(G)))));
    fg = (D-L)\b;
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = G*x_last + fg;
        times = times+1;
        delta_x = x - x_last;
    end
    final_delta_x = norm(delta_x,inf);
    
    
end

（4）SOR迭代法

SOR法求解方程，通过在区间$[0.01,1.99]$，步长0.001，循环寻找使得迭代次数最少的松弛因子，得到结果$\omega =0.2042$，迭代次数为552次，程序mySOR.m

%-----  code SOR迭代法 -----
%-----  code SOR迭代法 -----
%-----  code SOR迭代法 -----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求1. -------------------------


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---

n = input('Input n = ');
tol = 1e-6;%迭代终止条件
H = zeros(n,n);
x = ones(n,1);
x0 = zeros(n,1);%初值

H=hilb(n); %生成n阶Hilbert矩阵
b = H*x;%取各个分量均为1 求解b

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
disp('------- 精确解为x ------- ');
x = ones(n,1)

disp('------- SOR法_output -------');

times_SOR = Inf;

for w=0.01:0.0001:1.99 %遍历寻找迭代次数最少的松弛因子
    [x_SOR_temp, times_SOR_temp,norm_Lw_temp,vrho_Lw_temp,w_temp,delta_x_temp] = mySOR_f(H,b,x0,tol,w);%SOR法求解
    if times_SOR_temp < times_SOR
        times_SOR = times_SOR_temp;
        x_SOR = x_SOR_temp;
        norm_Lw = norm_Lw_temp;
        vrho_Lw = vrho_Lw_temp;
        delta_x = delta_x_temp;
        w0 = w;

    end
end


fprintf('SOR法矩阵范数：%16.15f\n',norm_Lw);
fprintf('SOR法谱半径：%16.15f\n',vrho_Lw);
fprintf('SOR法收敛速度：%16.15e\n',-log(max(abs(eig(vrho_Lw)))));
fprintf('SOR法迭代次数最少的松弛因子：%16.15f\n',w0);
fprintf('SOR法最后两次迭代结果差值：%16.15e\n',delta_x);



disp('SOR法求得的解：')
x_SOR
fprintf('SOR法迭代次数：%d\n',times_SOR);



disp('------- SOR法误差为 \left\| x-x^* \right\| _{\infty} -------');
norm(x-x_SOR,inf)
% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义SOR法迭代函数 --- --- --- --- ---

function [x,times,norm_Lw,vrho_Lw,w,final_delta_x] = mySOR_f(A,b,x0,tol,w)
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);

    times = 0; %迭代次数
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    Lw = (D-w*L)\((1-w)*D + w*U);

    norm_Lw = norm(Lw,1);%SOR法矩阵范数
    vrho_Lw = max(abs(eig(Lw)));%SOR法谱半径


%     fprintf('SOR法矩阵范数：%16.15f\n',norm(Lw,1));
%     fprintf('SOR法谱半径：%16.15f\n',max(abs(eig(Lw))));
%     fprintf('SOR法松弛因子：%16.15f\n',w);

    fw = w*((D-w*L)\b);
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = Lw*x_last + fw;
        times = times+1;
        delta_x = x - x_last;
    end
    final_delta_x = norm(delta_x,inf);
end

实验结果1.

		实验要求1.结果
算法	Gauss消去法	J法	GS法	SOR法(松弛因子为0.2042)
计算结果	[ 0.999999999999081 1.000000000026098 0.999999999823895 1.000000000457345 0.999999999495697 1.000000000198576 ] \begin{bmatrix} 0.999999999999081\\ 1.000000000026098\\ 0.999999999823895\\ 1.000000000457345\\ 0.999999999495697\\ 1.000000000198576\\\end{bmatrix} ​0.9999999999990811.0000000000260980.9999999998238951.0000000004573450.9999999994956971.000000000198576​ ​	[ I n f I n f N a N N a N N a N N a N ] \begin{bmatrix} Inf\\ Inf\\ NaN\\ NaN\\ NaN\\ NaN\\\end{bmatrix} ​InfInfNaNNaNNaNNaN​ ​	[ 0.999886162982190 1.001612735704288 0.995761538789744 0.999352008537048 1.009993347163575 0.993301594085438 ] \begin{bmatrix} 0.999886162982190\\ 1.001612735704288\\ 0.995761538789744\\ 0.999352008537048\\ 1.009993347163575\\ 0.993301594085438\end{bmatrix} ​0.9998861629821901.0016127357042880.9957615387897440.9993520085370481.0099933471635750.993301594085438​ ​	[ 0.999738428346001 1.003504458042611 0.989448933062251 1.005906760245761 1.010291044305880 0.990936872483232 ] \begin{bmatrix} 0.999738428346001\\ 1.003504458042611\\ 0.989448933062251\\ 1.005906760245761\\ 1.010291044305880\\ 0.990936872483232\end{bmatrix} ​0.9997384283460011.0035044580426110.9894489330622511.0059067602457611.0102910443058800.990936872483232​ ​
谱半径		4.308531034793304	0.999998299252624	0.999999806885223
收敛速度		-1.460597018826739	1.700748822315769e-06	1.931147952609835e-07
迭代次数			14522	552
最后两次差值			9.999918834102672e-07	9.916767973461305e-07
误差	5.043034878582375e-10	NaN	9.993347163575361e-03	1.0551066937749e02

总结分析1.

在所设实验参数下，

• 完全选主元Gauss消去法计算误差最小；
• J法谱半径大于1，迭代不收敛，GS法和SOR法谱半径均小于1，迭代收敛；
• 相比于GS法收敛需要14522步，松弛因子选取0.2042时，SOR法仅需迭代522就收敛，但精度有所下降，渐进收敛速率为GS法的0.11，并不是最优松弛因子；
• 实验中还发现所设置的松弛因子循环步长，会显著影响找到使得迭代次数最少的松弛因子，例如设置寻找步长为0.01，找到的松弛因子为1.85，且所得误差较小，只不过不满足程序设计的迭代次数最少条件，没有输出。

实验要求2.

逐步增大问题的维数，仍然用上述的方法来解它们，计算的结果如何？计算的结果说明了什么？

实验结果2.

分别使用Gauss消去法、J法、GS法、SOR法进行计算；阶数选择6、8、10、15、20、25；其中，SOR法的松弛因子是自动选取的，为了减小计算量，步长调整为0.01，其余与实验要求1.一致，带入计算，可得：

（1）Gauss消去法——程序文件 myGauss2.m

%-----  code 完全选主元Gauss消去 for 实验3.3 (2)-----
%-----  code 完全选主元Gauss消去 for 实验3.3 (2)-----
%-----  code 完全选主元Gauss消去 for 实验3.3 (2)-----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求2. -------------------------
disp("---------  Gauss法_output  -------");


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---
for n = 1:1:20

%     n = input('Input n = ');
    tol = 1e-6;%迭代终止条件

    x = ones(n,1);
    x0 = zeros(n,1);
    
    H=hilb(n); %生成n阶Hilbert矩阵
    b = H*x;%取各个分量均为1 求解b
    
    % --- --- --- --- --- --- --- --- --- ------ --- --- --- ---
    
    
    % --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 

    x1 = Gauss2(H,b);
    fprintf('n=：%2d,  误差为: %18.14f \n',n,norm(x-x1,inf));

end



% --- --- --- --- --- ---定义判断函数 --- --- --- --- --- ---
function r= iszero(a)
    if(abs(a-0)<1e-10)
        r=1;
        disp('被除数为0，方程组无解 或有无穷解')
    else
        r=0;
    end
end
% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义完全选主元Gauss消去函数 --- --- --- --- --- 
function x = Gauss2(A,b) %Gauss2为完全主元高斯消去法
    
    n = size(A,1);
    x = zeros(n,1);
    %l为乘数
    l = zeros(n,1);
    %e为初等变换矩阵，用于列交换之后将最后的解x的位置更正
    e = eye(n);
    %迭代n-1次
    for k = 1:n-1
        %寻找最大主元
        MAX1 = max(abs(A(k:n,k:n)));
        MAX = max(MAX1);
        [index1,index2] = find(abs(A(k:n,k:n))==MAX,1);
        index1 = index1+k-1;
        index2 = index2+k-1;
        %交换行、列
        if k ~= index1
            A([k,index1],:) = A([index1,k],:);
            b([k,index1],:) = b([index1,k],:);
        end
        if k ~= index2
            A(:,[k,index2]) = A(:,[index2,k]);
            e(:,[k,index2]) = e(:,[index2,k]);
        end
        for i=k+1:n
            l(i) = A(i,k)/A(k,k);
            b(i) = b(i) - l(i)*b(k);
            for j =k:n
                A(i,j) = A(i,j) - l(i)*A(k,j); 
            end
        end
    end

    x(n) = b(n)/A(n,n);
    for k=n-1:-1:1
        w=0;
        for j = k+1:n
            w = w + A(k,j)*x(j);
        end
        x(k) = (b(k)-w)/A(k,k);
    end
    x=e*x;

end

可以发现：Gauss消去法在维数$n<11$时，误差还可以接受，随着维数$n$增大，误差不断放大。说明对于病态方程，Gauss消去法不稳定。

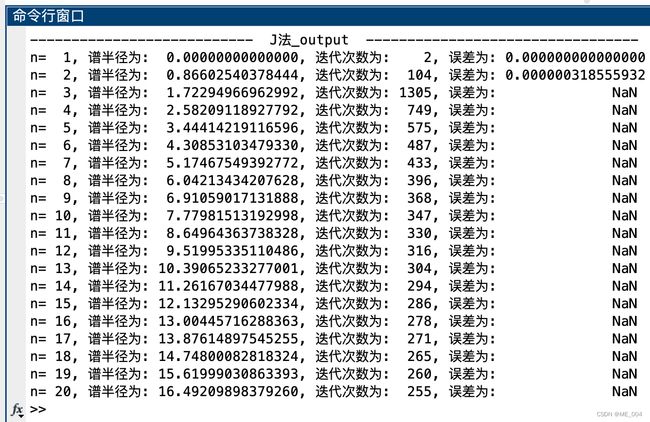
（2）J法——程序文件 myJacobi2.m

%-----  code Jacobi迭代法 for 实验3.3 (2)-----
%-----  code Jacobi迭代法 for 实验3.3 (2)-----
%-----  code Jacobi迭代法 for 实验3.3 (2)-----




clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求2. -------------------------


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---

disp("---------------------------  J法_output  ---------------------------------");

for n = 1:1:20
%     n = input('Input n = ');
    tol = 1e-6;%迭代终止条件
    x = ones(n,1);
    x0 = zeros(n,1);%初值
    
    H=hilb(n); %生成n阶Hilbert矩阵
    b = H*x;%取各个分量均为1 求解b
    
    % --- --- --- --- --- --- --- --- --- ------ --- --- --- ---
    
    
    % --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
    
    [x_J, times_J,rhoB] = myJacobi_f(H,b,x0,tol); %J法求解
    fprintf('n= %2d, 谱半径为: %17.14f, 迭代次数为: %4d, 误差为: %16.15f \n',n,rhoB,times_J,norm(x-x_J,inf));

end

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义J法迭代函数 --- --- --- --- ---

function [x,times,rhoB] = myJacobi_f( A,b,x0,tol )
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);
    times = 0;
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    B = D\(L+U);
%     fprintf('J法矩阵范数：%16.15f\n',norm(B,1));
%     fprintf('J法谱半径：%16.15f\n',max(abs(eig(B))));
%     fprintf('J法收敛速度：%16.15f\n',-log(max(abs(eig(B)))));
    rhoB = max(abs(eig(B)));
    f = D\b;
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = B*x_last + f;
        times = times+1;
        delta_x = x - x_last;
    end
end

可以发现：J法在维数$n<3$时，谱半径小于1，J法迭代收敛，误差还可以接受，随着维数$n$增大，谱半径大于1，J法不收敛。说明对于病态方程，J法并不适用。

（3）GS法——程序文件 myGS2.m

%-----  code GS迭代法 for 实验3.3 (2)-----
%-----  code GS迭代法 for 实验3.3 (2)-----
%-----  code GS迭代法 for 实验3.3 (2)-----





clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求2. -------------------------

disp("-----------------------------------------------  GS法_output  -----------------------------------------------");

% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---
for n = 1:1:30
%     n = input('Input n = ');
    tol = 1e-6;%迭代终止条件
    x = ones(n,1);
    x0 = zeros(n,1);%初值
    
    H=hilb(n); %生成n阶Hilbert矩阵
    b = H*x;%取各个分量均为1 求解b
    
    % --- --- --- --- --- --- --- --- --- ------ --- --- --- ---
    
    
    % --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
    
    [x_GS, times_J,rhoG,final_delta_x] = myGS_f(H,b,x0,tol); %J法求解
    fprintf('n= %2d, 谱半径为: %17.14f, 迭代次数为: %5d, 最后两次迭代差值为: %17.14f, 误差为: %16.15f \n',n,rhoG,times_J,final_delta_x,norm(x-x_GS,inf));

end

% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义GS法迭代函数 --- --- --- --- ---


function [x,times,rhoG,final_delta_x] = myGS_f( A,b,x0,tol )
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);
    times = 0;
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    G = (D-L)\U;
%     fprintf('GS法矩阵范数：%16.15f\n',norm(G,1));
%     fprintf('GS法收敛速度：%16.15e\n',-log(max(abs(eig(G)))));
    rhoG = max(abs(eig(G)));
    fg = (D-L)\b;
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = G*x_last + fg;
        times = times+1;
        delta_x = x - x_last;
    end
    final_delta_x = norm(delta_x,inf);
    
    
end

可以发现：GS法在维数$n<12$时，谱半径小于1，GS法迭代收敛，误差较小；随着维数$n$增大，谱半径显示为1，可能是MATLAB已经出现舍入误差，计算结果的误差虽然不断增大但仍可接受，最大缺点在于迭代次数较多。

说明对于Hilbert矩阵为系数矩阵的病态方程，GS法可以收敛，但需要迭代多次，且随着维数的增加达到收敛的次数会不断增加，计算效率低。

（4）SOR法——程序文件 mySOR2.m

%-----  code SOR迭代法 for 实验3.3 (2)-----
%-----  code SOR迭代法 for 实验3.3 (2)-----
%-----  code SOR迭代法 for 实验3.3 (2)-----





clc %清除命令窗口的内容
clear all; %清除工作空间的所有变量，函数，和MEX文件
format long ; %设置输出显示格式为16位有效数字

%---------------------  数值分析 实验3.3 病态的线性方程组的求解 ---------------------
    %H  系数矩阵
    %b  右端项
    %n  阶数
%------------------------  实验要求2. -------------------------
disp("-----------------------------------------------  SOR法_output  -----------------------------------------------");


% --- --- --- --- --- ---输入矩阵H和b --- --- --- --- --- ---
for n = 1:1:30

    tol = 1e-6;%迭代终止条件
    x = ones(n,1);
    x0 = zeros(n,1);%初值
    
    H=hilb(n); %生成n阶Hilbert矩阵
    b = H*x;%取各个分量均为1 求解b
    
    % --- --- --- --- --- --- --- --- --- ------ --- --- --- ---
    
    
    % --- --- --- --- --- --- 求解 --- --- --- --- --- --- --- 
    
    times_SOR = Inf;
    
    for w=0.01:0.01:1.99 %遍历寻找迭代次数最少的松弛因子
        [x_SOR_temp, times_SOR_temp,norm_Lw_temp,vrho_Lw_temp,w_temp,delta_x_temp] = mySOR_f(H,b,x0,tol,w);%SOR法求解
        if times_SOR_temp < times_SOR
            times_SOR = times_SOR_temp;
            x_SOR = x_SOR_temp;
            norm_Lw = norm_Lw_temp;
            vrho_Lw = vrho_Lw_temp;
            delta_x = delta_x_temp;
            w0 = w;
        end
    end
    
    fprintf('n= %2d, w= %6f, 谱半径为: %17.14f, 迭代次数为: %5d, 最后两次迭代差值为: %17.14e, 误差为: %16.15e \n',n,w0,vrho_Lw,times_SOR,delta_x,norm(x-x_SOR,inf));


end    



% --- --- --- --- --- --- --- --- --- ------ --- --- --- ---


% --- --- --- --- --- ---定义SOR法迭代函数 --- --- --- --- ---

function [x,times,norm_Lw,vrho_Lw,w,final_delta_x] = mySOR_f(A,b,x0,tol,w)
    %UNTITLED8 此处显示有关此函数的摘要
    %   此处显示详细说明
    n = size(A,1);
    L = zeros(n,n);
    D = zeros(n,n);
    delta_x = ones(n,1);

    times = 0; %迭代次数
    for i=1:n
        D(i,i) = A(i,i);
    end
    for i=2:n
        for j=1:i-1
            L(i,j) = -A(i,j);
        end
    end

    U = D-L-A;
    Lw = (D-w*L)\((1-w)*D + w*U);

    norm_Lw = norm(Lw,1);%SOR法矩阵范数
    vrho_Lw = max(abs(eig(Lw)));%SOR法谱半径


%     fprintf('SOR法矩阵范数：%16.15f\n',norm(Lw,1));
%     fprintf('SOR法谱半径：%16.15f\n',max(abs(eig(Lw))));
%     fprintf('SOR法松弛因子：%16.15f\n',w);

    fw = w*((D-w*L)\b);
    x = x0;
    while norm(delta_x,inf)>tol
        x_last = x;
        x = Lw*x_last + fw;
        times = times+1;
        delta_x = x - x_last;
    end
    final_delta_x = norm(delta_x,inf);
end

可以发现：

• SOR法在维数$n<12$时，谱半径小于1，SOR法迭代收敛，误差较小；
• 随着维数$n$增大，谱半径显示为1，可能是MATLAB已经出现舍入误差，计算结果的误差虽然不断增大但仍可接受；
• 相比于GS法，SOR法能显著减少达到收敛需要的迭代次数，提高了计算的效率，但计算结构误差略大；
• 取得最少迭代次数的松弛因子不断变化。

说明对于Hilbert矩阵为系数矩阵的病态方程，SOR法可以收敛，并且所需迭代次数较少，但缺点在于需要合理的选取松弛因子以减少迭代次数，并获得正确的计算结果。