【记忆增强深度条件展开网络】
Memory-augmented Deep Conditional Unfolding Network for Pan-sharpening
(面向全色锐化的记忆增强深度条件展开网络)
全色锐化旨在为遥感系统获取高分辨率的多光谱图像,基于深度学习的方法已经取得了显著的成功。然而,大多数现有的方法是在黑盒原理下设计的,缺乏足够的可解释性。另外,它们忽略了MS图像各波段的不同特征,直接将其与全色(PAN)图像拼接,导致严重的复制伪影。针对上述问题,提出了一种可解释的深度神经网络,即具有两种特定核心设计的记忆增强深度条件展开网络。首先,考虑图像的退化过程,将全色锐化问题转化为一个变分模型的最小化问题,该变分模型具有基于去噪的先验知识和非局部自回归先验知识,能够搜索长距离块之间的相似性,有利于纹理增强,提出了一种新的基于神经网络的迭代算法用于透明模型设计。其次,为了充分挖掘MS图像不同波段的潜力,将PAN图像与MS图像的各个波段相结合,有选择地提供高频细节,减轻复制伪影。
介绍
随着遥感器的快速发展,越来越多的卫星图像可用于诸如测绘服务、军事系统和环境监测等广泛的应用。卫星同时捕获多光谱(MS)和全色(PAN)图像,并且对于每种模态具有互补信息,即PAN图像具有高空间解,而MS图像包含丰富的光谱信息。为了获得高光谱和空间分辨率的图像,旨在融合MS和PAN图像的全色锐化技术已经引起了越来越多的关注。
在过去的几十年里,全色锐化领域的研究工作呈爆炸式增长,其中的重点包括基于模型和基于深度学习(DL)的方法。由于全色锐化的病态性,前者通常需要人工构造先验知识来正则化潜在的高分辨率MS图像的解空间。然而,手工制作的先验概率的表示能力有限导致不满意的性能在处理复杂的场景。此外,传统的优化方法是具有挑战性的,限制了其实际应用。灵感来自深层神经网络的成功,各种基于DL的Pan-sharpening算法已经提出。尽管现有的基于DL的全色锐化方法在特征表示和模型泛化方面表现出了优越性,但它们长期以来存在的一个问题是缺乏可解释性,因为它们大多数是在黑箱原则下设计的,没有考虑模型的合理性。因此,将领域知识与可解释的基于DL的模型相结合有望提高全色锐化性能。另外,现有的方法忽略了MS图像各波段的不同特征,直接将其与PAN图像沿着通道方向拼接,会导致严重的复制伪影。
最近,一些模型试图在图像处理社区中结合基于模型和基于DL的方法的优点。受此启发,Xu等人提出了第一个用于全色锐化的深度展开网络。它将全色锐化公式化为两个单独的优化问题,通过深度先验对PAN和低分辨率(LR)MS图像进行正则化。然而,设计的内隐先验仍然难以彻底考察其影响,跨阶段的潜力尚未得到充分挖掘。
总之,现有技术水平(SOTA)方法遭受两重问题:1)缺乏足够的可解释性,和2)忽略MS图像的每个带的不同特征。为此,结合基于模型和数据驱动的深度展开方法的优点,提出了一种可解释的深度展开网络,即记忆增强的深度条件展开网络(Memory augmented Deep Conditional Unfolding Network,MDCUN)。考虑到MS图像的退化过程,并考虑到MS图像经常包含重复结构,我们将全色锐化问题描述为一个变分模型的最小化问题,该变分模型具有两个新设计的先验项,包括基于去噪的先验项和非局部自回归先验项。前者旨在重建潜在的MS图像,后者学习长距离块之间的相似性,有利于纹理增强和减少混叠伪影。然后,利用一种新的有效的迭代算法和内置的神经网络进行透明模型设计,以进一步提高模型的可解释性。此外,为了充分挖掘MS图像不同波段的潜力,我们提出了一种波段感知PAN引导的高频信息提取模块。具体地,PAN图像与MS图像的每个带组合,选择性地提供高频细节并减轻复制伪影。此外,引入上下文记忆机制,增强了迭代阶段的容量,从而促进了信息交互。通过大量的实验验证了该方法的有效性,实验结果定性和定量地证明了该方法的优越性。
贡献
1)我们将全色锐化表示为变分模型的最小化,并在改进长距离相干性之前引入了基于去噪的先验和非局部自回归。
2)本文提出了一种可解释的深度网络,即记忆增强的深度条件展开网络,该网络综合了基于模型和数据驱动的深度条件展开方法的优点。
3)设计了一种波段感知PAN引导的高频信息提取模块,充分挖掘MS图像不同波段的潜力。此外,还引入了上下文记忆机制,以增加迭代阶段的容量,促进信息交互。
4)在不同卫星数据集上的大量实验表明,该方法以较少的参数优于现有算法。
相关工作
Classic pan-sharpening methods
经典的全色锐化方法可以分为三大类,包括分量替换(CS)、多分辨率分析(MRA)和变分优化(VO)。常见的CS方法通过特定的变换从MS图像中分离空间和光谱信息,然后用PAN图像替换分离的空间分量。典型的MRA方法补充了通过多分辨率分解技术从PAN图像提取的高频细节到上采样MS图像。VO方法因其对全色锐化的精细融合效果而备受关注。他们假设HR MS和PAN图像之间存在一定的约束或先验条件,并基于所提出的条件建立特定的优化函数,从而通过优化上述问题来很好地平衡光谱和空间质量。
Deep learning based methods
PNN利用卷积神经网络的高度非线性映射能力,使用三个卷积单元映射PAN、LR MS和HR MS图像之间的关系,与其他经典方法相比,这实现了显著的改进。受概率神经网络的启发,近年来出现了大量基于离散元的全色锐化研究。如PANNet采用了ResNet中的残差学习模块,MSDCNN 在残差连接的基础上增加了多尺度模块,SRPPNN参考了SRCNN的设计思想。观察到MS和PAN中的相同对象并不总是对准的,Li等人设计了具有特征对准模块的SIPSA-Net,该特征对准模块可以对准来自PAN和LR MS图像的特征。Wu等人利用多个并行分支将不同规模的特征集成到骨干网络中以提高性能。针对卫星图像分析,Ma等人提出了一种基于生成式对抗网络的无监督框架。此外,一些模型驱动的CNN模型出现了,如MHNet和GPPNN,这些模型类似于我们的工作,具有明确的物理意义。
Deep unfolding network
深度展开网络
深度展开网络
近年来,许多研究者尝试将领域知识与深度神经网络相结合,提出深度展开网络,利用基于模型方法的可解释性和基于学习方法的强映射能力。具体而言,深度展开网络首先将某些优化算法展开并利用深度神经网络对展开模型进行参数化,然后在大训练数据集上最小化损失函数,并以端到端的方式对参数进行优化。例如,Zhang等人将迭代收缩阈值算法转换为深度网络形式,用于图像压缩感知。为了有效解决JPEG压缩伪影去除问题,Fu等人设计了一种交替最小化算法,并将其展开到深度网络架构中。此外,深度展开网络还被提出用于图像超分辨率、图像去模糊、快照压缩感测和图像去马赛克。
方法
本文将全色锐化问题描述为一个由全色引导的MS超分辨率问题,全色锐化过程可表示为L = DKH + eh,其中,L表示通过对HR MS版本H分别执行K和D矩阵的模糊和下采样的LR MS图像,eh表示噪声。参考上述观察模型,通过求解最小化问题可以获得HR MS图像:

其中P表示PAN图像,并提供用于恢复HR MS图像H的补充信息。η是拉格朗日乘子,Ω(H,P)描述正则化函数。
基于遥感图像中含有丰富重复结构的特点,利用非局部自回归先验模型(NARM)得到的图像先验(N先验)约束上述优化。给定MS块,NARM在一组非局部(而不是局部)邻域上寻求其稀疏线性分解。NARM可表示为:

通过引入上述NARM,观测模型被改写为:

其中n = dk是一个新的建模错误。因此,Eq.1的最小化问题被改写为:

Optimization
在半二次分裂(HQS)的框架下,分别为H和SH引入两个辅助参数U和V,Eq.4可以公式化为无约束优化问题:

其中η1、η2、λ 1和λ2为罚参数。为了获得展开推理,Eq.5的问题可以分为以下三个子问题并交替求解:
此外,我们使用邻近梯度投影法来解决上述三个子问题:
其中,proΩ1(·)和proΩ2(·)是对应于罚值Ω1(·)和Ω2(·)的近端算子。与梯度相关的符号详述如下:
Deep unfolding network

受模型驱动深度学习原理的启发,我们的深度展开网络包含K个阶段,这些阶段专门设计为与优化算法中的K次迭代相对应,如图2所示。在每个网络中,首先更新两个辅助变量(U和V),然后计算恢复图像来更新存储组件(UM emory和VM emory)。为了构造一个逐步对应的深度展开网络结构,我们将上述迭代步骤推广为特定的网络模块,包括PAN指导的条件带通MS去噪模块、非局部自回归先验模块、记忆增强信息模块和重构模块。
在图2中,HQS的第k次迭代被投射到模型的第k阶段,该阶段包括去噪模块(DM)、NARM模块和重建模块,如下所示:
其中Down和Up分别表示空间分辨率中的下采样和上采样函数。DM和NARM分别表示去噪模块和非局部自回归先验模块。此外,可以注意到,每个去噪阶段涉及PAN图像,同时取决于先前状态。当然,去噪模块的设计需要考虑存储机制和条件服务PAN图像。具体而言,在检查第k阶段时,PAN引导模块负责更新两个辅助变量 U ( k ) U^{(k)} U(k)和 V ( k ) V^{(k)} V(k),而非局部自回归先验模块旨在计算NARM矩阵S以更新对应的 S H ( K ) SH^{(K)} SH(K)。存储器扩充信息模块获取输出 U ( 0 ) U^{(0)} U(0),…, U ( k − 1 ) U^{(k-1)} U(k−1)和 V ( 0 ) V^{(0)} V(0),…, V ( k − 1 ) V^{(k-1)} V(k−1)个去噪模块作为跨远程阶段的输入,以促进信息流动。重建模块对应于Eq.18来更新所恢复的 H ( K ) H^{(K)} H(K)。更新的 H ( K ) H^{(K)} H(K)被馈送到下一级,并且执行重复操作,直到级数达到K。接下来我们将详细介绍每个模块。
Non-local auto-regressive prior module
正如上文谈到的,NARM在一组非局部邻域上寻求稀疏线性分解。像素Hi可以由其非局部邻居(包括其自身)近似加权:
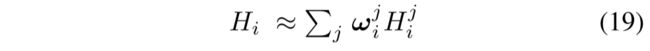
其中 H j H^j Hji表示Hi的第j个非局部邻居。并且 w j w^j wji通过以下优化问题求解:

基于确定的系数ωi,推导出Eq.2中NARM矩阵S的公式表示为:
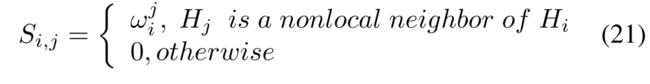
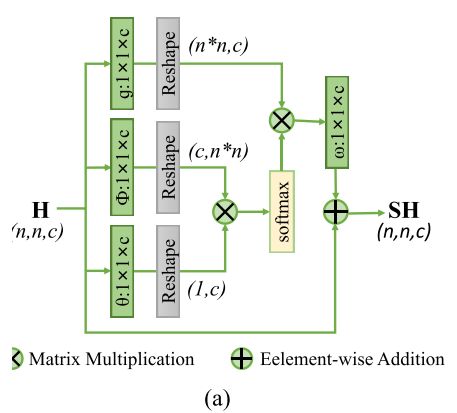
可以通过非本地网络实现计算Eq.2中的非局部邻居之间的相似性。NARM(SH)的输出表示为:
其中,相似性函数f(·,·)计算Hi和Hj之间的关系。NARM的体系结构如图3(a)所示。
PAN-guided band-aware MS denoise module
对于MS图像增强问题,有效地利用高通PAN图像与不同波段MS图像各波段之间的内在联系是至关重要的。如图3(b)所示,我们引入高通修正块学习高通信息,利用高通信息增强MS中各波段的空间信息,从而达到去噪的目的。

利用第k级网络 H ( K ) H^{(K)} H(K)的输出和NARM S H ( K ) SH^{(K)} SH(K)的输出,我们考虑D先验和N先验,并将PAN图像作为Eq.4中的条件。
PAN指导的频带感知MS去噪模块可由Eq.6和Eq.7指导的去噪模块(DM)来实现。Eq.6和Eq.7其中前一级DM( U ( k − 1 ) U^{(k-1)} U(k−1)或 V ( k − 1 ) V^{(k-1)} V(k−1))的输出、 H ( K ) H^{(K)} H(K)和条件P用作MDCUN的第k级的输入,如Eq.15和Eq.17所示
Memory-augmented information module
本文考虑到方程中的记忆信息,Eq.15和Eq.17充分利用模型产生的记忆信息,引入记忆组件来存储记忆信息并保持记忆信息的更新。记忆组件主要储存两种先验的记忆信息。
如图2所示,在PAN导引的带感知MS去噪模块的第k级输入中,前一级DM的输出( U ( k − 1 ) U^{(k-1)} U(k−1)和 V ( k − 1 ) V^{(k-1)} V(k−1))将被记忆成分(UM emory和VM emory)代替,因此DM的输入为记忆成分 H ( K ) H^{(K)} H(K)和条件P,因此我们有:
将PAN引导的带感知MS去噪模块的输出 U ( k ) U^{(k)} U(k)和 V ( k ) V^{(k)} V(k)分别输入到两个不同的存储部件中,完成存储部件中存储信息的更新。在第k级,考虑PAN引导的频带感知MS去噪模块的两个输出 U ( k ) U^{(k)} U(k)和 V ( k ) V^{(k)} V(k),UM emory中的元素为{ U ( 0 ) U^{(0)} U(0),…, U ( k − 1 ) U^{(k-1)} U(k−1)},并且V存储器中的元素是{ V ( 0 ) V^{(0)} V(0),…, V ( k − 1 ) V^{(k-1)} V(k−1)}。
Reconstruction module
利用 H ( k ) H^{(k)} H(k)、 S H k SH^k SHk、 U k U^k Uk和 V k V^k Vk,我们可以根据Eq.11和Eq.14迭代地重构 H ( k + 1 ) H^{(k+1)} H(k+1)的值。分别使用卷积网络层来模拟算子(DK ) T )^T )T和DK。具体而言,DK通过网络调用降采样块(Down)进行模拟,降采样块由3×3核和64个通道的卷积层、降低空间分辨率的maxpool层和两个3 × 3核的卷积层组成,用于重新投影到原始维度,如图3(c)所示。
类似地,(DK ) T )^T )T由一个称为上采样块(Up)的网络模拟,该网络由一个具有3 × 3内核和64个通道的卷积层、一个用于增加空间分辨率的上采样层和两个具有3×3内核的卷积层组成,用于重新投影到原始维度,如图3(d)所示。