2019 ICLR | Learning Multimodal Graph-to-Graph Translation for Molecular Optimization

Paper: https://arxiv.org/pdf/1812.01070
Code: https://github.com/wengong-jin/iclr19-graph2graph

2019 ICLR | Learning Multimodal Graph-to-Graph Translation for Molecular Optimization

作者把分子优化看作是一个图到图的平移问题。目标是学习从一个分子图映射到另一个更好的适当关系，基于配对分子可用的语料库。由于分子可以通过不同的方式进行优化，因此每个输入图都有多种可行的平移。由于分子可以通过不同的方式进行优化，因此每个输入图都有多种可行的平移。因此，一个关键的挑战是建模各种翻译输出。因此模型包括一个连接树编码器-解码器，用于学习不同的图平移，以及一种新的对抗性训练方法，以对准分子的分布。而不同的输出分布是通过调节平移过程的低维潜在向量显式实现的。实验表明，在多个分子优化任务上， 该模型优于之前最先进的基线。

模型

翻译模型将接线树变分自动编码器扩展到用于学习图形映射的编码器架构。根据他们的工作，将每个分子解释为从有效的化学子结构词汇表中选择子图(原子簇)构建而成。这些簇形成一个连接树，代表分子的支架结构(图1)，这是药物设计中的一个重要因素。这种从粗到细的方法允许轻松地加强生成的图形的化学有效性，并提供了一个丰富的表示，在不同的尺度上编码分子。

在模型架构上，编码器是一个图消息传递网络，将树中的节点和图中的节点都嵌入到连续的向量中。该解码器由一个用于预测连接树的树结构解码器和一个学习将预测连接树中的簇组合成分子的图解码器组成。与Jin等人主要区别包括树和图的统一编码器架构，以及树解码过程中的注意机制。

树和图形编码器

将树视为图，使用图消息传递网络对连接树和图进行编码。具体而言，图定义为$G=(\epsilon ,\upsilon )$，其中$\epsilon$是顶点集和$\upsilon$边缘集。

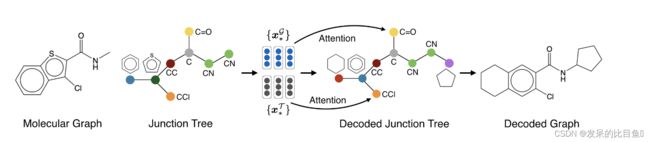
图1:编码器-解码器模型示意图。分子由它们的图结构和编码分子支架的连接树表示。连接树中的节点(称之为簇)是有效的化学子结构，如环和键。在解码过程中，模型首先生成连接树，然后将预测树中的簇组合成一个分子。

每个节点$\epsilon$都有一个特征向量$f_v$。对于原子，它包括原子类型、价态和其他原子性质。对于连接树中的集群，$f_v$是一个热点向量，表示其集群标签。同理，每条边$(\mu ,\upsilon )\in \epsilon$都有一个特征向量$f_{\mu \upsilon }$。设$N(\upsilon )$是$\upsilon$的邻居节点的集合。每条边$(\mu ,\upsilon )$都有两个隐藏向量$v_{\mu \upsilon }$和$v_{\upsilon \mu }$，它们代表了从$\mu$到$\upsilon$的信息，反之亦然。这些消息通过神经网络$g_1(\cdot )$迭代更新:

其中${\nu }_{uv}^{(t)}$是在第$t$次迭代中计算的消息，用${\nu }_{uv}^{(0)}=0$初始化。在每次迭代中，所有消息都是异步更新的，因为节点之间没有自然的顺序。这与Jin等人(2018)的树编码算法不同，后者指定了一个根节点，并对消息更新施加了人为的顺序。移除这个伪影是必要的，因为学习到的嵌入会因人为的顺序而产生偏差。

经过$T$步迭代后，通过另一个神经网络$g_2(\cdot )$聚合消息，得出每个顶点的潜在向量，捕捉其局部图(或树)结构:

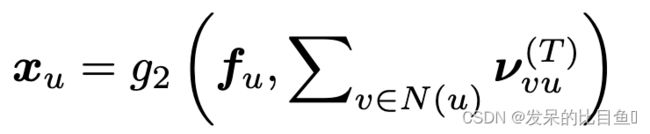
将上述消息传递网络应用于连接树$T$和图$G$，得到两个向量集$\{x_1^T，\cdot \cdot \cdot ，x_n^T\}$和$\{x_1^G,\cdot \cdot \cdot ,x_n^G\}$。树向量$x_i^T$是树节点$i$的嵌入，图向量$x_j^G$是图节点$j$的嵌入。

联合树解码器

利用带有注意机制的树递归神经网络生成一棵$T=(\epsilon ,\upsilon )$的连接树。这棵树是通过一次扩展一个节点来以自上而下的方式构造的。信息$h_{i_t,j_t}$通过树门控循环单元更新。

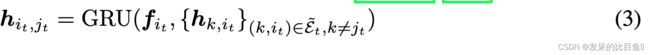
Topological Prediction 当模型访问节点$i_t$时，首先通过一个隐层网络，结合节点特征KaTeX parse error: Double subscript at position 4: f_i_̲t拟合和内部消息$h\{k,i_t\}$，计算出一个预测隐状态$h_t$。然后，该模型对是否展开一个新节点或回溯到$i_t$的父节点进行二进制预测。概率的计算方法是将源编码$\{x_{\ast }^T\}$和$\{x_{\ast }^G\}$通过一个注意层进行聚合，然后是一个前馈网络($\tau (\cdot )$表示ReLU， $\sigma (\cdot )$表示sigmoid):

attention$(\cdot ;(U_{att}^d)$表示带有参数的注意机制。输出$c_t^d$是树和图注意向量的串联:

Label Prediction 如果节点$j_t$是一个从父节点$i_t$生成的新子节点:

图解码器

解码过程的第二步是根据预测的连接树$T$构造分子图$G$，这一步是不确定的，因为多个分子可能对应同一棵连接树。例如上图中的连接树可以组装成三个不同的分子。

图解码器训练为最大限度地提高所有树节点的地面真值子图的对数似然。在训练过程中，采用教师强迫的方式，以地真连接树为输入输入图形解码器。在测试过程中，按照连接树解码的顺序，一次组装一个邻域。

多模式图形翻译

目标是学习两个分子域之间的多模态映射，例如低溶解度分子和高溶解度分子，或强效分子和弱效分子。

变分交界树编码器（VJTNN）

训练目标遵循一个条件变分自编码器，包括一个重建损失和一个KL正则项：

下图是整个的算法流程：

数据：

未知

评价指标

• Penalized logP
• QED
• Dopamine Receptor (DRD2)

baseline

• MMPA
• Junction Tree VAE
• VSeq2Seq
• GCPN