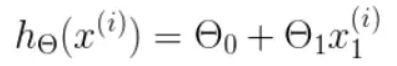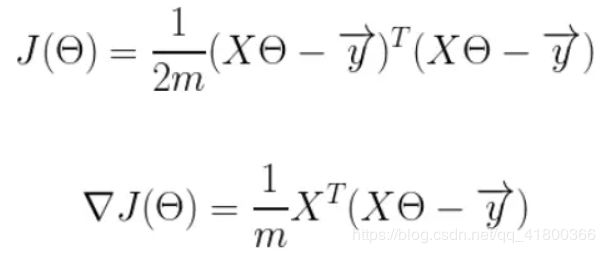机器学习之梯度下降法详解

---

一、数学基础

1.1 一元函数的导数

在微积分中，函数$f(x)$在点$x_0$处的导数定义为：$f^{\prime }(x)=\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}$，在几何上就是指$f(x)$在$x_0$上的切线方向。

一般而言，计算函数$f(x)$的最值，会令其导数为0，求解方程$f^{\prime }(x)=0$，这么做可以得到函数的临界点，进一步判断是否最大或者最小。但是这不是最值得充要条件。这个临界点不一定是全局最大或者最小，也不一定是局部最大或者最小。比如函数$f(x)=x^3$，导数为0的点是$x=0$，这个点既不是局部最大也不是局部最小。

1.2 多元函数的偏导数和梯度

例如，对于多元函数$f(x)=f(x_1,...,x_n)$来说，它的梯度可以定义为：

$\nabla f(x)=(\frac{\partial f}{\partial x_1}(x),...,\frac{\partial f}{\partial x_n}(x))$

实际上，梯度就是多元微分的一般化。
举个例子来说，对于函数$f(x)=0.5+5x_1-2x_2+11x_3$来说，它的梯度为：

$\nabla f(x)=⟨\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}⟩=⟨5,-2,11⟩$

从上面看出，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用$<>$包括起来，说明梯度其实一个向量。

• 在一元函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
• 在多元函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。

即，从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。如果想计算一个函数的最小值，就可以使用梯度下降法的思想来做。

二、梯度下降法

2.1 简介

一句话概括，梯度下降法就是一种寻找目标函数最小化的方法。

2.2 算法介绍

2.2.1 场景假设

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了。

2.2.2 梯度下降语言描述

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数变化最快的方向(数学基础中已经解释过)

所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点！

2.2.3 梯度下降数学解释

首先给出数学公式：

${\Theta }^1={\Theta }^0-\alpha \nabla J(\Theta )$

此公式的意义是：$J$是关于$\Theta$的一个函数，我们当前所处的位置为${\Theta }_0$点，要从这个点走到 $J$ 的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是$\alpha$，走完这个段步长，就到达了${\Theta }_1$这个点！

（1）步长$\alpha$：

$\alpha$ 在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过 $\alpha$来控制每一步走的距离。$\alpha$ 不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

（2）梯度要乘以一个负号

梯度前加一个负号，就意味着朝着梯度相反的方向前进。我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向，而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号；那么如果时上坡，也就是梯度上升算法，当然就不需要添加负号了。

2.3 实例

我们已经基本了解了梯度下降算法的计算过程，那么我们就来看几个梯度下降算法的小实例。

2.3.1 一元函数的梯度下降

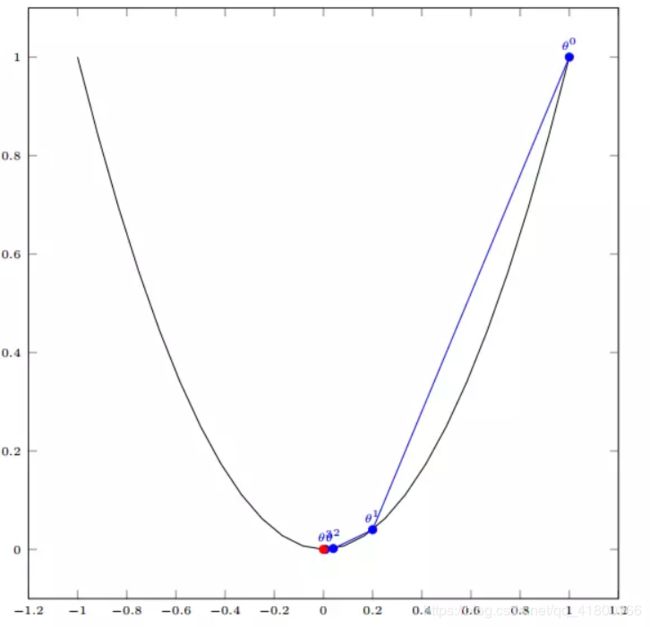
我们假设有一个单变量的函数$f(x)=x^2$，函数微分为$f^{\prime }(x)=2x$；

初始化起点假设为：$x^0=1$，学习设置为$0.4$，根据梯度下降的公式：${\Theta }^1={\Theta }^0-\alpha \nabla J(\Theta )$，我们计算梯度下降的迭代计算过程为：

$\begin{array}{l}{x}^0=1\\ x^1=x^0-\alpha \ast f^{\prime }(x^0)=1-0.4\ast 2\ast 1=0.2\\ x^2=x^1-\alpha \ast f^{\prime }(x^1)=0.2-0.4\ast 2\ast 0.2=0.04\\ x^3=x^2-\alpha \ast f^{\prime }(x^2)=0.008\\ x^4=x^3-\alpha \ast f^{\prime }(x^3)=0.0016\end{array}$

如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底

2.3.2 多元函数的梯度下降

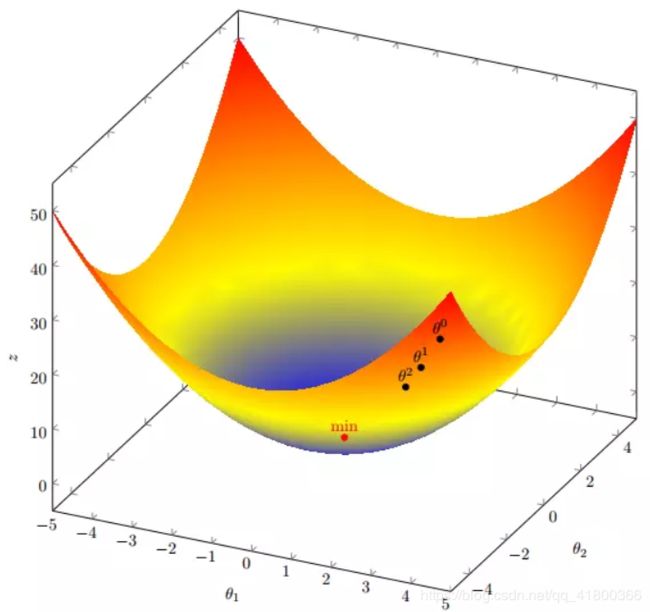
我们假设有一个目标函数：$f(x)=x_1^2+x_2^2$

假设初始起点为：$X^0=(1，3)$，初始学习率为：$\alpha =0.1$，函数的梯度为：$\nabla f(X)=⟨2x_1,2x_2⟩$

进行多次迭代：

$\begin{array}{l}{X}^0=(1,3)\\ X^1=X^0-\alpha \ast \nabla f(X^0)=(1,3)-0.1\ast (2,6)=(0.8,2.4)\\ X^2=X^1-\alpha \ast \nabla f(X^1)=(0.61,1.92)\\ X^3=(0.512,1.536)\\ ......\\ X^{10}=(0.1074,0.3221)\\ ......\\ X^{50}=(1.1418e^{-05},3.4254e^{-05})\\ ......\\ X^{100}=(1.1629e^{-10},4.8888e^{-10})\end{array}$

我们发现，已经基本靠近函数的最小值点$(0,0)$

2.4. 代码实战

2.4.1 例1：使用梯度下降求函数 $f(x,y)=x^2+y^2$ 的最小值。

首先求得函数的梯度：

def get_gradient(x, y):
    return 2*x, 2*y

然后迭代：

def gradient_descent():
    x, y = 5, 5   #起始位置
    alpha = 0.01
    epsilon = 0.3
    grad = get_gradient(x, y)
    while x**2+y**2 > epsilon**2:
        x -= alpha*grad[0]     # 沿梯度方向下降
        y -= alpha*grad[1]
    
    print("({},{})取值为{}".format(x, y, x**2+y**2) )

最后的结果：

(0.20000000000000104,0.20000000000000104)取值为0.08000000000000083

真实最小值在(0,0)点取得，最小值为0，两者非常接近（上面的epsilon设置的比较大，当epsilon很小时，最后的结果会非常接近0）。

2.4.2 例2：用梯度下降法来拟合直线【线性回归】

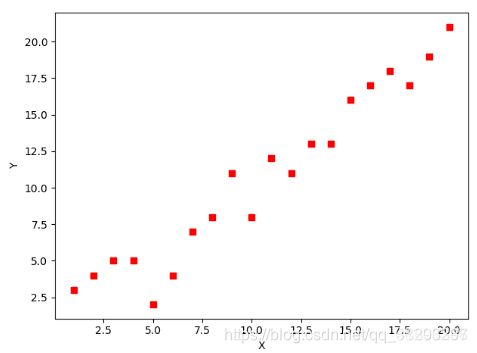
假设有如下一系列点，如何用梯度下降法拟合出这条直线？

分析：可以定义一个代价函数，代价函数包括一个预测函数(预测值：$y^{\prime }=ax+b$)，预测函数含有待求解的直线方程的两个参数。通过梯度下降法求解这个函数的最小值得到参数。

首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数（也称平方误差代价函数）

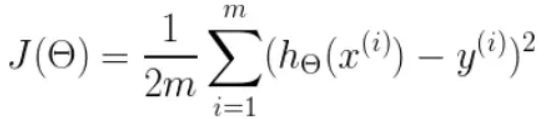
• $m$是数据集中数据点的个数，也就是样本数
• $½$ 是一个常量，这样是为了在求梯度的时候，二次方乘下来的$2$就和这里的 $½$ 抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
• $y$是数据集中每个点的真实 $y$ 坐标的值，也就是类标签
• $h$ 是我们的预测函数（假设函数），根据每一个输入 $x$，根据 $\Theta$ 计算得到预测的 $y$ 值，即
  

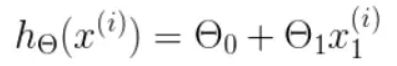
我们可以根据代价函数看到，代价函数中的变量有两个，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分，即：

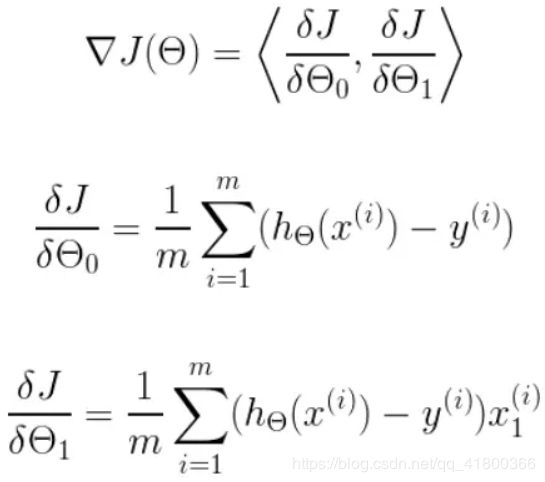
明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。

但在这之前，需要说明一点，就是为了方便代码的编写，我们会将所有的公式都转换为矩阵的形式，python中计算矩阵是非常方便的，同时代码也会变得非常的简洁。

为了转换为矩阵的计算，我们观察到预测函数的形式

我们有两个变量，为了对这个公式进行矩阵化，我们可以给每一个点 $x$ 增加一维，这一维的值固定为 $1$，这一维将会乘到${\Theta }_0$ 上。这样就方便我们统一矩阵化的计算：

然后我们将代价函数和梯度转化为矩阵向量相乘的形式：

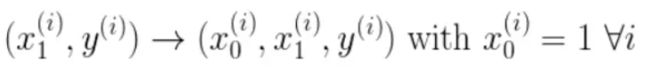
代码如下：
（1）. 首先，我们需要定义数据集和学习率

from numpy import *

# 数据集大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1))  # 生成一个m行1列的向量，也就是x0，全是1
X1 = arange(1, m+1).reshape(m, 1)  # 生成一个m行1列的向量，也就是x1，从1到m
X = hstack((X0, X1))  # 按照列堆叠形成数组，其实就是样本数据
# 对应的y坐标
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01

（2）. 接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度

# 定义代价函数
def cost_function(theta, X, Y):
    diff = dot(X, theta) - Y  # dot() 数组需要像矩阵那样相乘，就需要用到dot()
    return (1/(2*m)) * dot(diff.transpose(), diff)


# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
    diff = dot(X, theta) - Y
    return (1/m) * dot(X.transpose(), diff)

（3）. 最后就是算法的核心部分，梯度下降迭代计算

# 梯度下降迭代
def gradient_descent(X, Y, alpha):
    theta = array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, Y)
    while not all(abs(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, Y)
    return theta


optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])

当梯度小于1e-5时，说明已经进入了比较平滑的状态，类似于山谷的状态，这时候再继续迭代效果也不大了，所以这个时候可以退出循环！

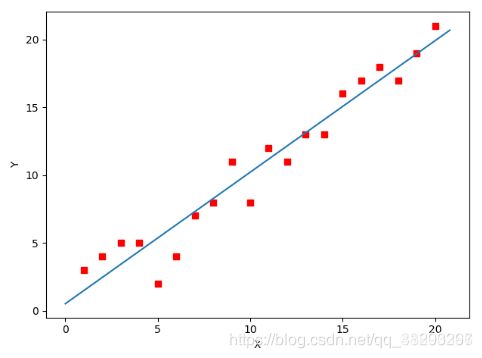
（4）. 运行代码，计算得到的结果如下：

print('optimal:', optimal)  # 结果 [[0.51583286][0.96992163]]
print('cost function:', cost_function(optimal, X, Y)[0][0])  # 1.014962406233101

（5）. 通过matplotlib画出图像

# 根据数据画出对应的图像
def plot(X, Y, theta):
    import matplotlib.pyplot as plt
    ax = plt.subplot(111)  # 这是我改的
    ax.scatter(X, Y, s=30, c="red", marker="s")
    plt.xlabel("X")
    plt.ylabel("Y")
    x = arange(0, 21, 0.2)  # x的范围
    y = theta[0] + theta[1]*x
    ax.plot(x, y)
    plt.show()


plot(X1, Y, optimal)

所拟合出的直线如下

三、梯度下降分类

以线性回归为例，假设训练集为$T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$，其中$x_i\in R^n$是一个向量，$y_i\in R$。

我们通过学习得到了一个模型 $f_M(x,w)={\sum }_{j=0}^M{w}_i{x}^i$，可以根据输入值 $x$ 来预测 $y$， 预测值和真实值之间会有一定的误差，我们用均方误差(Mean Squared Error) MSE来表示：

$L(w)=\frac{1}{2N}{\sum }_{i=1}^N{(f_M(x_i,w)-y)}^2$

$L(w)$ 被称为损失函数（loss function），加 $1/2$ 的目的是为了计算方便， $w$ 是一个参数向量。

根据梯度下降时使用数据量的不同，梯度下降可以分为3类：批量梯度下降（Batch Gradient Descent，BGD）、随机梯度下降（Stochastic Gradient Descent， SGD）和小批量梯度下降（Mini-Batch Gradient Descent, MBGD）。

3.1 批量梯度下降（Batch Gradient Descent，BGD）

批量梯度下降每次都使用训练集中的所有样本来更新参数，也就是

$L(w)=\frac{1}{2N}{\sum }_{i=1}^N{(f_M(x_i,w)-y)}^2$

更新方法为

$w^{(k+1)}=w^{(k)}-\alpha \ast \frac{\partial L(w)}{\partial w}$

当样本数据集很大时，批量梯度下降的速度就会非常慢。

优点：可以得到全局最优解
缺点：训练时间长

3.2 随机梯度下降（Stochastic Gradient Descent， SGD）

每次梯度下降过程都使用全部的样本数据可能会造成训练过慢，随机梯度下降（SGD）每次只从样本中选择1组数据进行梯度下降，这样经过足够多的迭代次数，SGD也可以发挥作用，但过程会非常杂乱。“随机”的含义是每次从全部数据中中随机抽取一个样本。这样损失函数就变为：

$L(w)=\frac{1}{2}{(f_M(x,w)-y)}^2$

参数更新方法同上：

$w^{(k+1)}=w^{(k)}-\alpha \ast \frac{\partial L(w)}{\partial w}$

优点：训练速度快
缺点：准确度下降，得到的可能只是局部最优解

3.3 小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

小批量梯度下降是 BGD 和 SGD 之间的折中，MBGD 通常包含 10-1000 个随机选择的样本。MBGD降低了了SGD训练过程的杂乱程度，同时也保证了速度。

（例子可以参见博客：https://www.cnblogs.com/sench/p/9817188.html）

四、参考

1. https://blog.csdn.net/qq_41800366/article/details/86583789
2. https://www.zhihu.com/question/305638940
3. https://www.cnblogs.com/sench/p/9817188.html