【Graph Embedding】LINE:算法学习笔记
Large-scale Information Network Embedding(LINE)算法
本文是本人在学习LINE算法中参考各路大神博客所做的一个学习笔记
文中夹杂了一些个人理解,如有不到位之处欢迎指正讨论。
文章欢迎转载,请标明出处,谢谢。
1.网络结构
在现实网络结构当中,如果节点之间有相连接的边,则认为两个节点具有一定的相似性,如果这又是个带权的网络结构,则可以用节点与节点之间相连接的边的权重来度量两个节点之间的相似性。这种节点与节点之间的相似性度量方式在LINE算法中定义为一阶近邻。如下图所示的(1,5),(2,6)
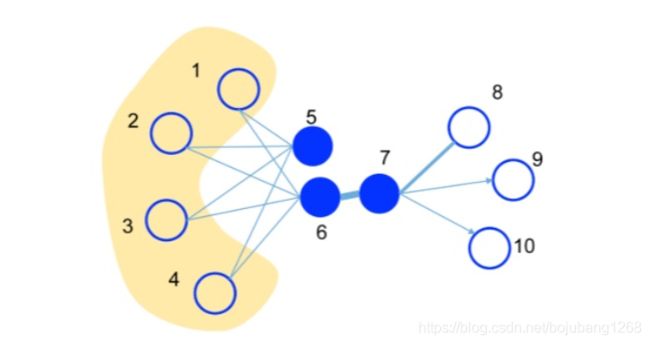
但在现实网络结构当中,仅仅用一阶近邻来度量两个节点似乎并不准确,比如上图所示节点(5,6),虽然节点5与节点6之间不存在直接相连的边,但他们之间有共有的邻居,节点(1,2,3,4)。原文作者对于这种情况的出现,定义了一种二阶近邻,即通过判断两个节点之间的共有邻居来度量两个节点之间的相似度。
2.表达公式
2.1.一阶近邻
一阶近邻用到的公式如下所示:
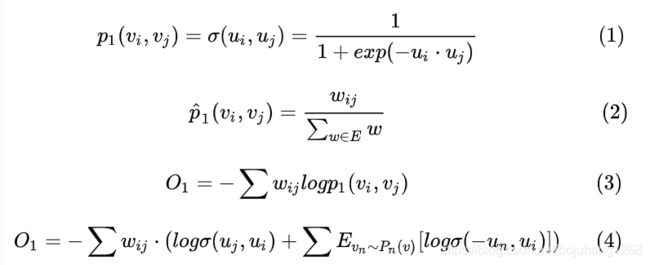
我们假设 V 为图中的所有节点集合, V i V_{i} Vi, V j V_{j} Vj为我们想要求相似度的两个顶点, w i j w_{ij} wij为顶点 V i V_{i} Vi与 V j V_{j} Vj之间的连接边权重, u i u_{i} ui, u j u_{j} uj为节点 V i V_{i} Vi, V j V_{j} Vj的embedding向量。
由我们上述一阶相似度的定义可知,节点 V i V_{i} Vi与 V j V_{j} Vj之间的相似度可以由 w i j w_{ij} wij来进行表示,所以我们可以用经验概率分布公式(2),得到 w i j w_{ij} wij在整个w(边权之和)当中的占比,进而衡量 w i j w_{ij} wij的重要程度(也就是概率)
u i u_{i} ui, u j u_{j} uj为节点 V i V_{i} Vi, V j V_{j} Vj的embedding向量,两个向量之间的相似度可以用( u i u_{i} ui. u j u_{j} uj)的点乘进行表示,在此基础上套上一个sigmoid函数,将其映射到0~1之间,也就变成了一个概率分布,由公式(1)所示
由此问题就转换成了度量公式(1),(2)两个分布之间的距离问题,只要我们能够使得
它们之间距离越来越近,就能得到我们想要的embedding向量
度量两个分布之间的距离最常用的方式就是KL散度,最终的优化目标函数如公式(3)所示,这里是作者省去了常数项之后的最终结果,有关KL散度怎么省去常数项的问题可以参考下面这个博客。
https://www.cnblogs.com/ymjyqsx/p/7085931.html
不过,公式(3)中缺乏负样本的存在,仅仅优化正样本会导致部分向量非常大,这种情况可以通过引入负样本来进行解决,引入的方式借鉴了word2vec中的Negative sampling方法,最终目标函数如公式(4)所示。
Negative sampling 负采样方法可以参考博客https://www.cnblogs.com/pinard/p/7249903.html
从公式中可以看出,一阶近邻没有考虑方向的问题,因此只能用于无向图当中。
2.2.二阶近邻
二阶近邻公式如下所示
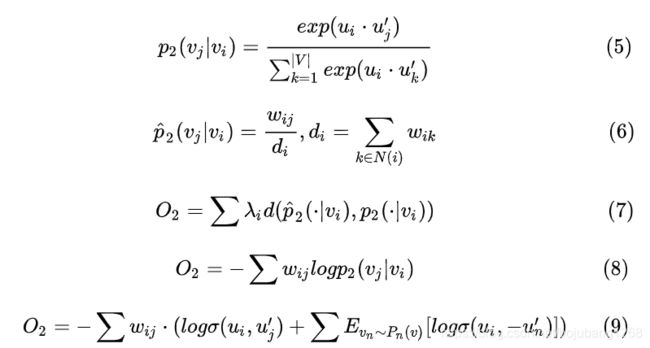
和一阶近邻一样,我们首先定义一个经验概率分布,如公式(6)所示,其中 w i j w_{ij} wij为两个节点之间边的权重,k为节点的出度数量, d i d_{i} di为节点出度节点边的权重之和。也就是说公式(6)度量了两个节点之间的边权占目标节点出度节点
(也就是邻居) 的边权之和的占比。
二阶近邻描述的是节点与邻域的关系,每个节点有两个角色,一个表示节点本身,另一个表示其他节点的邻居,因此文中对每个节点定义了两个大小相等但意义不一样的embedding向量。 u i u_{i} ui表示节点 v i v_{i} vi作为节点本身的embedding向量,(此处的含义与一阶近邻中的 u i u_{i} ui一致)。 u i ′ u^{'}_{i} ui′则是节点 v i v_{i} vi作为邻居时所表达出的一个"上下文"向量。
( u i u_{i} ui. u j ′ u^{'}_{j} uj′)的点乘就表达了节点 V i V_{i} Vi本身与节点 V j V_{j} Vj的邻居之间的关系,也就是公式(5)当中的分子部分。公式(5)中|v|表示网络结构中所有的点,其实算是一个softmax函数,它代表了节点 V i V_{i} Vi本身与节点 V j V_{j} Vj的邻居之间的关系在节点 V i V_{i} Vi与网络结构中所有的其它节点的邻居之间关系的占比。
这样,原问题就又转换成了度量公式(5)与公式(6)之间距离的问题。目标函数定义如公式(7)所示,其中 λ i λ_{i} λi表示节点 V i V_{i} Vi的重要程度,文中假设度比较高的节点权重较高,令 λ i = d i λ_{i}=d_{i} λi=di,还是采用KL散度度量公式(5)与公式(6)分布之间的距离,省去常数项后得到如公式(8)所示的优化目标函数。但,直接去迭代公式(8)的计算代价很大。因此,还是采用Negative sampling的方式进行负采样,得到二阶近邻的优化目标,如公式(9)所示。
2.3.其它优化
注意到不管在一阶近邻目标函数公式(4)还是二阶近邻目标函数(9)当中都存在权重系数 w i j w_{ij} wij,在梯度下降的过程中, w i j w_{ij} wij是一个常数,如果过大会导致学习率的选择变得困难,而较大的学习率又会导致梯度爆炸的问题,较小的学习率又会导致学习速度过慢,陷入局部最优解当中。
如果所有边的权重相同,则上述问题就可以得到很好的解决,所以我们在这里可以对所有的带权边进行采样,被采样的概率等价于其权重,这样就解决了学习率的问题。采样算法采用Alias算法,该算法的具体内容可以参考博客
https://zhuanlan.zhihu.com/p/54867139
3.其它问题
3.1 低度数顶点
对于一些顶点由于其邻接点非常少会导致embedding向量的学习不充分,论文提到可以利用邻居的邻居构造样本进行学习,这里也暴露出LINE方法仅考虑一阶和二阶相似性,对高阶信息的利用不足。
3.2 新加入顶点
对于新加入图的顶点 ,若该顶点与图中顶点存在边相连,我们只需要固定模型的其他参数,优化如下两个目标之一即可:
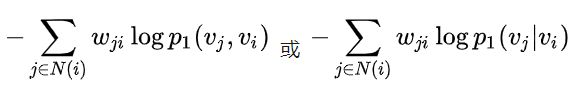
4.参考博客
LINE算法原文
https://arxiv.org/pdf/1503.03578.pdf
435算法研究所
https://zhuanlan.zhihu.com/p/74746503
浅梦
https://zhuanlan.zhihu.com/p/56478167
浅梦的LINE算法实现代码
https://github.com/shenweichen/GraphEmbedding